
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Проектирование эвольвентного зубчатого зацепленияСодержание книги Похожие статьи вашей тематики
Поиск на нашем сайте
6.1 Геометрические размеры зацепления
Подавляющее большинство механизмов предназначено для преобразования вращательного движения начального звена во вращательное движение других звеньев с постоянным передаточным отношением. Этого достигают соответствующим выбором геометрии соприкасающихся элементов высшей пары. Взаимодействующие поверхности элементов высшей пары, обеспечивающие заданный закон относительного движения звеньев, называются сопряженными поверхностями. Чтобы воспроизвести непрерывное вращательное движение в одном направлении, надо иметь замкнутую систему сопряженных поверхностей (профилей), расположенных на выступах, называемых зубьями. Высшая кинематическая пара, образуемая замкнутой системой последовательно взаимодействующих сопряженных поверхностей (профилей), называется зубчатым зацеплением. Синтез зацепления состоит в отыскании геометрии сопряженных поверхностей (профилей) по заданному закону их относительного движения. В эвольвентных зубчатых колесах профили зубьев очерчиваются по эвольвентам окружности с центром на оси колеса. Геометрическое место центров кривизны какой- либо кривой называется эволютой, а сама кривая по отношению к эволюте - разверткой или эвольвентой. Следовательно, эвольвента окружности есть кривая, центры кривизны которой лежат на окружности. Эвольвента (для краткости в дальнейшем опускаем слово «окружности») может быть получена как траектория точки прямой, перекатывающейся без скольжения по окружности. В теории зацепления окружность, эвольвентой которой является профиль зуба, называется основной окружностью. На рис. 6.1 показано построение эвольвенты основной окружности Обозначим через
Рис. 6.1
Выразим длину делительной окружности
где Окружной шаг Делительную окружность можно определить как окружность, для которой модуль имеет стандартную величину, или же как окружность, которая является базовой для определения размеров зубьев. Делительная окружность диаметра Различают внешние (рис. 6.2, а) и внутренние (рис. 6.2, б) зубья. У внешних зубьев окружность вершин находится снаружи окружность впадин, а у внутренних- внутри окружность впадин. Высота головки обозначаемся через
Рис. 6.2
Толщина зуба
Или Модуль Размеры зубчатых передач, составленных из колес, в которых делительные и начальные окружности совпадают, определяются следующими формулами:
Нижние знаки в формулах (6.2) относятся к колесам с внутренними зубьями (рис. 6.2, б).
6.2 Построение картины эвольвентного зацепления для нормальных колес Известны: модуль и число зубьев колес z1 и z2. Требуется построить внешнее эвольвентное зацепление. По формулам (6.1-6.2) подсчитываем размеры зубчатых передач. Для колеса 1- шестерни- обозначаем параметры с индексом 1, для колеса 2 – с индексом 2 (d1, d2; da1; da2; df1, df2). Для наглядности картины эвольвентного зацепления необходимо выбрать такой масштаб, чтобы высота зуба на чертеже была не меньше 50 мм. Определяем масштаб построения Пересчитываем все размеры с учетом масштаба. Откладываем межосевое расстояние aw = О1О2, из центров О1 и О2 проводим окружности радиусами В нашем случае начальные и делительные окружности совпадают (так как мы проектируем зубья колес без смещения). Но при этом надо иметь в виду их принципиальное отличие. Делительная окружность есть характеристика зубчатого колеса и диаметр ее постоянен. Начальные окружности дают характеристику зацепления двух зубчатых колес, и диаметры этих окружностей зависят от межосевого расстояния. Проводим окружности вершин и впадин зубьев по найденным размерам (рис. 6.3).
Рис. 6.3
Точка Р касания начальных окружностей будет полюсом зацепления, т.е. через нее должны проходить все общие нормали, проведенные через точки касания эвольвентных профилей. По третьему свойству нормаль эвольвенты пересекает окружность, концентрическую основной, под постоянным углом. Так как центры основных окружностей будут располагаться в центрах О1 и О2 вращения зубчатых колес, то начальные окружности являются концентрическими по отношению к основным. Следовательно, производящая прямая должна проходить через полюс Р зацепления и пересекать начальные окружности под углом зацепления, равным 200. Углом зацепления От общей касательной Отрезок N1N2 является геометрическим местом точек контакта сопряженных профилей и называется теоретической линией зацепления. Действительная линия зацепления представляет собой отрезок прямой, заключенный между началом и концом зацепления. Начало и конец зацепления (точки a и b) – это точки пересечения окружностей вершин зубьев с линией зацепления. Так как производящая прямая должна быть касательна к основным окружностям, то радиусы основных окружностей rb1 и rb2 –это длины перпендикуляров О1N1 и О2N2. Из центров О1 и О2 проводим дуги основных окружностей. Профили зубьев очерчиваются по эвольвентам. Чтобы вычертить эвольвенту, надо иметь основную окружность, производящую прямую и чертящую точку на ней. Обычно за чертящую точку берется полюс зацепления Р. При перекатывании производящей прямой N1Р по первой основной окружности (радиуса rb1) получается эвольвента (профиль зуба) первого колеса, при перекатывании производящей прямой N2Р по второй основной окружности (радиуса rb2) получается эвольвента (профиль зуба) второго колеса. Профили зубьев должны быть от окружности вершин зубьев до окружности впадин, но эвольвента идет только до основной окружности.
Если число зубьев больше 41, то радиус основной окружности меньше радиуса окружности впадин, и весь профиль зуба может быть очерчен по эвольвенте. Если же z < 41, то радиус основной окружности больше радиуса окружности впадин и только часть профиля зуба получается эвольвентной. Для построения эвольвенты отрезок РN2 разбиваем на четыре равные части и из точки 3 радиусом 3 -Р проводим дугу до пересечения с основной окружностью в точке Р1. В этом случае дуга N2Р1 равна отрезку N2Р. После этого на прямой РN2 вниз от точки N2 откладываем отрезки Дугу N2Р1 делим на 4 равные части, обозначаем точками Соединяя последовательно точки Участок профиля зуба, заключенный между основной окружностью и окружностью впадин, будет нерабочим. В этом случае эвольвенту продолжают по прямой (по радиусу) и делают закругление (галтель) радиусом ρf = 0,38 m, соединяющее профиль зуба с окружностью впадин. Если от полюса зацепления по начальной окружности отложим расстояние, равное четверти шага
Рис. 6.4
Не все участки профилей зубьев взаимодействуют друг с другом. Профиль головки зуба полностью участвует в зацеплении и работает по ножке сопряженного зуба. Профиль же ножки зуба не весь участвует в зацеплении. Тот участок профиля, на котором происходит фактическое касание сопряженных зубьев, называется активным.
Чтобы определить границу активного участка профиля, нужно на ножке зуба найти точку, сопряженную с вершиной парного зуба. Следовательно, чтобы найти активные участки профилей зубьев обоих колес, нужно через начало и конец зацепления (через точки a и b) провести дуги: из центра О1 радиусом О1 а до встречи с профилем зуба в точке а1, а через точку b из центра О2 радиусом О2 b до встречи со своим профилем зуба в точке b2. На рисунке 6.5 активные участки профилей заштрихованы. Путь, пройденный любой точкой начальной окружности за время зацепления одной пары сопряженных зубьев называется дугой зацепления. Длина дуги зацепления равна длине дуги начальной окружности, заключенной между профилями зуба, проведенными через начало и конец зацепления (через точки а и b).
6.3 Качественные показатели зубчатой передачи
Свойства спроектированной зубчатой передачи характеризуются ее качественными показателями, главнейшим из которых является коэффициент перекрытия. Для нормальной работы зубчатого зацепления длина дуги должна быть больше шага. Если дуга зацепления будет меньше шага, то в таком зацеплении будут происходить перерывы, а, следовательно, и удары, что недопустимо. Если дуга зацепления будет точно равна шагу, то следующая пара зубьев будет сцепляться в тот момент, когда предыдущая пара расцепляется. Такое зацепление тоже нежелательно, необходимо хоть небольшое перекрытие. Поэтому дуга зацепления должна быть больше шага. Коэффициент перекрытия характеризует такие важнейшие свойства процесса зацепления, как его непрерывность и продолжительность. Отношение дуги зацепления к шагу зацепления называется коэффициентом перекрытия
Для внешнего зацепления коэффициент перекрытия колеблется в пределах e = 1,2 – 1,8. Для аналитического расчета этого коэффициента следует длину действительной линии зацепления выразить через основные размеры зубчатых колес. После преобразований получим окончательную формулу для определения коэффициента перекрытия при внешнем зацеплении:
Коэффициент удельного давления учитывает влияние геометрии зубьев (радиусов кривизны их профилей) на величину контактных напряжений, возникающих в местах соприкосновения зубов. Чем больше радиусы кривизны, тем меньше контактные напряжения. Коэффициент контактного напряжения
где
Используя третье свойство эвольвенты, запишем формулу коэффициента удельного скольжения для момента зацепления, когда зубья соприкасаются в полюсе Р:
Коэффициенты скольжения учитывают влияние геометрических и кинематических факторов на величину проскальзывания профилей в процессе их зацепления. Чем интенсивнее проскальзывание, тем значительнее износ зубьев.
Коэффициент скольжения
Рис. 6.6
Тогда расчетные формулы применительно к внешнему эвольвентному зацеплению примут вид:
|
|||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-06-23; просмотров: 989; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.12.196.93 (0.013 с.) |

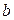 при перекатывании по ней прямой
при перекатывании по ней прямой  , называемой производящей прямой.
, называемой производящей прямой. острый угол между касательной
острый угол между касательной  к эвольвенте и радиусом- вектором эвольвенты ОМ. В теории эвольвентного зацепления он называется углом профиля. Угол, образованный начальным радиусом – вектором эвольвенты ОМ0 и ее текущим радиусом ОМ, называется эвольвентным углом и обозначается через
к эвольвенте и радиусом- вектором эвольвенты ОМ. В теории эвольвентного зацепления он называется углом профиля. Угол, образованный начальным радиусом – вектором эвольвенты ОМ0 и ее текущим радиусом ОМ, называется эвольвентным углом и обозначается через  . Кроме того, обозначим через
. Кроме того, обозначим через  радиус основной окружности.
радиус основной окружности.
 через число зубьев колеса
через число зубьев колеса  :
:  , где
, где  - окружной шаг, т. е. расстояние, измеренное по дуге окружности диаметра
- окружной шаг, т. е. расстояние, измеренное по дуге окружности диаметра  между двумя соответствующими точками соседних зубьев. Отсюда
между двумя соответствующими точками соседних зубьев. Отсюда или
или  (6.1),
(6.1), - отношение окружного шага к числу
- отношение окружного шага к числу  , называемое модулем зуба.
, называемое модулем зуба. и модуль
и модуль  для одного и того же зуба зависят от диаметра окружности, к которой они относятся.
для одного и того же зуба зависят от диаметра окружности, к которой они относятся. (рис. 6.2) делит зуб на две части: головку и ножку. Делительной головкой (сокращенно – головкой) зуба называется часть зуба, расположенная между делительной окружностью и окружностью вершин, диаметр которой обозначается через
(рис. 6.2) делит зуб на две части: головку и ножку. Делительной головкой (сокращенно – головкой) зуба называется часть зуба, расположенная между делительной окружностью и окружностью вершин, диаметр которой обозначается через  . Делительной ножкой (сокращенно - ножкой) зуба называется часть зуба, расположенная между делительной окружностью и окружностью впадин, диаметр которой обозначается через
. Делительной ножкой (сокращенно - ножкой) зуба называется часть зуба, расположенная между делительной окружностью и окружностью впадин, диаметр которой обозначается через  . Допускается также применение терминов «начальная головка» и «начальная ножка», если зуб делится по высоте не делительной, а начальной окружностью.
. Допускается также применение терминов «начальная головка» и «начальная ножка», если зуб делится по высоте не делительной, а начальной окружностью. , высота ножки – через -
, высота ножки – через -  , общая высота зуба – через
, общая высота зуба – через  . Высота ножки больше высоты головки, так как между окружностью вершин зубьев одного колеса и окружностью впадин зубьев другого колеса должен быть зазор, называемый радиальным зазором. Каждый зуб очерчен двумя симметрично расположенными профилями. Расстояние между этими профилями, измеренное по какой- либо окружности, называется толщиной зуба. Толщина зуба по делительной окружности обозначается через
. Высота ножки больше высоты головки, так как между окружностью вершин зубьев одного колеса и окружностью впадин зубьев другого колеса должен быть зазор, называемый радиальным зазором. Каждый зуб очерчен двумя симметрично расположенными профилями. Расстояние между этими профилями, измеренное по какой- либо окружности, называется толщиной зуба. Толщина зуба по делительной окружности обозначается через  .
.
 по делительной окружности равна половине шага зацепления
по делительной окружности равна половине шага зацепления

 , в долях которого определяются размеры исходного контура, выбирают из стандартного ряда модулей. Остальные параметры по ГОСТ 13754-68 и СТ СЭВ 308-76 имеют следующие значения: угол профиля
, в долях которого определяются размеры исходного контура, выбирают из стандартного ряда модулей. Остальные параметры по ГОСТ 13754-68 и СТ СЭВ 308-76 имеют следующие значения: угол профиля  , коэффициент радиального зазора
, коэффициент радиального зазора  , радиус закругления
, радиус закругления  .
.





 (6.2)
(6.2)




 .
. и
и  , называемые начальными. Они представляют собой геометрическое место точек, по которым звенья друг по другу перемещаются без скольжения.
, называемые начальными. Они представляют собой геометрическое место точек, по которым звенья друг по другу перемещаются без скольжения.
 называется угол между линией зацепления и прямой, перпендикулярной межосевой линии.
называется угол между линией зацепления и прямой, перпендикулярной межосевой линии. начальных окружностей отложим угол зацепления a = 200 и проведем линию зацепления. Из центров вращения зубчатых колес О1 и О2 опустим перпендикуляры О1N1 и О2N2 на линию зацепления. Получим прямую N1N2 - производящую прямую.
начальных окружностей отложим угол зацепления a = 200 и проведем линию зацепления. Из центров вращения зубчатых колес О1 и О2 опустим перпендикуляры О1N1 и О2N2 на линию зацепления. Получим прямую N1N2 - производящую прямую. и
и  , равные отрезку
, равные отрезку  (рис. 6.4).
(рис. 6.4). ,
,  ,
,  ,
,  , откладываем вниз от точки N2 точки
, откладываем вниз от точки N2 точки  и
и  . Соединяем все шесть полученных точек с центром О2. Из точек
. Соединяем все шесть полученных точек с центром О2. Из точек  ,
,  , …,
, …,  (или касательные к основной окружности в точках
(или касательные к основной окружности в точках  ,
,  ,
,  ,
,  ,
,  , соответственно равные отрезкам 1P, 2P, 3P, 5Р, 6Р.
, соответственно равные отрезкам 1P, 2P, 3P, 5Р, 6Р. ,
,  ,
,  , Р,
, Р, 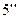 ,
,  плавной кривой, получим эвольвенту для первого колеса.
плавной кривой, получим эвольвенту для первого колеса. , то найдем ось симметрии зуба. Проводим оси симметрии обоих зубьев и относительно этих осей строим профили, симметричные только что вычерченным. Отложив от оси симметрии зуба по начальной окружности шаг зацепления р, получим ось симметрии следующего зуба. Имея ось симметрии зуба, нетрудно построить второй зуб. Обычно при построении зубчатого зацепления вычерчивают по три зуба на каждом зубчатом колесе (рис. 6.5).
, то найдем ось симметрии зуба. Проводим оси симметрии обоих зубьев и относительно этих осей строим профили, симметричные только что вычерченным. Отложив от оси симметрии зуба по начальной окружности шаг зацепления р, получим ось симметрии следующего зуба. Имея ось симметрии зуба, нетрудно построить второй зуб. Обычно при построении зубчатого зацепления вычерчивают по три зуба на каждом зубчатом колесе (рис. 6.5).

 (6.3)
(6.3) (6.4)
(6.4) (6.5)
(6.5) - приведенный радиус кривизны эвольвентных профилей в точке К контакта, определяемый как
- приведенный радиус кривизны эвольвентных профилей в точке К контакта, определяемый как .
.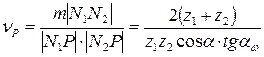 (6.6)
(6.6) шестерни 1 принято подсчитывать для того момента зацепления, когда зубья соприкасаются в точке
шестерни 1 принято подсчитывать для того момента зацепления, когда зубья соприкасаются в точке  , т. е. когда в зацеплении находится ножка зуба шестерни; коэффициент скольжения
, т. е. когда в зацеплении находится ножка зуба шестерни; коэффициент скольжения  колеса 2 – когда зубья соприкасаются в точке
колеса 2 – когда зубья соприкасаются в точке  , т. е. когда в зацеплении находится ножка зуба колеса (рис. 6.6).
, т. е. когда в зацеплении находится ножка зуба колеса (рис. 6.6).
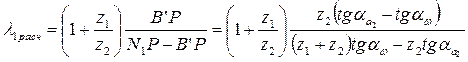 (6.7)
(6.7) (6.8)
(6.8)


