
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
К выполнению курсового проектаСодержание книги Поиск на нашем сайте К ВЫПОЛНЕНИЮ КУРСОВОГО ПРОЕКТА ПО ДИСЦИПЛИНЕ „ТЕОРИЯ МЕХАНИЗМОВ И МАШИН” (для студентов специальностей 7.090214 “Подъемно- транспортные, строительные, дорожные, мелиоративные машины и оборудование” и 7.090258 „Автомобили и автомобильное хозяйство” очной формы обучения)
Утверждено на заседании кафедры «Подъемно- транспортные, строительные, дорожные машины и оборудование» Протокол № 2 от 22.09.2006 г.
Макеевка 2006
УДК 621.01
Методические указания к выполнению курсового проекта по дисциплине «Теория механизмов и машин» (для студентов специальностей 7.090214 “Подъемно- транспортные, строительные, дорожные, мелиоративные машины и оборудование” и 7.090258 „Автомобили и автомобильное хозяйство” очной формы обучения) / Сост.: В.П. Мельник, Н.А. Юрченко, А.Н. Клен – Макеевка: ДонНАСА, 2006. – 112 с.
В методических указаниях даны теоретические предпосылки и примеры решения задач, составляющих содержание курсового проекта.
Составители: доц. В.П. Мельник асс. Н.А. Юрченко асс. А.Н. Клен
Рецензенты: доц. А.В. Гаврюков доц. Т.В. Луцко
Ответственный за выпуск: проф. В.А. Пенчук
СОДЕРЖАНИЕ 1 Структурный анализ механизмов……………………………………5 1.1 Общие понятия………………………… 5 1.2 Классификация кинематических пар, кинематических цепей механизмов………………………………………… 7 1.3 Число степеней свободы механизма 10 1.4 Принцип Ассура структурного строения и образования плоских рычажных механизмов 11 2 Кинематический анализ плоских рычажных механизмов 16 2.1 Общие понятия 16 2.2 Траектории и разметка траекторий точек механизмов 16 2.3 Построение плана скоростей и ускорений для плоского рычажного механизма 18 2.4 Особенности построения плана скоростей и ускорений для кулисного механизма 25 2.5 Построение кинематических диаграмм для выходного звена 30 3. Силовой анализ механизма 34 3.1 Общие сведения 34 3.2 Пример силового расчета 36 3.2.1 Расчет структурной группы, состоящей из звеньев 4 и 5 37 3.2.2 Расчет структурной группы, состоящей из звеньев 2 и 3 41 3.2.3 Расчет начального звена 45 3.3 Определение уравновешивающей силы методом рычага Жуковского 48 3.4 Особенности кинетостатического анализа для кулисного механизма 51 4 Динамический синтез маховика 54 4.1 Определение момента инерции маховика 54 4.2 Определение геометрических размеров маховика 65 5. Расчет кулачковых механизмов 67 5.1 Общие понятия 67 5.2 Анализ и синтез кулачковых механизмов 69 5.2.1 Центральный кулачковый механизм, в котором кулачок работает по толкателю с острием 69 5.2.2 Дезаксиальный кулачковый механизм, в котором кулачок работает по толкателю с острием 72 5.2.3 Центральный кулачковый механизм, в котором кулачок работает по толкателю с роликом 74 5.2.4 Дезаксиальный кулачковый механизм, в котором кулачок перемещает толкатель с роликом 75 5.2.5 Кулачковый механизм, в котором кулачок перемещает плоский толкатель 76 5.2.6 Кулачковый механизм, в котором кулачок перемещает коромысло с острием 78 5.2.7 Кулачковый механизм, в котором кулачок перемещает коромысло с роликом 80 5.2.8 Кулачковый механизм, в котором кулачок работает по плоскому колебателю 81 6 Проектирование эвольвентного зубчатого зацепления 84 6.1 Геометрические размеры зацепления 84 6.2 Построение картины эвольвентного зацепления для нормальных колес 87 6.3 Качественные показатели зубчатой передачи 92 7 Проектирование сложного зубчатого зацепления 94 7.1 Общие сведения 94 7.2 Механизмы многоступенчатых зубчатых передач с неподвижными осями (параллельными и пересекающимися) 97 7.3 Механизмы многоступенчатых передач с подвижными осями 99 7.4 Синтез планетарных механизмов 103 Список литературы 111
Силовой анализ механизма
3.1 Общие сведения
Во время движения механизма в его кинематических парах действуют силы, являющиеся силами взаимодействия между звеньями. Знание сил в кинематических парах необходимо для расчета звеньев механизма на прочность, жесткость, вибростойкость, износоустойчивость. Определение сил в кинематических парах, а также неизвестных внешних сил, приложенных к механизму, составляет содержание силового расчета механизмов. Силовой расчет основан на методах кинетостатики. Кинетостатика - это раздел механики, который позволяет с помощью принципа Даламбера и принципа освобождаемости от связей придать задаче динамики форму задачи статики. Иными словами, рассмотрение условного равновесия механизма позволяет определить искомые силы. Принцип Даламбера: при движении механической системы активные силы, реакции связей и силы инерции образуют равновесную систему сил в любой момент движения
где
Как известно, при плоском движении тела его инерция сводится к главному вектору сил инерции и главному моменту сил инерции. Так, например, для звена АВ, движущегося плоскопараллельно (рис. 3.1), инерция приводится к двум величинам: а) сила инерции
где
Рис. 3.1
Как следует из уравнения (3.1), главный вектор сил инерции б) момент сил инерции
где В случае, если звено АВ – стержень с равномерно распределенной массой,
Главный момент сил инерции направлен противоположно угловому ускорению звена. На выходное звено действует сила (момент) полезного сопротивления. Полезными сопротивлениями называют усилия, для преодоления которых и предназначен механизм или машина. Силы и моменты сил полезного сопротивления всегда направлены противоположно движению (скорости). Принцип освобождаемости от связей - не нарушая движения или покоя системы, можно отбрасывать отдельные связи и прикладывать к системе соответствующие этим связям реакции. Так, например, во вращательной кинематической паре (цилиндрический шарнир) реакция связи
Рис. 3.2
В поступательной кинематической паре в случае отсутствия трения реакция Реакции связей для низших кинематических пар содержат две неизвестные величины: а) модули
Уравнение (3.3) полностью совпадает с условием группы Ассура. Таким образом, группы Ассура являются статически определимыми системами. Тогда силовой расчет механизма состоит в последовательном рассмотрении равновесия групп Ассура с определением неизвестных реакций связи. При этом порядок силового расчета - обратный по сравнению с кинематическим расчетом, т.е. вначале рассматривается последняя присоединенная структурная группа. Рассмотрим суть силового расчета, основанного на методах кинетостатики, на конкретном примере.
3.2 Пример силового расчета
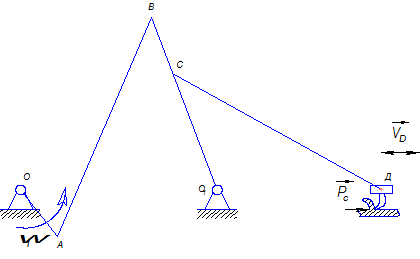
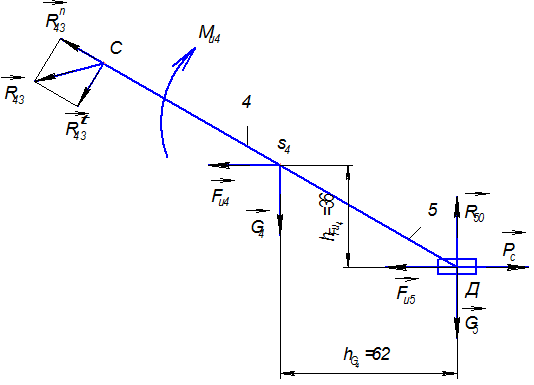
Пусть имеется строгальный станок, кинематическая схема которого указана на рис. 3.3. Исходные данные: Длины звеньев: ½ОА½=0,12м, ½АВ½=0,5 м, ½ВО1½=0,4 м, ½ВС½=0,15 м, ½ДС½=0,5 м; погонная масса звеньев Начальное звено 1 (кривошип) движется равномерно с постоянной угловой скоростью w1=10 рад/с. Из плана ускорений: угловые ускорения звеньев:
На выходное звено действует сила полезного сопротивления
Рис. 3.3
Необходимо определить реакции в кинематических парах, а также уравновешивающую силу, приложенную к начальному звену.
Для решения задачи разобъем механизм на структурные группы (рис. 3.4).
Рис. 3.4
3.2.1 Расчет структурной группы, состоящей из звеньев 4 и 5
Силовой расчет начнем с рассмотрения последней группы, присоединенной к механизму. При этом воспользуемся принципом Даламбера и принципом освобождаемости от связей. Вычерчиваем структурную группу (рис. 3.5), состоящую из звеньев 4 и 5 в масштабе а) активные: сила сопротивления Масса звеньев
Силы тяжести
Рис. 3.5
б) реакции связей: в) силы и моменты сил инерции: Fu4= m4 as4= Fu5= m5 as5=
Составляем векторное уравнение равновесия всех сил для структурной группы:
Уравнение (3.4) содержит три реакции, неизвестные по величине, но известные по направлению: Составим уравнение моментов сил, действующих на звено 4, относительно точки Д:
Отсюда найдем, что реакция
Все плечи сил, входящих в уравнение, определяем из чертежа структурной группы с учетом масштаба (измеряем на чертеже в мм, в формулу подставляем уже в м):
Знак «минус» указывает, что в действительности реакция Реакции План сил представляет собой векторное изображение сил, выполненное в масштабе. Задаемся масштабом плана сил mР= 10 Н/мм (масштаб выбираем такой, чтобы наибольшая по модулю сила не превышала 100-120 мм на чертеже). Вычисляем величины отрезков, которые будут отображать векторы уравнения (3.4) на плане сил:
Построение начнем с полюса Р, из которого отложим вначале вектор
Рис. 3.6
Чтобы выполнялось условие равновесия, силовой многоугольник, построенный по уравнению (3.4), должен быть замкнутым. Следовательно, мы должны провести из полюса направление одного неизвестного по величине вектора (
Для определения реакции связи
В этом уравнении неизвестен только вектор
3.2.2 Расчет структурной группы, состоящей из звеньев 2 и 3
Вычерчиваем структурную группу (рис. 3.7), состоящую из звеньев 2 и 3 в масштабе
Рис. 3.7
а) активные: силы тяжести звеньев Масса звеньев
Силы тяжести
б) реакции связей: в) силы и моменты сил инерции: Fu2= m2 as2= Fu3= m3 as3=
В точке С будет действовать реакция
Рассмотрев равновесие каждого звена (2 и 3) в отдельности в форме моментов сил относительно точки В, определим тангенциальные реакции
Отсюда, Все плечи сил, входящих в уравнение, определяем из чертежа структурной группы с учетом масштаба:
Отсюда, Все плечи сил, входящих в уравнение, определяем из чертежа структурной группы с учетом масштаба:
Реакции
В этом уравнении неизвестны по величине только искомые векторы Задаемся масштабом плана сил mР= 6 Н/мм. Вычисляем величины отрезков, которые будут отображать векторы уравнения (3.10) на плане сил:
Построение начнем с полюса Р, из которого отложим вначале вектор
Рис. 3.8
Силовой многоугольник, построенный по уравнению (3.10), должен быть замкнутым. Следовательно, проводим из полюса направление одного неизвестного по величине вектора (
Для определения реакции связи между звеньями
В этом уравнении неизвестен только вектор
3.2.3 Расчет начального звена
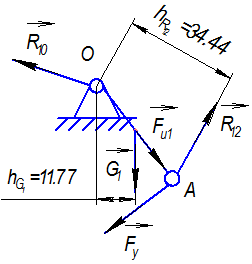
Перейдем к расчету начального звена. Приложим к начальному звену действующие на него реакции связей, активные силы и силы инерции (рис. 3.9). Учтем при этом, что
(направление реакции берем из предыдущего плана сил). Масса начального звена
Сила тяжести
Сила инерции звена:
Рис. 3.9
В точке О прикладываем реакцию Поскольку ведущее звено имеет одну степень свободы, то это обстоятельство учитывается путем приложения дополнительной силы
Плечи сил, входящих в уравнение, определяем из чертежа структурной группы с учетом масштаба:
Тогда уравновешивающий момент
Уравновешивающий момент равен необходимому вращающему моменту, который должен быть приложен со стороны двигателя, чтобы механизм двигался с заданной скоростью, преодолевая заданную нагрузку. Направления Реакция
Задаемся масштабом плана сил mР= 20 Н/мм. Вычисляем величины отрезков, которые будут отображать векторы уравнения (3.13) на плане сил:
Рис. 3.10
Построение начнем с полюса Р (рис. 3.10). Векторы
Искомая реакция
3.3 Определение уравновешивающей силы методом рычага Жуковского Если для механизма построен план скоростей, повернутый на 90о, то, найдя скорости точек приложения внешних сил, можно к концам найденных векторов скоростей приложить действующие внешние силы. После этого, рассматривая повернутый план скоростей как жесткий рычаг, вращающийся вокруг полюса Р, можно написать уравнение равновесия рычага в виде суммы моментов сил относительно полюса. Из уравнения легко определяется уравновешивающая сила Если к звеньям механизма приложены, кроме сил, еще и моменты, то каждый из них можно рассматривать как пару сил, составляющая
где
Рис. 3.11
Найденные силы прикладываются в соответствующих точках плана скоростей. При определении уравновешивающей силы можно поворачивать на 90о не план скоростей, а все внешние силы, приложенные к звеньям механизма, при переносе их на план скоростей. При этом все силы должны быть повернуты в одну и ту же сторону. Пример. План скоростей (для положения, которое мы брали для силового расчета) поворачиваем в любую сторону на 900 (рис. 3.12, а). Масштаб берем произвольный. Переносим все заданные силы, действующие в рассматриваемый момент времени на звенья механизма (силы тяжести, силы инерции, силу полезного сопротивления, уравновешивающую силу) в одноименные точки повернутого плана скоростей, не изменяя при этом направления этих сил (рис. 3.12, б). Моменты заменяем парой сил, вычисляем значение сил:
Составляем уравнение моментов всех перенесенных сил относительно полюса плана скоростей
Из уравнения (3.15) определяем уравновешивающую силу
Подставим значения в формулу. Значения плеч сил подставляем, не умножая на масштаб (масштаб выносится из всех слагаемых за скобки и сокращается).
Рис. 3.12
3.4 Особенности кинетостатического анализа для кулисного механизма
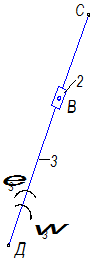
На рис 3.13 изображена схема кулисного механизма. Силовой расчет для структурной группы, состоящей из звеньев 4 и 5, проводится, как описано в п. 3.2.1.
В результате расчета определяем величину и направление реакции
Рис. 3.13
Рассмотрим структурную группу, состоящую из звеньев 2 и 3 (рис. 3.14).
Рис. 3.14 Вычертим отдельно звено 3 (рис. 3.15, а) и приложим к нему: -силу тяжести -силу инерции -реакцию -момент сил инерции -реакцию -реакцию
Рис. 3.15
Определим величину реакции
Отсюда,
Запишем силы, действующие на звено 3:
Задаемся масштабом плана сил Строим план сил (рис. 3.15, б). Определяем величину реакции Рассмотрим силы, действующие на камень (рис. 3.16, а):
Сила тяжести Сила инерции Реакция Построим план сил (рис. 3.16, б).
Рис. 3.16
Определяем величину реакции Расчет начального звена аналогичен приведенному ранее примеру.
СПИСОК ЛИТЕРАТУРЫ
1. Артоболевский И.И. Теория механизмов и машин. – М.: Наука, 1988. – 638 с. 2. Левитский Н.И. Теория механизмов и машин: Учеб. пособие для вузов. – 2-е изд., перераб. и доп. – М.: Наука, Гл. ред. физ.-мат. лит., 1990. – 592 с. 3. Озол О.Г. Теория механизмов и машин. – М.: Наука, 1984. – 432 с. 4. Попов С.А. Курсовое проектирование по теории механизмов и механике машин: Учеб. пособие для втузов / С.А. Попов, Г.А. Тимофеев; Под ред. К.В. Фролова. – 4-е изд., перераб. и доп. – М.: Высш. шк., 2002. – 411 с. 5. Теория механизмов и механика машин: Учеб. для втузов / К.В. Фролов, С.А. Попов, А.К. Мусатов и др.; Под ред. К.В. Фролова. – 3-е изд., стер. – М.: Высш. шк., 2001. – 496 с. Учебное издание МЕТОДИЧЕСКИЕ УКАЗАНИЯ ПО ДИСЦИПЛИНЕ „ТЕОРИЯ МЕХАНИЗМОВ И МАШИН” (для студентов специальностей 7.090214 “Подъемно- транспортные, строительные, дорожные, мелиоративные машины и оборудование” и 7.090258 „Автомобили и автомобильное хозяйство” очной формы обучения)
Составители: МЕЛЬНИК Владимир Порфирьевич ЮРЧЕНКО Наталья Андреевна КЛЕН Андрей Николаевич
|
||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-06-23; просмотров: 370; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.102 (0.008 с.) |





 ,
,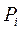 -
- 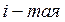 активная сила;
активная сила;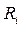 -
-  -
-  (3.1)
(3.1)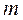 - масса звена АВ, кг;
- масса звена АВ, кг; -ускорение центра масс этого звена, м/с2.
-ускорение центра масс этого звена, м/с2.
 направлен противоположно ускорению
направлен противоположно ускорению  (прикладывается в центре масс звена).
(прикладывается в центре масс звена). (3.2)
(3.2)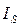 - момент инерции звена относительно оси, проходящей через центр масс s.
- момент инерции звена относительно оси, проходящей через центр масс s. ,
,  .
. - угловое ускорение звена АВ,
- угловое ускорение звена АВ,  .
. в случае отсутствия трения проходит через центр вращения О. Обычно эту реакцию раскладывают на две составляющие: нормальную
в случае отсутствия трения проходит через центр вращения О. Обычно эту реакцию раскладывают на две составляющие: нормальную  , направленную вдоль звена, и касательную
, направленную вдоль звена, и касательную 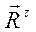 , направленную перпендикулярно звену (рис. 3.2, а).
, направленную перпендикулярно звену (рис. 3.2, а).
 направлена перпендикулярно траектории движения ползуна (рис. 3.2, б).
направлена перпендикулярно траектории движения ползуна (рис. 3.2, б). и
и  для вращательной кинематической пары; б) модуль и линию действия (точку приложения)
для вращательной кинематической пары; б) модуль и линию действия (точку приложения)  для поступательной кинематической пары. Следовательно, общее число неизвестных связей в механизме будет равно
для поступательной кинематической пары. Следовательно, общее число неизвестных связей в механизме будет равно  , где
, где 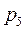 - число низших кинематических пар (5 класс). Для каждого звена можно записать 3 уравнения равновесия. Следовательно, для
- число низших кинематических пар (5 класс). Для каждого звена можно записать 3 уравнения равновесия. Следовательно, для  звеньев механизма число уравнений равновесия равно
звеньев механизма число уравнений равновесия равно  . Тогда условие статической определимости для всего механизма будет иметь вид:
. Тогда условие статической определимости для всего механизма будет иметь вид: (3.3)
(3.3)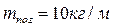 .
. ;
;  ;
; 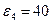 рад/с2; ускорения центров масс звеньев:
рад/с2; ускорения центров масс звеньев: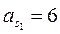 м/с2;
м/с2; 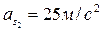 ;
;  ;
;  м/с2,
м/с2,  м/с2
м/с2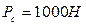 .
.

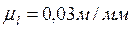 (масштаб можно взять такой, как при вычерчивании планов механизма). Тогда к звеньям 4-5 будут приложены следующие силы:
(масштаб можно взять такой, как при вычерчивании планов механизма). Тогда к звеньям 4-5 будут приложены следующие силы: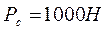 и силы тяжести звеньев
и силы тяжести звеньев  и
и  , приложенные в центрах тяжести.
, приложенные в центрах тяжести.

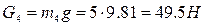

 для поступательной пары 5-0, приложенная перпендикулярно траектории движения ползуна Д;
для поступательной пары 5-0, приложенная перпендикулярно траектории движения ползуна Д; 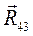 для вращательной пары 4-3, которую разложим на две составляющие: нормальную
для вращательной пары 4-3, которую разложим на две составляющие: нормальную  (направим её параллельно звену 4) и тангенциальную
(направим её параллельно звену 4) и тангенциальную 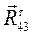 (направим её перпендикулярно этому звену);
(направим её перпендикулярно этому звену);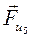 , направленная противоположно ускорению точки Д,
, направленная противоположно ускорению точки Д,  , направленная противоположно ускорению
, направленная противоположно ускорению 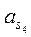 (см. план ускорений) и момент
(см. план ускорений) и момент 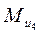 , направленный противоположно угловому ускорению
, направленный противоположно угловому ускорению  . При этом
. При этом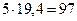 Н
Н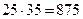 Н
Н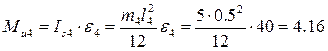 Нм.
Нм. (3.4)
(3.4)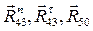 . Чтобы по уравнению (3.4) можно было построить силовой многоугольник (план сил), необходимо определить величину хотя бы одной из неизвестных реакций.
. Чтобы по уравнению (3.4) можно было построить силовой многоугольник (план сил), необходимо определить величину хотя бы одной из неизвестных реакций.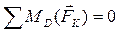
 (3.5)
(3.5)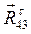 по модулю равна:
по модулю равна: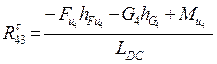

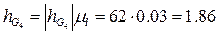 м
м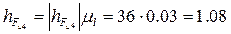 м
м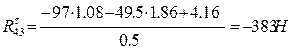
 и
и  найдем графически. Для этого построим план сил по уравнению (3.4).
найдем графически. Для этого построим план сил по уравнению (3.4).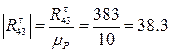 мм
мм мм
мм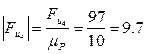 мм
мм мм
мм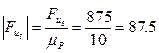 мм
мм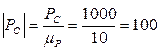 мм
мм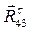 , который в масштабном выражении равен 38,3 мм. Из конца вектора
, который в масштабном выражении равен 38,3 мм. Из конца вектора 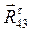 отложим вектор
отложим вектор 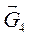 , который в масштабном выражении равен 5 мм и т. д., согласно уравнению (3.5). Последний вектор, который мы можем отложить, вектор
, который в масштабном выражении равен 5 мм и т. д., согласно уравнению (3.5). Последний вектор, который мы можем отложить, вектор 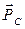 , он также известен по направлению и величине (рис. 3.6).
, он также известен по направлению и величине (рис. 3.6).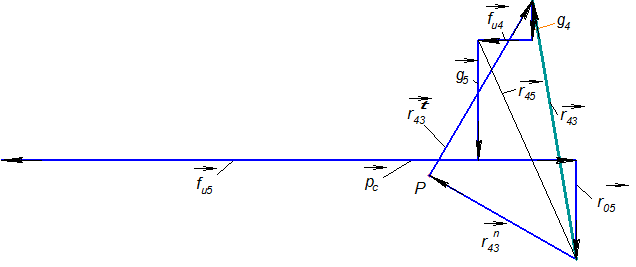
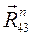 , его направление перпендикулярно
, его направление перпендикулярно  ), а из конца построений (вектора
), а из конца построений (вектора 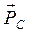 ) – направление другого неизвестного по величине вектора (
) – направление другого неизвестного по величине вектора (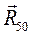 , его направление - горизонтальная линия). Полученная точка пересечения и определит длины отрезков, которые в масштабе
, его направление - горизонтальная линия). Полученная точка пересечения и определит длины отрезков, которые в масштабе 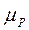 изображают неизвестные векторы. Сложив геометрически векторы
изображают неизвестные векторы. Сложив геометрически векторы 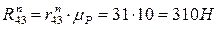
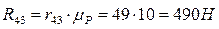

 между звеньями 4 и 5 в группе составим векторное уравнение равновесия всех сил для 4 -го звена:
между звеньями 4 и 5 в группе составим векторное уравнение равновесия всех сил для 4 -го звена: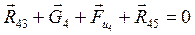 (3.6)
(3.6)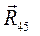 . Мы можем построить план сил по уравнению (3.6), а можем на уже построенном плане сил для структурной группы (рис. 3.6) соединить конец вектора
. Мы можем построить план сил по уравнению (3.6), а можем на уже построенном плане сил для структурной группы (рис. 3.6) соединить конец вектора  с началом вектора
с началом вектора  и получить искомый вектор
и получить искомый вектор 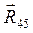 .
.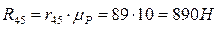
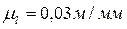 . К звеньям 2-3 будут приложены следующие силы:
. К звеньям 2-3 будут приложены следующие силы: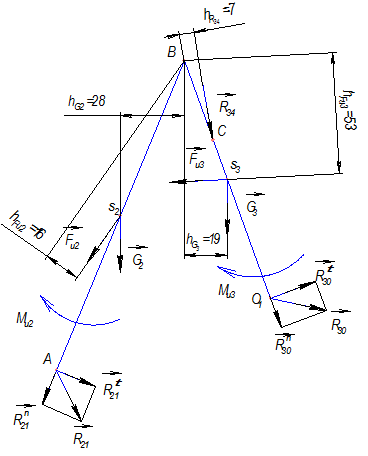
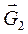 и
и 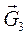 , приложенные в центрах тяжести.
, приложенные в центрах тяжести.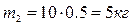

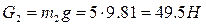
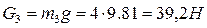
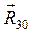 для вращательной пары 3-0, которую разложим на две составляющие: нормальную
для вращательной пары 3-0, которую разложим на две составляющие: нормальную 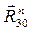 и тангенциальную
и тангенциальную 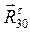 ;
; 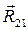 для вращательной пары 2-1, которую также разложим на две составляющие: нормальную
для вращательной пары 2-1, которую также разложим на две составляющие: нормальную  и тангенциальную
и тангенциальную  ;
;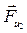 , направленная противоположно ускорению
, направленная противоположно ускорению  ,
,  , направленная противоположно ускорению
, направленная противоположно ускорению  (см. план ускорений) и моменты
(см. план ускорений) и моменты  и
и 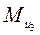 , направленные противоположно угловым ускорениям соответственно
, направленные противоположно угловым ускорениям соответственно  и
и  . При этом
. При этом Н
Н Н
Н Нм
Нм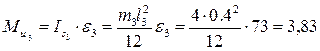 Нм
Нм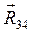 , модуль которой, согласно третьему закону Ньютона, равен реакции
, модуль которой, согласно третьему закону Ньютона, равен реакции  (см. предыдущий план сил), т. е.
(см. предыдущий план сил), т. е.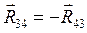 (3.7)
(3.7) и
и 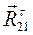 .
.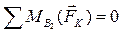
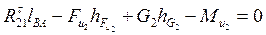 (3.8)
(3.8)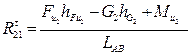
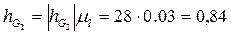 м
м м
м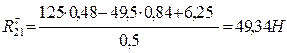

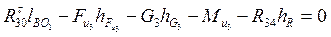 (3.9)
(3.9)
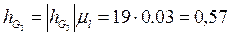 м
м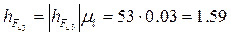 м
м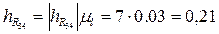 м
м
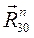 и
и 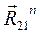 найдем графически. Для этого составляем векторное уравнение равновесия всех сил для структурной группы:
найдем графически. Для этого составляем векторное уравнение равновесия всех сил для структурной группы: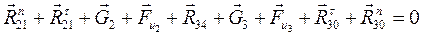 (3.10)
(3.10)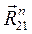 и
и 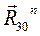 . Найдем их, построив план сил по уравнению (3.10).
. Найдем их, построив план сил по уравнению (3.10).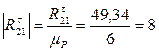 мм
мм мм
мм мм
мм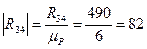 мм
мм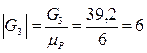 мм
мм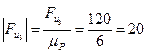 мм
мм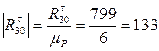 мм
мм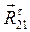 , который в масштабном выражении равен 8 мм. Из конца вектора
, который в масштабном выражении равен 8 мм. Из конца вектора 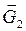 , который в масштабном выражении равен 8 мм и т. д., согласно уравнению (3.10). Последний вектор, который мы можем отложить, вектор
, который в масштабном выражении равен 8 мм и т. д., согласно уравнению (3.10). Последний вектор, который мы можем отложить, вектор 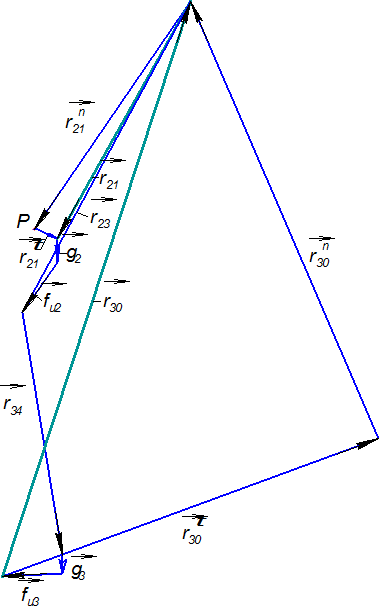
 , его направление перпендикулярно
, его направление перпендикулярно 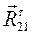 ), а из конца построений (вектора
), а из конца построений (вектора 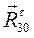 ) – направление другого неизвестного по величине вектора (
) – направление другого неизвестного по величине вектора ( изображают неизвестные векторы. Сложив геометрически векторы
изображают неизвестные векторы. Сложив геометрически векторы 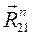 и
и 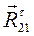 , получим суммарную реакцию в кинематической паре
, получим суммарную реакцию в кинематической паре  . Сложив геометрически векторы
. Сложив геометрически векторы 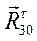 , получим суммарную реакцию в кинематической паре
, получим суммарную реакцию в кинематической паре 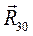 .
.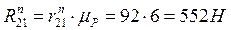
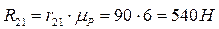


 в группе составим векторное уравнение равновесия всех сил для 2-го звена:
в группе составим векторное уравнение равновесия всех сил для 2-го звена: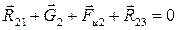 (3.11)
(3.11) . На построенном плане сил для структурной группы (рис. 3.8) соединяем конец вектора
. На построенном плане сил для структурной группы (рис. 3.8) соединяем конец вектора  с началом вектора
с началом вектора 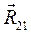 и получаем искомый вектор
и получаем искомый вектор 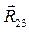 .
.
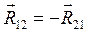
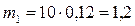 кг.
кг.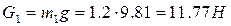 .
.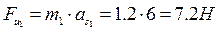 .
.
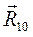 в любом направлении, не раскладывая.
в любом направлении, не раскладывая. , называемой уравновешивающей. Обычно она прикладывается в точке А перпендикулярно кривошипу ОА. Значение этой силы определяется из уравнения моментов сил относительно точки О:
, называемой уравновешивающей. Обычно она прикладывается в точке А перпендикулярно кривошипу ОА. Значение этой силы определяется из уравнения моментов сил относительно точки О:
 (3.12)
(3.12)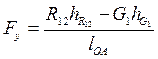
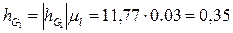 м
м м
м
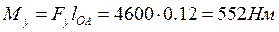 .
. и
и  (движущего момента) противоположны.
(движущего момента) противоположны.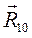 в кинематической паре 1-0 определяется путем построения плана сил по уравнению:
в кинематической паре 1-0 определяется путем построения плана сил по уравнению: (3.13)
(3.13)
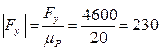 мм
мм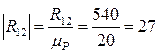 мм
мм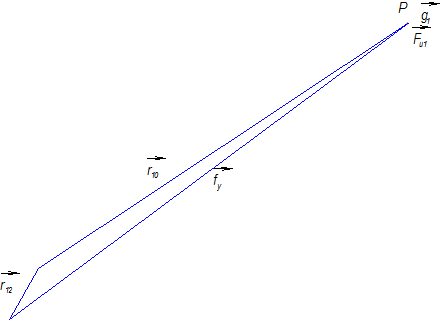
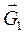 и
и 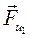 в масштабном выражении равны нулю, поэтому откладываем вектор
в масштабном выражении равны нулю, поэтому откладываем вектор 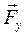 , который в масштабном выражении равен 230 мм. Из его конца отложим вектор
, который в масштабном выражении равен 230 мм. Из его конца отложим вектор 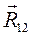 , который в масштабном выражении равен 27 мм. Соединив конец
, который в масштабном выражении равен 27 мм. Соединив конец  с полюсом Р, получим вектор
с полюсом Р, получим вектор 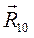 .
.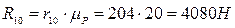
 , приложенная в заданной точке механизма. Такой метод называется методом рычага Жуковского.
, приложенная в заданной точке механизма. Такой метод называется методом рычага Жуковского. которой равна (рис. 3.11)
которой равна (рис. 3.11)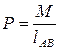 (3.14)
(3.14)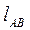 - расстояние в м между точками А и В приложения сил Р, образующих пару с моментом М.
- расстояние в м между точками А и В приложения сил Р, образующих пару с моментом М.
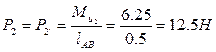

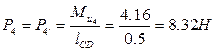
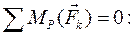
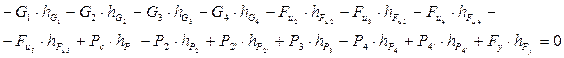 (3.15)
(3.15)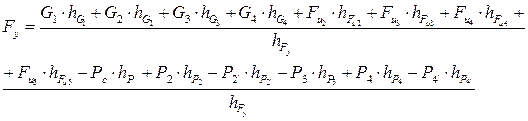
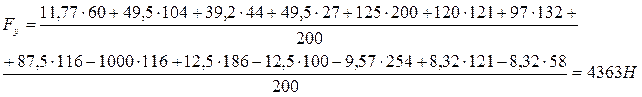 Относительная разность между значениями уравновешивающих сил, определенными разными методами
Относительная разность между значениями уравновешивающих сил, определенными разными методами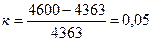 .
.
 .
.
 ;
;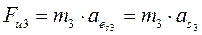 (величину и направление вектора ускорения центра тяжести звена 3 -
(величину и направление вектора ускорения центра тяжести звена 3 -  смотрим на плане ускорений);
смотрим на плане ускорений); ;
;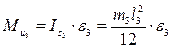 ;
; 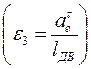 ;
;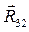 в кинематической паре из звеньев 2 и 3 (направленную перпендикулярно движению камня 2 в любую сторону, величина её неизвестна);
в кинематической паре из звеньев 2 и 3 (направленную перпендикулярно движению камня 2 в любую сторону, величина её неизвестна); в кинематической паре из звеньев 3 и 0 (направленную в любую сторону).
в кинематической паре из звеньев 3 и 0 (направленную в любую сторону).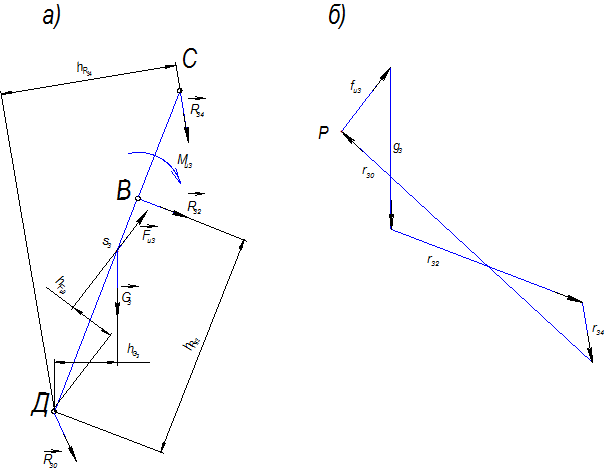
 (3.16)
(3.16) .
. (3.17)
(3.17)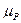 и вычисляем отрезки, которые будут отображать векторы уравнения (3.17) на плане сил.
и вычисляем отрезки, которые будут отображать векторы уравнения (3.17) на плане сил. .
.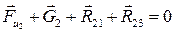 (3.18)
(3.18) .
. (
( - вектор абсолютного ускорения точки В).
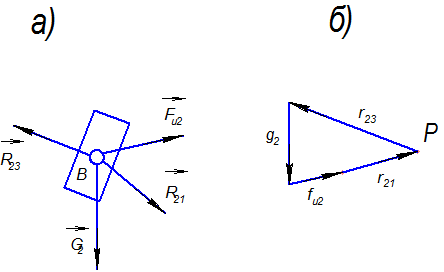
- вектор абсолютного ускорения точки В). .
.
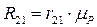 .
.


