
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Соединения призматическими шпонкамиСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте Прочность соединений призматическими и сегментными шпонками рассчитывают по напряжениям смятия s см и среза t с (рис. 9.6). Рис. 9.6. К расчёту призматических и сегментных шпонок Напряжения смятия s см возникают по длине шпонки l на высоте k. Для призматических шпонок со скруглёнными концами вместо длины l в расчётные формулы напряжений подставляют рабочую длину шпонки l p:
где b – ширина шпонки, мм. Расчётные напряжения смятия s см определяются по формуле
где T – передаваемый шпонкой крутящий момент, Н×мм; Величина k определяется как разность размеров шпонки При стальной ступице и спокойной нагрузке допускаемые напряжения смятия [ s см] £ 100 МПа (Н/мм2); при колебаниях нагрузки их следует снижать на 20÷25 %; при ударной нагрузке – снижать на 40÷50 %; при насаживаемых на вал чугунных деталях приведённые значения [ s см] снижать вдвое. Напряжения среза t с возникают по ширине шпонки b на рабочей длине l p и рассчитываются по следующей формуле:
где b – ширина шпонки, мм. Допускаемые напряжения на срез [ t c] = 0,6 [ s см]. Соединения клиновыми шпонками Соединения клиновыми шпонками рассчитывают по напряжениям смятия s см (рис. 9.7). Рис. 9.7. К расчёту прочности клиновых врезных шпонок Напряжения смятия sсм распределяются по ширине шпонки b по закону треугольника и могут быть рассчитаны по формуле
где T – передаваемый крутящий момент, Н×мм; l – длина шпонки, мм; b – ширина шпонки, мм; d – диаметр вала, мм; f – коэффициент трения между шпонкой и ступицей, f = 0,15÷0,2. Допускаемое напряжение смятия [ s см] = 100÷150 МПа. Если расчёт на прочность не сходится (расчётные напряжения смятия и среза превышают допускаемые более, чем на 5 %), то устанавливают две шпонки. Призматические шпонки устанавливаются под углом 180°, клиновые – под углом 120°, сегментные – в один ряд по длине ступицы. Однако часто вместо многошпоночных используют шлицевые соединения. Шлицевые (зубчатые) соединения Общая характеристика Шлицевые соединения используют для соединения вала со ступицей. Шлицы – это выступы на валу, которые входят в соответствующие пазы ступицы. К достоинствам шлицевых соединений относятся: детали лучше центрируются на валах и имеют лучшее направление при осевом перемещении; прочность соединения, особенно при динамических нагрузках, повышается за счёт увеличения суммарной длины рабочих поверхностей зубьев по сравнению со шпоночными соединениями; равномерное распределение нагрузки по окружности вала. К недостатку шлицевого соединения относится – много переходов сечений (острых углов), вызывающих концентрацию напряжений, что снижает прочность шлицев. Шлицевые соединения применяются в тяжелонагруженных машинах (автотракторные агрегаты, станкостроение, авиастроение и т. д.). Конструкции шлицевых соединений делятся по форме профиля зуба (шлица). В соответствии с этим и в зависимости от способа центрирования различают следующие виды шлицевых соединений: прямобочные (рис. 9.8); эвольвентные (рис. 9.9); треугольные (рис. 9.10). Для прямобочных шлицев центрирование по ширине шлица b обеспечивает более равномерное распределение нагрузки между шлицами, но не даёт точной соосности ступицы и вала. Применяется при передаче больших крутящих моментов, где не требуется точности центрирования (например, агрегаты автомобиля). Центрирование по наружному D и внутреннему d диаметрам обеспечивает точное центрирование ступицы и вала. Применяется в ответственных соединениях, где требуется точное совпадение геометрических осей соединяемых деталей. а) б) в)
Рис. 9.8. Шлицы с прямобочным профилем: а – с центрированием по ширине шлица b; б – с центрированием по наружному диаметру D; в – с центрированием по внутреннему диаметру d
Эвольвентные шлицы изготавливают с центрированием по боковым сторонам S и наружному диаметру D. По сравнению с прямобочными более прочны, просты и дешевы в изготовлении. Треугольные шлицы применяют в качестве неподвижного соединения при передаче небольших моментов. Центрирование только по боковым сторонам S. Применяются так же как конические с конусностью 1:16. Расчёт и конструирование Длина шлицев равна длине ступицы. Размеры шлицев (ширина и фаска) и их число z определяются по соответствующему стандарту в зависимости от диаметра вала d, где они расположены. Стандартом предусмотрены три серии шлицев с прямобочными зубьями: лёгкая, средняя и тяжёлая в зависимости от режима их работы. После определения размеров и длины шлицев производится проверочный расчёт их прочности по напряжениям смятия sсм (рис. 9.11). Расчётные напряжения смятия s см для прямобочных шлицев рассчитываются по формуле:
где T – передаваемый крутящий момент, Н×мм; l – длина шлицев, мм; h – рабочая высота шлица, мм; h = 0,5 (D – d) – f; f – фаска, мм; d c – средний диаметр шлица, мм; d c = 0,5(D+d) – для прямобочных; z – число шлицев; y – коэффициент неравномерности распределения нагрузки между шлицами, y = 0,7÷0,8. Рис. 9.11. К расчёту прочности шлицевого соединения Шлицевые соединения с эвольвентными шлицами (рис. 9.12) более прочны и технологичны в изготовлении по сравнению с прямобочными. Для эвольвентных шлицев напряжения s см определяют по формуле
где D – наружный (номинальный) диаметр, мм; m – модуль, мм. Допускаемые напряжения для шлицевых соединений определяются в зависимости от режима работы, вида соединения и термообработки.
Рис. 9.12. Расчётная схема эвольвентного шлицевого соединения Резьбовые соединения Общие сведения Резьбовые соединения деталей машин относятся к разъёмным соединениям. Они получили наибольшее распространение вследствие своей универсальности, простоты изготовления, надёжности, удобства сборки и разборки, полной взаимозаменяемости. Основными деталями резьбовых соединений являются болты, винты, гайки и шпильки (рис. 9.13). а) б) в) Рис. 9.13. Конструктивные разновидности резьбовых соединений: а – болтом; б – винтом; в – шпилькой Болтами соединяют детали относительно небольшой толщины и применяют для материалов, не обеспечивающих требуемую надёжность резьбы. Винты применяют: когда одна из скрепляемых деталей имеет относительно большую толщину, при отсутствии места под гайки, при жёстком требовании к уменьшению массы изделия, а также для придания изделию красивого внешнего вида. Шпильки применяют вместо винтов в случаях, когда материал скрепляемой детали с резьбовым отверстием не обеспечивает требуемой долговечности при повторяющихся сборке и разборке. Основным элементом резьбового соединения является резьба. Профиль резьбы – это контур сечения резьбы в плоскости, проходящей через ось основной поверхности. Профиль резьбы определяется формой сечения витков в осевой плоскости. По форме основной поверхности различают цилиндрические и конические резьбы. Наиболее распространена цилиндрическая резьба. Коническую резьбу применяют для плотных соединений труб, маслёнок, пробок и т. п. По форме профиля различают треугольные, прямоугольные, трапецеидальные и круглые резьбы (рис. 9.14). По направлению винтовой линии различают правую и левую резьбы. У правой резьбы винтовая линия идет слева направо и вверх, у левой – справа налево и вверх. Наиболее распространена правая резьба. Левую резьбу применяют только в специальных случаях. По числу заходов различают однозаходную, двухзаходную и четырёхзаходную резьбы. Все крепёжные резьбы однозаходные. Многозаходные резьбы применяются преимущественно в винтовых механизмах. Геометрические параметры резьбы: наружный диаметр d (номинальный), внутренний диаметр d 1 (используется в прочностных расчётах), средний диаметр d 2 (диаметр воображаемого цилиндра, образующая которого пересекает резьбу в таком месте, где ширина выступа равна ширине впадины (используется для геометрических расчётов)), рабочая высота профиля h, по которой соприкасаются боковые стороны резьбы болта и гайки, шаг p, ход, угол профиля a. Все геометрические параметры резьбы и допуски на них стандартизованы.
а) б) в) г) д) е) Рис. 9.14. Основные типы резьбы: а – треугольная; б – трубная; в – трапецеидальная; г – упорная; Основные типы резьбы. По назначению различают резьбы крепёжные (метрическая с треугольным профилем, трубная, круглая) и резьбы для винтовых механизмов или ходовые (прямоугольная, трапецеидальная симметричная, трапецеидальная несимметричная упорная). 9.4.2 Расчёт резьбовых соединений Выход из строя болтов и винтов происходит из-за разрыва их стержня по резьбе или по переходному сечению у головки, либо в результате разрушения резьбы, либо из-за разрушения головки. Шпильки выбывают из строя вследствие разрыва их стержня по резьбе, повреждения или разрушения резьбы. Размеры стандартных резьбовых деталей отвечают условию равнопрочности по основному критерию работоспособности – прочности нарезанной части (резьбы) их стержня. Из расчёта стержня на прочность определяют номинальный диаметр резьбы, как правило, – внутренний d 1. Длину резьбовых деталей принимают в зависимости от толщины соединяемых деталей. Остальные размеры принимают в зависимости от диаметра резьбы по соответствующим стандартам. Рассмотрим основные случаи расчёта одиночной резьбовой детали при статическом нагружении (три первых – осевая растягивающая сила; два последних – поперечная сила). Первый случай. Болт нагружен осевой растягивающей силой; предварительная и последующая затяжка его отсутствуют (соединение ненапряжённое) (рис. 9.15).
К болтам этой категории обычно относятся те из них, которые находятся под действием сил тяжести (например, резьбовой конец грузового крюка грузоподъёмной машины). Условие прочности проверочного расчёта болта в этом случае имеет вид:
где Напряжение
где Проектировочный расчёт для этого случая нагружения выполняется по формуле
Второй случай. Болт испытывает растяжение и кручение, обусловленное его затяжкой. Болт, одновременно работающий на растяжение и кручение, рассчитывают только на растяжение (случай 1) по допускаемому напряжению на растяжение, уменьшенному в 1,3 раза или по расчётной силе, увеличенной в 1,3 раза по сравнению с силой, растягивающей болт. Проектный расчёт болта в этом случае производится по формуле
Это решение применимо для болтов, нагруженных растягивающими силами и испытывающих кручение от подтягивания гаек под нагрузкой, например в винтовых стяжках. Третий случай. Предварительно затянутый болт дополнительно нагружен внешней осевой растягивающей силой (рис. 9.16). Этот случай – самый распространённый, обеспечивающий плотность соединения и отсутствие смещений деталей стыка (болты фланцев, крышек, фундаментов и т. п.) После предварительной затяжки болта он растягивается, а детали стыка сжимаются.
При действии на соединение внешней силы F только часть её cF дополнительно нагружает болт, а остальная часть Коэффициент c, учитывающий долю внешней нагрузки на болт, – коэффициент внешней (основной) нагрузки. При отсутствии упругих прокладок c = 0,2…0,3; при наличии – c = 0,5. Условие нераскрытия стыка определяется формулой
где При постоянной внешней нагрузке, без упругих прокладок в стыке коэффициент k = 1,25…2; при переменной – k = 2…4. Таким образом, осевая растягивающая болт сила
Проектный расчёт с учётом последующей затяжки в этом случае:
Четвёртый случай. Болт, установленный в отверстие с зазором, нагружен поперечной силой (рис. 9.17). В этом случае болт затягивается такой силой затяжки F з, чтобы сила трения F Т в стыке соединяемых деталей уравновешивала бы внешнюю силу F, т. е.:
где f – коэффициент трения между соединяемыми деталями, который для стальных и чугунных деталей принимается в диапазоне f = 0,15…0,2. Проектный расчёт болта в этом случае производится с учётом 20 % запаса от сдвига деталей и с учётом крутящего момента при затяжке болта по формуле:
Пятый случай. Болт, установленный в отверстие из-под развёртки без зазора (призонный), нагружен поперечной силой F (рис. 9.18). В этом случае болт рассчитывают на срез; проверочное условие прочности болта:
где t с – расчётное напряжение среза болта, МПа; F – поперечная внешняя сила, срезающая болт, Н; d – диаметр стержня болта в опасном сечении, мм; [ t с] – допускаемое напряжение на срез болта.
[ t с] определяется как 0,4 σ Т для статических нагрузок. Проектировочный расчёт болта выполняется по формуле
Справочные данные для расчёта приведены в [4]. Механические передачи
|
||||||||||||
|
Последнее изменение этой страницы: 2016-04-07; просмотров: 637; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.141 (0.012 с.) |

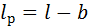 , (9.8)
, (9.8)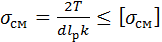 , (9.9)
, (9.9) .
. , (9.10)
, (9.10)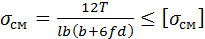 , (9.11)
, (9.11)
 Рис. 9.9. Шлицы с эвольвентным профилем:
а – с центрированием по ширине шлица S; б – с центрированием по наружному диаметру D
Рис. 9.9. Шлицы с эвольвентным профилем:
а – с центрированием по ширине шлица S; б – с центрированием по наружному диаметру D
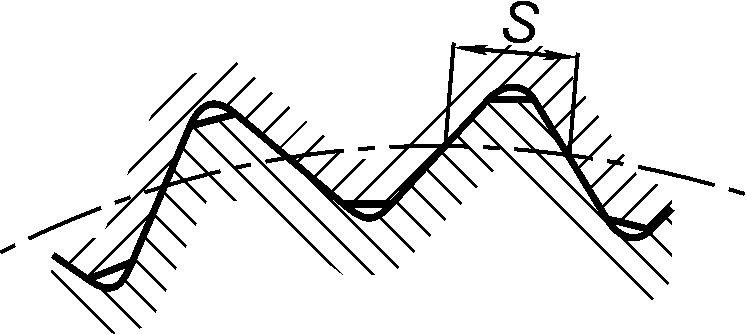 Рис. 9.10. Шлицы с треугольным профилем
Рис. 9.10. Шлицы с треугольным профилем
 , (9.12)
, (9.12) , (9.13)
, (9.13) , (9.14)
, (9.14) – расчётное напряжение растяжения в поперечном сечении нарезанной части болта, МПа; F – сила, растягивающая болт, Н;
– расчётное напряжение растяжения в поперечном сечении нарезанной части болта, МПа; F – сила, растягивающая болт, Н;  – допускаемое напряжение на растяжение для болта, МПа.
– допускаемое напряжение на растяжение для болта, МПа. рассчитывают по формуле:
рассчитывают по формуле: , (9.15)
, (9.15) – предел текучести материала болта, МПа; [ S ] – допускаемый коэффициент запаса прочности для болтов из углеродистых сталей, при статической нагрузке принимают [ S ] = 1,3…2,5.
– предел текучести материала болта, МПа; [ S ] – допускаемый коэффициент запаса прочности для болтов из углеродистых сталей, при статической нагрузке принимают [ S ] = 1,3…2,5. . (9.16)
. (9.16) . (9.17)
. (9.17) разгружает детали стыка от сжатия.
разгружает детали стыка от сжатия. , (9.18)
, (9.18) – усилие затяжки болта; k – коэффициент затяжки болта.
– усилие затяжки болта; k – коэффициент затяжки болта. , действующая на него после предварительной затяжки и приложения к соединению внешней силы F, будет равна:
, действующая на него после предварительной затяжки и приложения к соединению внешней силы F, будет равна: . (9.19)
. (9.19) . (9.20)
. (9.20) , (9.21)
, (9.21) . (9.22)
. (9.22) , (9.23)
, (9.23) . (9.24)
. (9.24)


