
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Скорость по диаграмме Ф. ВиттенбауэраСодержание книги
Поиск на нашем сайте
 от приведённого момента инерции от приведённого момента инерции  . Диаграмма строится по графикам . Диаграмма строится по графикам  и и  . Для этого при каждом . Для этого при каждом 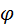 замеряют замеряют  , ,  и откладывают замеренное по одноимённым осям диаграммы (рис. 7.3). и откладывают замеренное по одноимённым осям диаграммы (рис. 7.3).
Каждую точку диаграммы нумеруют соответственно разбивке оси Пусть
Как показывает формула, скорость изменяется соответственно углу Дифференциальное уравнение движения машины Пусть механизм машины имеет одну степень свободы и звено приведения совершает вращательное движение. Тогда динамическая модель машины будет иметь вид, показанный на рис. 7.4. Согласно известной теореме, приращение кинетической энергии машины равно приращению работы внешних сил: Приращение работы
Отношение
После подстановки
Это и есть дифференциальное уравнение движения машины. Оно проще, чем уравнения Лагранжа второго рода, но применимо к механизмам только с одной степенью свободы. Интегрированием дифференциального уравнения находят закон движения машины. Подбор маховика Как уже отмечалось, при установившемся движении диаграмма Виттенбауэра имеет вид замкнутой кривой (рис. 7.5). Переходя от одной точки диаграммы к другой и следя за углом радиус-вектора, находят, что звено приведения вращается неравномерно, его скорость периодически меняется, колеблясь около некоторого среднего значения Индекс
Верхние индексы – для
где среднюю скорость
Пусть у исследуемой машины неравномерность вращения звена приведения оказалась больше, чем требуется, т. е.
Затем из (7.4) выводят и вычисляют требуемые углы касательных
Проводя касательные под требуемыми углами, находят, что начало координат должно переместиться из точки 0 в точку 0¢. При этом приведённый момент инерции и кинетическая энергия машины должны возрасти на некоторую величину. Увеличение момента инерции обеспечивают путём установки на вал звена приведения массивного диска, называемого маховиком. Момент инерции маховика
На рис. 7.7 показан кривошипный механизм с маховиком 1, установленным на валу кривошипа. Кривая 2 показывает скорость кривошипа до установки маховика, кривая 3 – после. Как видим, после установки размах колебаний скорости становится меньше. Рис. 7.7. Влияние маховика на неравномерность вращения кривошипа
|
|||||||||
|
Последнее изменение этой страницы: 2016-04-07; просмотров: 717; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.217.4.250 (0.009 с.) |

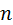 соответствуют началу и концу всего периода работы машины. Режиму установившегося движения соответствует замкнутый участок диаграммы. Текущая точка диаграммы пробегает по этому участку столько раз, сколько циклов содержит установившееся движение. Глядя на диаграмму, не следует думать, что кинетическая энергия зависит от приведённого момента инерции физически. Диаграмма всего лишь объединяет два графика в один.
соответствуют началу и концу всего периода работы машины. Режиму установившегося движения соответствует замкнутый участок диаграммы. Текущая точка диаграммы пробегает по этому участку столько раз, сколько циклов содержит установившееся движение. Глядя на диаграмму, не следует думать, что кинетическая энергия зависит от приведённого момента инерции физически. Диаграмма всего лишь объединяет два графика в один. ,
,  есть масштабные коэффициенты по осям диаграммы Виттенбауэра,
есть масштабные коэффициенты по осям диаграммы Виттенбауэра, 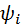 – угол радиус-вектора
– угол радиус-вектора  текущей точки диаграммы. Тогда согласно формуле (5.1), в точке
текущей точки диаграммы. Тогда согласно формуле (5.1), в точке  скорость звена приведения
скорость звена приведения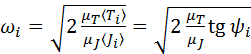 . (7.2)
. (7.2) , то и
, то и  ; если
; если  растёт, то и
растёт, то и  растёт. Следя за углом, можно предсказать поведение скорости, не производя вычислений. В этом состоит достоинство диаграммы Виттенбауэра.
растёт. Следя за углом, можно предсказать поведение скорости, не производя вычислений. В этом состоит достоинство диаграммы Виттенбауэра. .
. . С учётом этого,
. С учётом этого,  . Отсюда:
. Отсюда:  .
.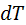 к
к  можно рассматривать как производную от кинетической энергии по углу поворота звена приведения. Кинетическая энергия
можно рассматривать как производную от кинетической энергии по углу поворота звена приведения. Кинетическая энергия 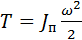 . Дифференцируя по
. Дифференцируя по  . Произведение
. Произведение  приводимо к более простому и понятному виду:
приводимо к более простому и понятному виду: .
.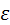 в исходное выражение формула приведённого момента принимает вид:
в исходное выражение формула приведённого момента принимает вид: . (7.3)
. (7.3) (рис. 7.6).
(рис. 7.6).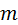 происходит от английского
происходит от английского 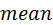 и означает – среднее. Экстремальным скоростям
и означает – среднее. Экстремальным скоростям  ,
, 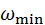 соответствуют экстремальные углы
соответствуют экстремальные углы 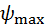 ,
,  радиус-вектора. При экстремальных углах радиус-вектор становится касательным к диаграмме Виттенбауэра. Проводя касательные и замеряя углы их наклона, находят экстремальные скорости
радиус-вектора. При экстремальных углах радиус-вектор становится касательным к диаграмме Виттенбауэра. Проводя касательные и замеряя углы их наклона, находят экстремальные скорости  . (7.4)
. (7.4)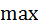 , нижние – для
, нижние – для  . Степень неравномерности вращения звена приведения оценивают коэффициентом неравномерности
. Степень неравномерности вращения звена приведения оценивают коэффициентом неравномерности , (7.5)
, (7.5) . (7.6)
. (7.6) , где
, где  – требуемый коэффициент неравномерности. Тогда из формул (7.5), (7.6) выводят требуемые экстремумы скорости
– требуемый коэффициент неравномерности. Тогда из формул (7.5), (7.6) выводят требуемые экстремумы скорости .
. .
. .
.


