
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Среднее передаточное отношениеСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Анализируемый механизм преобразует вращательное движение со скоростью
Согласно формуле, скорости колёс обратно пропорциональны числам их зубьев. При выводе формулы молчаливо предполагалось, что скорости колёс постоянны. Это возможно лишь при специально подобранных профилях зубьев. При случайных профилях и постоянной скорости одного из колёс скорость другого будет, скорее всего, переменной. Точно так же будет вести себя и передаточное отношение, в частности, Мгновенное передаточное отношение Переставим механизм на колесо 1 (рис. 5.1, б) и найдём мгновенный центр вращения колеса 2. Мгновенный центр должен находиться на пересечении перпендикуляров к скоростям каких-нибудь двух точек колеса 2. Очевидно направление скорости
Рис. 5.1. Определение мгновенного передаточного отношения Как бы ни двигалась точка По свойству мгновенного центра скоростей Выражая скорости точек
В отличие от среднего, это точное передаточное отношение. Оно называется мгновенным, относящимся только к данной фазе зацепления. Профили зубьев должны быть подобраны так, чтобы мгновенное передаточное отношение в любой фазе зацепления было равно среднему, определяемому числами зубьев. В плоском зацеплении мгновенный центр вращения и мгновенный центр скоростей одного колеса относительно другого называется полюсом зацепления. Если говорить об абсолютных движениях, т. е. о движениях относительно стойки, то полюс зацепления – это точка, в которой скорости зубчатых колёс равны друг другу: Из решения задачи о мгновенном передаточном отношении вытекает основная теорема плоского зацепления: «Нормаль к профилям зубьев, проведённая через точку их касания, пересекает линию центров в полюсе зацепления и делит эту линию на части, обратно пропорциональные скоростям колёс». Центроиды зацепления Центроиды состоят из точек Центроиды обладают двумя важными свойствами: они всегда касаются друг друга и перекатываются друг по другу без скольжения. Первое свойство вытекает из образования центроид проколами сразу двух плоскостей, второе следует из равенства скоростей в точке касания. Радиусы круглых центроид выводят из системы
Первое уравнение системы вытекает из свойства центроид всегда касаться друг друга, второе получается из уравнений (5.1), (5.2). Первое научно обоснованное зацепление, обладающее постоянным передаточным отношением в любой фазе зацепления, было циклоидальным с профилями зубьев, очерченными по циклоидам. Циклоидой называется кривая, описываемая точкой окружности при перекатывании её по другой окружности или прямой. Своё первое применение циклоидальное зацепление нашло в часовых механизмах и сохранилось там до сих пор. В других механизмах циклоидальное зацепление было вытеснено эвольвентным, предложенным математиком, швейцарцем по происхождению, Леонардом Эйлером в 1750 году. Это примерно на сто лет позже изобретения циклоидального зацепления. Эвольвентное зацепление 5.2.1 Принцип образования зацепления По произвольным окружностям, вращающимся вокруг своих центров
 . След точки на плоскости каждого из колёс образует кривые Э 1, Э 2, которые называются эвольвентами, по ним и очерчивают профили зубьев. Участки профилей, расположенные внутри окружностей обката, нарисованы пока произвольно. Эвольвентное зацепление можно представить также как след точки, которая принадлежит нити, перематывающейся с одной окружности на другую. . След точки на плоскости каждого из колёс образует кривые Э 1, Э 2, которые называются эвольвентами, по ним и очерчивают профили зубьев. Участки профилей, расположенные внутри окружностей обката, нарисованы пока произвольно. Эвольвентное зацепление можно представить также как след точки, которая принадлежит нити, перематывающейся с одной окружности на другую.
Рисующая точка оказывается одновременно и точкой касания нарисованных кривых. Траектория Физически передаточное отношение задают окружности, по которым катится прямая
Радиусы
|
|||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-07; просмотров: 490; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.14.247.170 (0.006 с.) |

 во вращательное со скоростью
во вращательное со скоростью  . Пусть число зубьев
. Пусть число зубьев 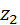 колеса 2 в два раза больше числа зубьев
колеса 2 в два раза больше числа зубьев 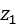 колеса 1. Тогда за один оборот большего колеса меньшее сделает два оборота. Во столько же будут отличаться и скорости колёс. Распространяя этот вывод на произвольное число зубьев, получают:
колеса 1. Тогда за один оборот большего колеса меньшее сделает два оборота. Во столько же будут отличаться и скорости колёс. Распространяя этот вывод на произвольное число зубьев, получают: . (5.1)
. (5.1)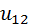 будет колебаться около значения
будет колебаться около значения  . Следовательно, формула (5.1) выражает лишь среднее передаточное отношение.
. Следовательно, формула (5.1) выражает лишь среднее передаточное отношение.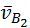 точки
точки  , оно перпендикулярно АВ. Не столь очевидно, но всё же определимо направление скорости
, оно перпендикулярно АВ. Не столь очевидно, но всё же определимо направление скорости  точки
точки  .
.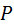 перпендикуляров к скоростям
перпендикуляров к скоростям  . Заметим попутно, что точка
. Заметим попутно, что точка  , совпадающая с
, совпадающая с  , т. е. скорость точки
, т. е. скорость точки  (см. рис. 5.1, а).
(см. рис. 5.1, а). . Отсюда передаточное отношение
. Отсюда передаточное отношение . (5.2)
. (5.2) (5.3)
(5.3)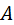 и
и  , катится без скольжения прямая
, катится без скольжения прямая 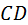 (рис. 5.2).
(рис. 5.2). точки касания зубьев называется линией зацепления. При эвольвентных профилях (и только эвольвентных) траектория точки касания или, иначе, линия зацепления прямая. Эта прямая оказывается также контактной нормалью. Нормаль пересекает линию центров в полюсе
точки касания зубьев называется линией зацепления. При эвольвентных профилях (и только эвольвентных) траектория точки касания или, иначе, линия зацепления прямая. Эта прямая оказывается также контактной нормалью. Нормаль пересекает линию центров в полюсе 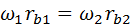 . Отсюда вытекает ещё одна формула передаточного отношения:
. Отсюда вытекает ещё одна формула передаточного отношения: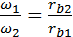 . (5.4)
. (5.4) ,
, 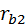 основных окружностей конкретного зацепления постоянны, поэтому передаточное отношение тоже постоянно, причём, не только в любой фазе зацепления, но и при любом межцентровом расстоянии. Независимостью передаточного отношения от колебаний межцентрового расстояния обладает только эвольвентное зацепление. Это свойство очень важно для практики, т. к. невозможно сделать что-либо абсолютно точно и сохранить эту точность в эксплуатации.
основных окружностей конкретного зацепления постоянны, поэтому передаточное отношение тоже постоянно, причём, не только в любой фазе зацепления, но и при любом межцентровом расстоянии. Независимостью передаточного отношения от колебаний межцентрового расстояния обладает только эвольвентное зацепление. Это свойство очень важно для практики, т. к. невозможно сделать что-либо абсолютно точно и сохранить эту точность в эксплуатации.


