
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Понятие передаточной функцииСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Целью рассмотрения САУ может быть решение одной из двух задач: задачи анализа или задачи синтеза. Но в любом случае порядок исследования систем включает в себя следующие этапы: математическое описание, исследование установившихся режимов, исследование переходных режимов. Рассмотрим случай, когда в замкнутой системе можно выделить объект управления ОУ и управляющее устройство УУ, как это показано на рис. 2.2.
Рис. 2.2 — Замкнутая САУ с единичной обратной связью
Общее уравнение САУ получается из системы уравнений объекта и управляющего устройства. Состояние объекта характеризуется выходной величиной
Состояние управляющего устройства характеризуется регулирующим воздействием
Приведенные уравнения полностью описывают процессы в САУ. Если в них исключить переменные
Уравнение (2.4) описывает поведение системы во времени, определяет переходные процессы и обычно называется уравнением динамики. Однако в форме дифференциальных уравнений математическое описание в теории автоматического управления обычно не применяется вследствие сложности решения таких уравнений. Исследование САУ существенно упрощается при использовании прикладных математических методов операционного исчисления. Возьмем некоторый элемент САУ, имеющий один вход и один выход. Если на его вход подать сигнал
Пусть
С учетом (2.6) дифференциальное уравнение (2.5), содержащее функции
Таким образом, формально переход от дифференциального уравнения к алгебраическому относительно изображения при нулевых начальных условиях получается путем замены символов дифференцирования оригиналов функций
Каждый элемент САУ в общем случае описывается дифференциальным уравнением вида (2.5). Следовательно, при выводе дифференциального уравнения системы в целом необходимо совместно решить систему дифференциальных уравнений. Преобразование Лапласа позволяет свести задачу решения системы дифференциальных уравнений высших порядков к решению системы алгебраических уравнений. Определив из алгебраических уравнений изображение Преобразование дифференциального уравнения по Лапласу дает возможность ввести одно из фундаментальных понятий — понятие передаточной функции. Из уравнения (2.7) определим отношение изображения выходной величины к изображению входной:
Отношение изображения выходной величины элемента (или системы) к изображению его входной величины при нулевых начальных условиях называется передаточной функцией элемента (или системы). Согласно (2.8) передаточная функция
где Из определения передаточной функции следует, что:
Передаточная функция является основной формой математического описания объектов в теории автоматического управления и так как она полностью определяет динамические свойства объекта, то первоначальная задача расчета САУ сводится к определению передаточной функции. Рассмотрим примеры по определению передаточных функций некоторых простейших схем, характерных для электроники. Пример 2.2
Процессы в схеме описываются уравнением
Перейдем к изображению по Лапласу:
Составим передаточную функцию как отношение изображения выходной величины к изображению входной величины:
где Передаточные функции принято записывать в такой форме, чтобы свободные члены полиномов от
Пример 2.3 Вывести передаточную функцию схемы на рис. 2.4, считая входной величиной напряжение
Система уравнений, описывающих процессы в устройстве, схема которого изображена на рис 2.4, имеет вид:
Подставив третье уравнение в первое, получим:
Перейдем к изображениям:
Передаточная функция
где
Пример 2.4 Вывести передаточную функцию схемы на рис. 2.5, считая входной величиной
Из второго и третьего уравнений соответственно получим:
Подставим полученные выражения
Передаточная функция:
где Пример 2.5 Вывести передаточную функцию схемы на рис. 2.6, считая входной величиной
Рис. 2.6 — Схема к примеру 2.5 Система уравнений электрического равновесия схемы для мгновенных значений величин:
Последнее соотношение здесь, конечно, не уравнение, а обозначение выходной величины. Уравнения в операторной форме:
Из второго уравнения
Подставим полученное значение
Последнее соотношение подставим в первое уравнение и определим передаточную функцию:
где
Пример 2.6 Вывести передаточную функцию схемы на рис. 2.7, а, содержащей операционный усилитель. Операционными усилителями называются усилители постоянного тока малой мощности, имеющие два входа — инвертирующий (–) и неинвертирующий (+). В настоящее время они выполняются по интегральной технологии, т.е. в виде микросхем, и характеризуются большими значениями коэффициента усиления ( Выведем вначале передаточную функцию для типового включения операционного усилителя, показанного на рис. 2.7, б, в общем виде.
Рис. 2.7 — К выводу передаточной функции устройства на операционном усилителе С учетом принятых допущений (
Следовательно, напряжение на инвертирующем входе приближенно равно нулю, отсюда
С учетом последней формулы можно легко получить выражение для передаточной функции устройства, схема которого приведена на рис. 2.7, б:
Знак минус в выражении (2.9) указывает на то, что полярность выходного напряжения схемы противоположна полярности входного напряжения.
Из курса электротехники известно, что операторные сопротивления конденсатора
Используя выражение для
Подставляя полученные соотношения в формулу (2.9), получим выражение передаточной функции схемы, взятое со знаком минус:
где
|
|||||||
|
Последнее изменение этой страницы: 2016-12-13; просмотров: 484; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.128.78.107 (0.012 с.) |


 , регулирующим воздействием
, регулирующим воздействием  и возмущением
и возмущением 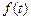 . Тогда выходная величина может быть представлена функцией:
. Тогда выходная величина может быть представлена функцией:
 . Процессы в УУ будут описываться двумя уравнениями:
. Процессы в УУ будут описываться двумя уравнениями:

 , то получим дифференциальное уравнение САУ:
, то получим дифференциальное уравнение САУ: (2.4)
(2.4)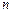 -й степени:
-й степени: (2.5)
(2.5) — изображения по Лапласу величин
— изображения по Лапласу величин  и
и  , в соответствии с теоремой о дифференцировании оригиналов [1, 2], получим
, в соответствии с теоремой о дифференцировании оригиналов [1, 2], получим . (2.6)
. (2.6)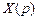 и
и 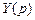 :
: (2.7)
(2.7) соответственно на
соответственно на 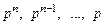 и функций
и функций  — их изображениями
— их изображениями  . С комплексной переменной
. С комплексной переменной 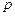 , как и с другими членами алгебраического уравнения, можно производить различные действия: умножение, деление, вынесение за скобки и т.д.
, как и с другими членами алгебраического уравнения, можно производить различные действия: умножение, деление, вынесение за скобки и т.д. . (2.8)
. (2.8)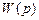 является дробно-рациональной функцией комплексной переменной
является дробно-рациональной функцией комплексной переменной 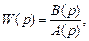
 — полином степени
— полином степени  — полином степени
— полином степени 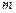 , причем
, причем  .
. .
. Вывести передаточную функцию для схемы на рис. 2.3, считая входным воздействием приложенное напряжение
Вывести передаточную функцию для схемы на рис. 2.3, считая входным воздействием приложенное напряжение  , а выходным — ток в цепи
, а выходным — ток в цепи  .
.

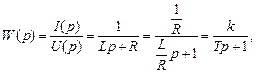
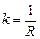 — коэффициент передачи,
— коэффициент передачи,  — постоянная времени.
— постоянная времени. , а выходной —
, а выходной —  .
. При выводе передаточной функции будем считать, что цепочка не нагружена (никаких элементов к выходным зажимам не подключено, либо эти элементы имеют сопротивление, стремящееся к бесконечности) и сопротивление источника входного напряжения настолько мало, что им можно пренебречь.
При выводе передаточной функции будем считать, что цепочка не нагружена (никаких элементов к выходным зажимам не подключено, либо эти элементы имеют сопротивление, стремящееся к бесконечности) и сопротивление источника входного напряжения настолько мало, что им можно пренебречь.


 ,
, — постоянная времени.
— постоянная времени. Составляем два уравнения по второму закону Кирхгофа, одно уравнение по первому закону Кирхгофа и расписываем выходную величину:
Составляем два уравнения по второму закону Кирхгофа, одно уравнение по первому закону Кирхгофа и расписываем выходную величину:
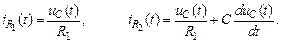
 и
и  в первое и четвертое уравнения и запишем получившуюся систему в операторной форме:
в первое и четвертое уравнения и запишем получившуюся систему в операторной форме:


 — коэффициент передачи,
— коэффициент передачи,  ,
,  — постоянные времени.
— постоянные времени.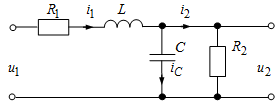

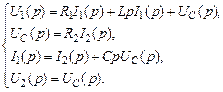

 в третье уравнение:
в третье уравнение:
 ;
;

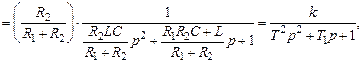
 ,
, 
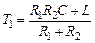 — постоянные времени.
— постоянные времени. ) и входного сопротивления (
) и входного сопротивления ( ).
).

 .
.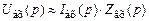 . Кроме того, учитывая, что
. Кроме того, учитывая, что  , следовательно,
, следовательно,  . Тогда выходное напряжение схемы может быть рассчитано по формуле
. Тогда выходное напряжение схемы может быть рассчитано по формуле .
.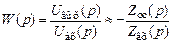 . (2.9)
. (2.9) и индуктивности
и индуктивности  рассчитываются по формулам
рассчитываются по формулам ,
,  .
. , для схемы, изображенной на рис. 2.7, а, получим:
, для схемы, изображенной на рис. 2.7, а, получим: ,
,  .
.
 — коэффициент передачи,
— коэффициент передачи,  — постоянная времени.
— постоянная времени.


