
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Передаточная функция. Амплитудно-частотная, фазово-частотная и амплитудно-фазовая характеристикаСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
В теории управления передаточная функция непрерывной системы представляет собой отношение преобразования Лапласа выходного сигнала к преобразованию Лапласа входного сигнала при нулевых начальных условиях. Зная входной сигнал системы и передаточную функцию, можно восстановить выходной сигнал. Пусть
где
В ТАУ наиболее часто используют следующие частотные характеристики: · амплитудная частотная характеристика (АЧХ); · фазовая частотная характеристика (ФЧХ); · амплитудно-фазовая частотная характеристика (АФЧХ). Амплитудная частотная характеристика (АЧХ) – зависимость отношения амплитуд выходного и входного сигналов от частоты
Фазовая частотная характеристика ФЧХ – зависимость фазового сдвига между входным и выходным сигналами от частоты. ФЧХ показывает, какое отставание или опережение выходного сигнала по фазе создает элемент при различных частотах. Амплитудную и фазовую характеристики можно объединить в одну общую – амплитудно-фазовую частотную характеристику (АФЧХ). АФЧХ представляет собой функцию комплексного переменного jw: W(jw) = A(w) e jj (w) (показательная форма) где A(w) – модуль функции; j (w) – аргумент функции. Основные понятия и принцип использования логарифмических и частотных характеристик. Частотные характеристики описывают передаточные свойства элементов и САУ в режиме установившихся гармонических колебаний, вызванных внешним гармоническим воздействием. Они находят применение в ТАУ, так как реальные возмущения, а следовательно и реакции на них элемента или САУ могут быть представлены как сумма гармонических сигналов. В ТАУ наиболее часто используют следующие частотные характеристики: · амплитудная частотная характеристика (АЧХ); · фазовая частотная характеристика (ФЧХ); · амплитудно-фазовая частотная характеристика (АФЧХ). Амплитудная частотная характеристика (АЧХ) – зависимость отношения амплитуд выходного и входного сигналов от частоты
Фазовая частотная характеристика ФЧХ – зависимость фазового сдвига между входным и выходным сигналами от частоты. ФЧХ показывает, какое отставание или опережение выходного сигнала по фазе создает элемент при различных частотах. Амплитудную и фазовую характеристики можно объединить в одну общую – амплитудно-фазовую частотную характеристику (АФЧХ). АФЧХ представляет собой функцию комплексного переменного jw: W(jw) = A(w) e jj (w) (показательная форма) где A(w) – модуль функции; j (w) – аргумент функции. При изменении частоты от нуля до бесконечности вектор W(jw) поворачивается вокруг начала координат, при этом одновременно изменяется длина вектора. Кривая, которую при этом опишет конец вектора, и есть АФЧХ. Каждой точке характеристики соответствует определенное значение частоты При практических расчетах САУ удобно использовать частотные характеристики, построенные в логарифмической системе координат. Такие характеристики называют логарифмическими. Они имеют меньшую кривизну и поэтому могут быть приближенно заменены ломаными линиями, составленными из нескольких прямолинейных отрезков. Причем, эти отрезки в большинстве случаев удается построить без громоздких вычислений при помощи некоторых простых правил. Кроме того, в логарифмической системе координат легко находить характеристики различных соединений элементов, так как умножению и делению обычных характеристик соответствует сложение и вычитание ординат логарифмических характеристик. За единицу длины по оси частот логарифмических характеристик принимают декаду. Декада – интервал частот, заключенный между произвольным значением частоты wi и его десятикратным значением 10wi. Отрезок логарифмической оси частот, соответствующий одной декаде, равен 1. Обычно в расчетах используют логарифмическую амплитудную частотную характеристику (ЛАЧХ) L(w) = 20 lgA(w) ординаты которой измеряют в логарифмических единицах – беллах (Б) или децибеллах (дБ).
|
||||
|
Последнее изменение этой страницы: 2016-06-29; просмотров: 458; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.148.105.152 (0.007 с.) |

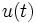 — входной сигнал линейной стационарной системы, а
— входной сигнал линейной стационарной системы, а  — её выходной сигнал. Тогда передаточная функция
— её выходной сигнал. Тогда передаточная функция  такой системы записывается в виде:
такой системы записывается в виде: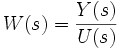 ,
, и
и  — преобразования Лапласа для сигналов
— преобразования Лапласа для сигналов  ,
, 




