
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Методика составления диф. уравнений авт. рег. системСодержание книги
Поиск на нашем сайте
Системы автоматического регулирования в большинстве случаев являются сложными устройствами, динамика которых описывается совокупностью' дифференциальных уравнений. Для получения этой совокупности необходимо составить дифференциальное уравнение для каждого элемента автоматической системы так, чтобы общее число уравнений было не меньше, чем число независимых обобщенных координат, определяющих состояние системы. При составлении дифференциального уравнения каждого элемента необходимо прежде всего выявить физический закон, определяющий его поведение. Таким законом может быть, например, закон сохранения вещества {объектат регулирования уровня, давления), закон сохранения энергии {объекты регулирования температуры), закон равновесия моментов (объекты регулирования скорости или угла поворота), закон равновесия электродвижущих сил (электрические цепи) и другие основные законы физики. Математическое выражение соответствующего физического закона и является исходным дифференциальным уравнением данного элемента автоматической системы. Например, для электродвигателя закон равновесия моментов на его валу может быть записан в следующем виде:
тде После записи дифференциального уравнения необходимо определить факторы, от которых зависят переменные, входящие в это уравнение. Для приведенного выше примера необходимо установить, от каких величин зависят и какими выражениями определяются вращающий момент двигателя Дальнейшим шагом является линеаризация полученных уравнений, если линеаризация вообще является допустимой. Обычно линеаризация допустима, если отсутствуют разрывные, неоднозначные или резко изгибающиеся характеристики и уравнения справедливы в течение всего интервала времени регулирования. В результате линеаризации получается совокупность дифференциальных уравнений, описывающих движение рассматриваемой системы. Введя алгебраизированный оператор дифференцирования
где
Совокупность (5.1) может быть решена относительно любой обобщенной координаты. Обычно она решается либо относительно отклонения регулируемой величины от заданного значения, т. е. ошибки Первый случай встречается чаще, так как исследованпе изменения ошибки, как правило, является более важным. В этом случае получается дифференциальное уравнение
Полином
где коэффициенты. Полином
где воздействия Полином на характер изменения ошибки Равным образом в системах программного регулирования и в следящих системах равенство Из (5.2) вытекает, что ошибка системы автоматического регулирования может быть представлена в виде суммы двух составляющих. Первая составляющая определяется наличием.задающего воздействия При решении системы дифференциальных уравнений относительно регулируемой величины Это уравнениеможет быть получено в результате подстановки выражения для ошибки
Степень этого полинома
Как уже говорилось выше, в системах автоматической стабилизации при чить При заданных функциях времени в правых частях дифференциальных уравнений (5.2) и (5.5) эти уравнения могут быть решены (проинтегрированы) относительно искомых функций времени, т. е. может быть найдено изменение ошибки регулирования во времени регулируемого объекта вместе с регулятором Уравнения (5.1) могут быть также представлены в форме Коши, т. е. в виде совокупности Здесь ваемые фазовые координаты системы, мущающие воздействия, а коэффициенты Если в (5.6) ввести алгебраизированный оператор и обозначить
8. Диф уравнения систем автоматического регулирования с нелинейностями В системах автоматического управления различают два вида нелинейностей: статические и динамические. Динамические нелинейности – это нелинейности дифференциальных уравнений, описывающих звено, например, (y ′(t)) 2 = kx(t). В наиболее распространенных случаях нелинейные свойства системы в основном определяются наличием в системе статических нелинейностей. Автоматические системы с существенными нелинейностями обладают рядом принципиальных особенностей, которые не присущи линейным системам и не могут быть выявлены при исследовании линеаризованного уравнения системы. Главные особенности этих систем вытекают из их неподчиненияпринципу суперпозиции: 1. Колебания переходного процесса в нелинейных системах могут отличаться от входного гармонического сигнала как по форме, так и по частоте. Например, для нелинейного элемента со статической характеристикой yнэ (x) =| x | при подаче на него входного сигнала x(t) = A sin ωt выходные колебания не являются гармоническими, они имеют совершенно другую форму и период вдвое меньший, чем период входных колебаний. Здесь частотные характеристики существенно зависят от амплитуды входного сигнала, т.е. M нэ (ω, A), φнэ (ω, A). В нелинейных системах условия устойчивости зависят от величины внешнего воздействия: система устойчива при одних значениях воздействий и неустойчива при других его значениях. Здесь нельзя говорить однозначно, устойчива система или нет. Для некоторых нелинейных систем, имеющих зону нечувствительности, наблюдается континиум состояний равновесия. Таким образом, в нелинейных системах говорят только об устойчивости конкретного состояния равновесия – устойчиво оно или нет. Весь строй мышления меняется, так как при одних внешних воздействиях переходной процесс сходится, а при других расходится. В связи с этим для нелинейных систем применяют понятие "устойчивость в малом", "устойчивость в большом", "устойчивость в целом". В нелинейных системах могут существовать собственные особые движения, получившие название автоколебаний. Автоколебания – это устойчивые собственные колебания, возникающие из-за нелинейных свойств системы при особых условиях. Режим автоколебаний принципиально отличается от колебаний линейной системы на границе устойчивости. В общем случае автоколебания в нелинейных системах нежелательны, а иногда и недопустимы. Однако, следует отметить, что в некоторых нелинейных системах автоколебания являются основным рабочим режимом.
|
||||
|
Последнее изменение этой страницы: 2016-06-29; просмотров: 282; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 13.58.110.182 (0.007 с.) |


 и
и  — приведенный момент инерции и угловая скорость двигателя,
— приведенный момент инерции и угловая скорость двигателя,  — вращающий момент двигателя,
— вращающий момент двигателя,  — тормозной момент внешних сил (момент нагрузки).
— тормозной момент внешних сил (момент нагрузки). и тормозной момент
и тормозной момент  на его валу. Нужно также выяснить, является ли приведенный момент инерции постоянной величиной или он изменяется в функции какой-либо переменной (например, в функции угла поворота двигателя).
на его валу. Нужно также выяснить, является ли приведенный момент инерции постоянной величиной или он изменяется в функции какой-либо переменной (например, в функции угла поворота двигателя). , эту совокупность можно представить в виде
, эту совокупность можно представить в виде (5.1)
(5.1) — обобщенные координаты системы, в том числе и регулируемая величина
— обобщенные координаты системы, в том числе и регулируемая величина 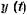 и ошибка
и ошибка  — функции времени, представляющие собой задающие и возмущающие воздействия. В дальнейшем без потери общности рассуждений будем считать, что к системе приложены только два воздействия — задающее воздействие
— функции времени, представляющие собой задающие и возмущающие воздействия. В дальнейшем без потери общности рассуждений будем считать, что к системе приложены только два воздействия — задающее воздействие 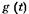 и возмущающее воздействие
и возмущающее воздействие  Например, можно положить, что
Например, можно положить, что 
 Кроме того, в (5.1) введены некоторые полиномы
Кроме того, в (5.1) введены некоторые полиномы  от оператора
от оператора 
 либо относительно регулируемой величины
либо относительно регулируемой величины 
 (5.2)
(5.2) степени
степени  от оператора
от оператора  характеризует свободное движение регулируемого объекта с регулятором. Он называется характеристическим полиномом и может быть представлен в виде
характеризует свободное движение регулируемого объекта с регулятором. Он называется характеристическим полиномом и может быть представлен в виде (5.3)
(5.3) в линеаризованной системе представляют собой постоянные
в линеаризованной системе представляют собой постоянные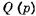 той же степени
той же степени (5.4)
(5.4) — постоянные коэффициенты, определяют влияние задающего
— постоянные коэффициенты, определяют влияние задающего на характер изменения ошибки
на характер изменения ошибки  . Под задающим воздействием
. Под задающим воздействием  здесь понимается требуемый закон изменения регулируемой величины
здесь понимается требуемый закон изменения регулируемой величины  . Выражение
. Выражение 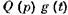 не равно нулю только в случае программного регулирования и в следящих системах. В системах автоматической стабилизации
не равно нулю только в случае программного регулирования и в следящих системах. В системах автоматической стабилизации  . Поэтому всегда можно выбрать начало отсчета так, чтобы
. Поэтому всегда можно выбрать начало отсчета так, чтобы  что упрощает выражение (5.2).
что упрощает выражение (5.2). определяет влияние возмущающего воздействия
определяет влияние возмущающего воздействия 
 . В уравнении (5.2) учтено одно возмущение
. В уравнении (5.2) учтено одно возмущение  , действующее на систему регулирования. В принципе таких возмущений может быть несколько. Однако вследствие линейности действует принцип суперпозиции и достаточно рассмотреть методику учета только одного возмущения; при наличии нескольких возмущений необходимо лишь просуммировать результат. Если для какого-либо возмущающего воздействия
, действующее на систему регулирования. В принципе таких возмущений может быть несколько. Однако вследствие линейности действует принцип суперпозиции и достаточно рассмотреть методику учета только одного возмущения; при наличии нескольких возмущений необходимо лишь просуммировать результат. Если для какого-либо возмущающего воздействия  полином
полином  , то говорят, что система автоматического регулирования является инвариантной относительно этого воздействия.
, то говорят, что система автоматического регулирования является инвариантной относительно этого воздействия. означает, что система является инвариантной относительно задающего воздействия.
означает, что система является инвариантной относительно задающего воздействия. . Вторая составляющая определяется наличием возмущающего воздействия (в общем случае — возмущающих воздействий или начальных условий). В системах автоматической стабилизации ошибка сводится только ко второй составляющей, т. е. определяется только наличием возмущающих воздействий.
. Вторая составляющая определяется наличием возмущающего воздействия (в общем случае — возмущающих воздействий или начальных условий). В системах автоматической стабилизации ошибка сводится только ко второй составляющей, т. е. определяется только наличием возмущающих воздействий. получается так называемое уравнение движения регулируемого объекта при наличии автоматического регулирования.
получается так называемое уравнение движения регулируемого объекта при наличии автоматического регулирования. в уравнение (5.2):
в уравнение (5.2): (5.5)
(5.5)

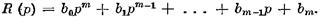
 можно при соответствующем выборе начала отсчета полу-
можно при соответствующем выборе начала отсчета полу- , что упрощает выражение (5.5).
, что упрощает выражение (5.5). из (5.2) и движение
из (5.2) и движение из (5.5).
из (5.5).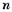 уравнений первого порядка, где
уравнений первого порядка, где  — порядок полинома
— порядок полинома  :
: 
 , в отличие от (5.1), представляют собой так назы-
, в отличие от (5.1), представляют собой так назы- — задающие и воз-
— задающие и воз- и
и 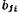 суть вещественные числа.
суть вещественные числа.
 , то эта совокупность уравнений может быть разрешена относительно любой из фазовых координат
, то эта совокупность уравнений может быть разрешена относительно любой из фазовых координат  .
.


