
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Математические методы анализа систем математического регулированияСодержание книги
Поиск на нашем сайте
Л.о.р. зі сталими коєфіціентами вищих порядків.
Якщо ki не кратні, то 1.1.Усі ki дійсні 1.2. є комплексні k уі=еkix k1=α+βi k2=α-βi c1y1+c2y2=eα(c1cosβ+c2sinβ)
2.1. Усі ki дійсні 2.2. є комплексні k k1=k2…=kr k1=k2…=kr= α+βi y1=ek1x k(r+1)=…k(2r)= α-βi y2=xek2x y1=eαxcosβx … … yr=xr-1ekrx yr= xr-1eαxcosβx … y(r+1)=eαxsinβx yn=eknx … y(2r)= xr-1eαxsinβx
4. Преобразования Лапласа и его свойства Преобразова́ние Лапла́са — интегральное преобразование, связывающее функцию Определение 1. Будем действительную функцию действительного аргумента f (t) называть оригиналом, если она удовлетворяет трем требованиям: 1. f (t) º 0, при t < 0. 2. f (t) < M*e^s 0 t, при t > 0, где M > 0, s 0>=0 — некоторые действительные постоянные, s 0 называют показателем роста функции f (t). В этом случае говорят, что функция f (t) возрастает не быстрее показательной функции. 3. На любом конечном отрезке [ a, b ] положительный полуоси Ot функция f (t) удовлетворяет условиям Дирихле, т.е. a) ограничена, b) либо непрерывна, либо имеет лишь конечное число точек разрыва I рода, c) имеет конечное число экстремумов. Функции, удовлетворяющие этим трем требованиям, называются в операционном исчислении изображаемыми по Лапласу или оригиналами. Определение 2. Изображением по Лапласу функции f (t) называется функция комплексного переменного p = s + is, определяемая соотношением
Пусть F(p):→f(t), G(p):→g(t) 5.1. Свойство линейности. Для любых комплексных постоянных a и b: αF (p) + βG (p):® αf (t) + βg (t) (12) 5.2. Теорема подобия. Для любого постоянного a > 0: 5.3. Теорема запаздывания. 5.4. Теорема смещения. Для a >0 имеет место соотношение: 5.5. Теорема упреждения. При а > 0 имеет место соотношение: 5.6.Теорема умножения изображений. . 5.7. Интеграл Дюамеля
5.8. Умножение оригиналов
5.9. Изображение периодических оригиналов
5.10. Дифференцирование оригинала
5.11. Дифференцирование изображения
5.12. Интегрирование оригинала
5.13. Интегрирование изображения
Предельные теоремы операционного исчисления и их применение
§ Запаздывание оригиналов и изображений. Предельные теоремы Запаздывание изображения:
Запаздывание оригинала:
H (x) — функция Хевисайда.
Теоремы о начальном и конечном значении (предельные теоремы):
Теорема о конечном значении очень полезна, так как описывает поведение оригинала на бесконечности с помощью простого соотношения. Это, например, используется для анализаустойчивости траектории динамической системы.
Линеаризация слабых нелинейностей Достаточно часто встречаются звенья, имеющие нелинейную зависимость между входной и выходной координатами. Если для малых отклонений от установившегося режима нелинейность несущественна, то в этом случае до составления исходных ДУ САР (1),..., (5) выполняют процедуру линеаризации. Суть линеаризации
1. Пусть нелинейное динамическое уравнение звена имеет вид: F(x1, x2, x2', y, y', y'', y''') = φ(f, f '). 2. Тогда уравнение установившегося состояния, всилу равенства нулю всех производных, имеет вид: Fo(x1o, x2o, 0, yo, 0, 0, 0) = φ(f o, 0). 3. Перейдем к уравнению динамики для отклонений, выполнив подстановки: x1 = x1o+Δx1(t), x2 = x2o+Δx2(t), x2' = Δx2'(t), и разложив функцию F в ряд:
4. Завершая линеаризацию, вычтем из левой и правой части уравнение установившегося состояния: (*)
Особенности линеаризованного уравнения 1. Оно является приближенным - отброшены члены высшего порядка малости. 2. Неизвестными функциями являются не полные величины, а их отклонения Δ... от установившихся значений. 3. Уравнение является линейным относительно отклонений Δ..., при этом масштабирующие коэффициенты (частные производные) могут быть постоянными или переменными во времени. 4. Внешнее воздействие линеаризации не подлежит.
Соединение сумматоров усилителей интеграторов и дифференциаторов. Векторы состояния. Отдельные блоки (звенья) систем автоматического регулирования могут быть соединены в различных комбинациях. Различают при основных типа соединения: - последовательное; - параллельное; - антипараллельное (с обратной связью). Рассмотрим каждое из типов соединения блоков системы. Основные понятия и принцип использования логарифмических и частотных характеристик.
Частотные характеристики описывают передаточные свойства элементов и САУ в режиме установившихся гармонических колебаний, вызванных внешним гармоническим воздействием. Они находят применение в ТАУ, так как реальные возмущения, а следовательно и реакции на них элемента или САУ могут быть представлены как сумма гармонических сигналов. В ТАУ наиболее часто используют следующие частотные характеристики: · амплитудная частотная характеристика (АЧХ); · фазовая частотная характеристика (ФЧХ); · амплитудно-фазовая частотная характеристика (АФЧХ). Амплитудная частотная характеристика (АЧХ) – зависимость отношения амплитуд выходного и входного сигналов от частоты
Фазовая частотная характеристика ФЧХ – зависимость фазового сдвига между входным и выходным сигналами от частоты. ФЧХ показывает, какое отставание или опережение выходного сигнала по фазе создает элемент при различных частотах. Амплитудную и фазовую характеристики можно объединить в одну общую – амплитудно-фазовую частотную характеристику (АФЧХ). АФЧХ представляет собой функцию комплексного переменного jw: W(jw) = A(w) e jj (w) (показательная форма) где A(w) – модуль функции; j (w) – аргумент функции. При изменении частоты от нуля до бесконечности вектор W(jw) поворачивается вокруг начала координат, при этом одновременно изменяется длина вектора. Кривая, которую при этом опишет конец вектора, и есть АФЧХ. Каждой точке характеристики соответствует определенное значение частоты При практических расчетах САУ удобно использовать частотные характеристики, построенные в логарифмической системе координат. Такие характеристики называют логарифмическими. Они имеют меньшую кривизну и поэтому могут быть приближенно заменены ломаными линиями, составленными из нескольких прямолинейных отрезков. Причем, эти отрезки в большинстве случаев удается построить без громоздких вычислений при помощи некоторых простых правил. Кроме того, в логарифмической системе координат легко находить характеристики различных соединений элементов, так как умножению и делению обычных характеристик соответствует сложение и вычитание ординат логарифмических характеристик. За единицу длины по оси частот логарифмических характеристик принимают декаду. Декада – интервал частот, заключенный между произвольным значением частоты wi и его десятикратным значением 10wi. Отрезок логарифмической оси частот, соответствующий одной декаде, равен 1. Обычно в расчетах используют логарифмическую амплитудную частотную характеристику (ЛАЧХ) L(w) = 20 lgA(w) ординаты которой измеряют в логарифмических единицах – беллах (Б) или децибеллах (дБ). Основные законы регулирования (П, Пи, ПИД). Изменение поведения систем при использовании регуляторов по временной области В составе структуры САР содержится управляющее устройство, которое называется регулятором и выполняет основные функции управления, путем выработки управляющего воздействия U в зависимости от ошибки (отклонения), т.е. U = f(D). Закон регулирования определяет вид этой зависимости без учёта инерционности элементов регулятора. Закон регулирования определяет основные качественные и количественные характеристики систем. Различают линейные и нелинейные законы регулирования. Кроме того, законы регулирования могут быть реализованы в непрерывном виде или в цифровом.
Рассмотрим основные линейные законы регулирования. В зависимости от вида преобразования ошибки регулирующие устройства можно подразделить на три основных типа: - пропорциональные (П-регуляторы); - интегральные (И-регуляторы); - дифференциальные (Д-регуляторы), а также их сочетания. Например, пропорционально-интегральные (ПИ- регуляторы), пропорционально-дифференциальные (ПД-регуляторы) и так далее. Передаточные функции регулирующих устройств имеют следующий вид. Интегральные регуляторы.
В интегральном регуляторе регулирующее воздействие пропорционально интегралу от ошибки регулирования. Регуляторы На практике широкое распространение получили типовые или промышленные регуляторы, представляющие собой универсальные автоматические устройства, легко приспосабливаемые для автоматизации разнообразных технологических процессов и объектов. При этом объект управления, как правило, является звеном статического типа, т.е. Wоу(0)=kоу, где kоу - коэффициент передачи объекта управления. Типовые регуляторы реализуют типовые законы управления, являющиеся частными случаями линейного стандартного закона управления, и классифицируются следующим образом. П-регуляторы. Реализуют П-закон или пропорциональный закон управления И-регуляторы. Реализуют И-закон или интегральный закон управления ПИ-регуляторы. Реализуют ПИ-закон или пропорционально-интегральный закон управления ПД-регуляторы. Реализуют ПД-закон или пропорционально-диф-ференциальный закон управления ПИД-регуляторы. Реализуют ПИД-закон или пропорционально-интегрально- дифференциальный закон управления, соответствующий линейному стандартному закону вида. В общем случае закон управления может иметь сложный вид. Корректирующие устройства Основная задача корректирующих устройств состоит в улучшении точности системы и качества переходных процессов. Однако наряду с этим путем дополнительного введения в систему корректирующих устройств решается более общая задача - обеспечение устойчивости системы, если она была неустойчивой, а затем и желаемого качества процесса управления. Различают три вида основных корректирующих устройств (последовательные, параллельные корректирующие устройства, обратные связи). Использование того или иного вида корректирующих устройств, т.е. последовательных звеньев, параллельных звеньев или обратных связей, определяется удобством технической реализации.
Примеры поведения систем с нечеткой логикой.
Одним из основных направлений практическоrо использования систем нечеткоro вывода является решение задач управления различными объектами или процессами. В этом случае построение нечеткой модели основывается на формальном представлении характеристик исследуемой системы в терминах линrвистических переменных. Поскольку кроме алrоритма управления, основными понятиями систем управления являются входные и выходные переменные, то именно они рассматриваются как линrвистические переменные при формировании базы правил в системах нечеткоrо вывода. В общем случае цель управления заключается в том, чтобы на основе анализа текущеrо состояния объекта управления определить значения управляющих переменных, реализация которых позволяет обеспечить желаемое поведение или состояние объекта управления. В настоящее время для решения соответствующих задач используется общая теория управления, в рамках которой разработаны различные алrоритмы нахождения оптимальных законов управления объектами различной физической природы. Математические методы анализа систем математического регулирования Основными элементами САУ являются: - объект управления (ОУ); - управляющее устройство или регулятор (Р), который сравнивает выход управляемого объекта с желаемым и в зависимости от этого вырабатывает управляющий сигнал на объект.
- Управляющие воздействия u1,..., um - это входные сигналы объекта управления, с помощью которых можно влиять на режим работы объекта.
- Выходные переменные y1,..., ym - это измеряемые выходные сигналы динамической системы. - Переменные состояния x1,..., xn - это внутренние, как правило, недоступные измерению переменные, которые определяют состояние объекта в каждый момент времени; причем n>=m. - Возмущающие воздействия M1,..., Ml - отражают случайные воздействия окружающей среды на объект управления и обычно недоступны измерению. Требование парирования их влияния и приводит к необходимости создания систем автоматического управления.
Входные воздействия на систему (или задание на регулятор) принято обозначать буквой v. Их число обычно совпадает с числом выходных переменных и изображается следующим вектором:
В зависимости от числа входных и выходных переменных выделяют: - одноканальные объекты (или системы) - объекты, в которых есть только одна выходная переменная (m =1); - многоканальные (многосвязные, многомерные, взаимосвязные) объекты (или системы) - объекты, в которых число выходных переменных больше единицы (m >1). Методы анализаСАУ включают в себя: - машинно-ориентированные традиционные методы анализа САУ (алгебраические, частотные, гармонической и статистической линеаризации):
- специально машинные методы, основанные на представлении процессов анализа САУ последовательностью реализуемых на ВМ операций над исходными и промежуточными числовыми данными; эти методы практически непригодны при отсутствии ЭВМ; - машинно-аналитические методы, необходимым условием применения которых также является наличие ЭВМ, но в отличие от Предыдущих промежуточные и конечные результаты исследования могут быть получены не в числовой, а в аналитической форме. С середины 50-х годов они использовались для построения амплитудно-фазовых частотных характеристик (АФЧХ), областей -разбиения, корневых годографов. Традиционно анализ САУ сводится к анализу устойчивости, качества и точности. Устойчивость - свойство системы, характеризующее способность возвращаться в равновесное состояние после снятия внешних сил, которые вывели её из этого состояния. Устойчивость системы определяют по переходным характеристикам или по импульсным функциям. Временные оценки качества Эти оценки на практике осуществляются численными методами, при этом по исходной ММ САУ строится численный переходный процесс в ней, по которому и делаются нужные оценки. При машинной ориентации численных методов преимущества ЭВМ становятся особенно очевидными, причем в этом случае уже нет необходимости в предварительной линеаризации исходной системы. Линейные многоканальные объекты обычно описывают системой дифференциальных уравнений первого порядка, представленной в векторно-матричном виде: Здесь Выходные переменные объекта изменяются в соответствии с уравнением выхода y = Cx(2.2) где Уравнения (2.1) и (2.2) описывают линейный стационарный объект. Если его параметры меняются с течением времени, то такой объект называется нестационарным, а математическая модель имеет вид (2.1)-(2.2), где элементы матриц являются функциями времени: A=A(t); B=B(t); C=C(t). Для описания одноканального объекта обычно используется скалярное дифференциальное уравнение: Наиболее простое (каноническое) описание получается в случае, когда в качестве переменных состояния выбирается выходная переменная y и ее производные до (n-1) включительно При этом вместо (2.3) имеем систему уравнений в виде нормальной формы Коши,
которая соответствует векторно-матричным уравнениям (2.1) и (2.2). Здесь матрицы A, B и C имеют вид:
причем Переход к описанию (2.1) - (2.2) не является однозначным: для одного объекта можно выбрать множество переменных состояния; важно, чтобы они были линейно - независимыми. При этом будут получаться различные матрицы объекта A, B и C. В общем случае одноканальный объект может описываться дифференциальным уравнением вида: т которого также можно перейти к векторно-матричным уравнениям типа (2.1) - (2.2). Таким образом, в качестве динамической характеристики линейных объектов управления используются дифференциальные уравнения, которые могут быть представлены в форме (2.1) - (2.2), (2.3), (2.4) или (2.5).
Якщо y1, y2,…yn – лінійно-незалежні розв’язки,то y=∑ciyi - розв’язок.
|
|||||||||
|
Последнее изменение этой страницы: 2016-06-29; просмотров: 390; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.139.80.107 (0.015 с.) |




 комплексного переменного (изображение) с функцией
комплексного переменного (изображение) с функцией 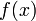 вещественного переменного (оригинал). С его помощью исследуются свойства динамических систем и решаются дифференциальные и интегральные уравнения.
вещественного переменного (оригинал). С его помощью исследуются свойства динамических систем и решаются дифференциальные и интегральные уравнения. (1)
(1)

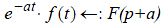







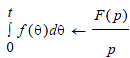





 , все полюсы в левой полуплоскости.
, все полюсы в левой полуплоскости.
 .
. .
.
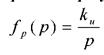
 Рассмотрим подробнее объект управления и выделим переменные, которые его характеризуют.
Рассмотрим подробнее объект управления и выделим переменные, которые его характеризуют. - Входными (задающими) принято называть воздейсвия (сигналы), поступающие на вход системы и определяющие требуемые законы изменения выходных переменных (сигналов)
- Входными (задающими) принято называть воздейсвия (сигналы), поступающие на вход системы и определяющие требуемые законы изменения выходных переменных (сигналов) Все переменные, которые характеризуют объект, удобно представить в векторной форме:
Все переменные, которые характеризуют объект, удобно представить в векторной форме:
 (2.1)
(2.1) - вектор состояния, n - порядок объекта;
- вектор состояния, n - порядок объекта;  - вектор управляющих воздействий,
- вектор управляющих воздействий,  A - квадратная матрица коэффициентов; B - прямоугольная матрица коэффициентов. Уравнения (2.1) называются дифференциальными уравнениями состояния.
A - квадратная матрица коэффициентов; B - прямоугольная матрица коэффициентов. Уравнения (2.1) называются дифференциальными уравнениями состояния. - вектор выхода; C - прямоугольная матрица коэффициентов.
- вектор выхода; C - прямоугольная матрица коэффициентов. (2.3), которое также может быть приведено к описанию типа (2.1) и (2.2) после соответствующего выбора линейно-независимых переменных состояния.
(2.3), которое также может быть приведено к описанию типа (2.1) и (2.2) после соответствующего выбора линейно-независимых переменных состояния.
 (2.4)
(2.4)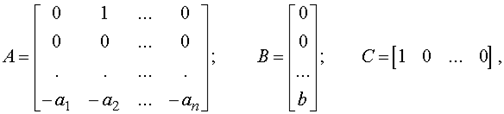


 , якщо f(x)=0 то рів-ня лінійне однорідне
, якщо f(x)=0 то рів-ня лінійне однорідне


