
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Показатели качества управления в статическом режиме работы САУ. Статические и астатические системыСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте Как всякая динамическая система, САУ может находиться в одном из двух режимов — стационарном (установившемся) и переходном. Стационарный режим может быть двух типов: статический и динамический. Ограничимся здесь рассмотрением лишь статического режима. В статическом режиме, при котором все внешние воздействия и параметры системы не меняются, качество управления характеризуется точностью. Рассмотрим САУ с двумя воздействиями: задающим
Рис. 5.1 — Структурная схема одноконтурной САУ
В соответствии с принципом суперпозиции линейная непрерывная САУ в операторной форме описывается уравнением динамики:
где
передаточные функции замкнутой системы по каждому из воздействий. Для анализа поведения САУ в статическом режиме (при
где Пусть система, изображенная на рис 5.1, не содержит интегрирующих звеньев, тогда
По уравнению (5.3) можно построить статические характеристики САУ. В зависимости от характера изменения воздействий Регулировочная статическая характеристика определяет изменение значения выходной величины при изменении величины задающего воздействия и при постоянном возмущающем воздействии, т.е., например, при
Эта характеристика изображена на рис. 5.2, а и представляет собой прямую, проходящую через начало координат под углом
Рис. 5.2 — Регулировочная (а) и внешняя (б) статические характеристики
Внешняя статическая характеристика (рис. 5.2, б) определяет изменение значения выходной величины при изменении величины возмущающего воздействия при постоянном задающем воздействии и рассчитывается непосредственно по формуле (5.3) при
где Величина
называется статической ошибкой системы и является основной величиной, определяющей точностные параметры САУ. В различных областях техники точность в установившемся (статическом) режиме принято характеризовать величиной отклонения выходной координаты в полном диапазоне изменения возмущающего воздействия в следующем виде: – абсолютной величиной отклонения – относительной величиной отклонения, выраженной в процентах
– статизмом внешней характеристики, выраженным в процентах
где Наличие статической ошибки в общем случае является нежелательным, т.к. создается погрешность управления. Для ее полного устранения, согласно формуле (5.5), требуется до бесконечности увеличивать коэффициент передачи Вместе с тем имеется путь устранения статической ошибки при конечной величине коэффициента передачи В статическую САУ (рис. 5.1) введем интегрирующее звено, например с единичным коэффициентом передачи, причем так, чтобы оно находилось между точками приложения задающего и возмущающего воздействий. Уравнение динамики системы будет выглядеть следующим образом:
При
Отсюда следует, что при включении интегрирующего звена на оговоренном выше участке системы удалось полностью ликвидировать статическую ошибку, т.е. получить Пусть теперь интегрирующее звено включено после точки приложения возмущения, например содержится в звене с передаточной функцией
При
то есть система остается статической. Системы, в которых при стремлении возмущающего воздействия к постоянной величине отклонение выходной величины стремится к нулю и не зависит от величины приложенного воздействия, называются астатическими. Изложенное выше позволяет сделать следующий вывод. Система будет астатической только в том случае, если интегрирующее звено будет включено на участке структурной схемы САУ между точками приложения задающего и возмущающего воздействий. Включение его после точки приложения возмущающего воздействия не делает систему астатической. Можно также показать, что введение интегрирующего звена в цепь обратной связи делает систему вообще неработоспособной, поскольку знаменатель ее передаточных функций при Порядок астатизма Если возмущающее воздействие изменяется во времени, то в САУ с астатизмом второго порядка ( Исключение статической и других (скоростной, по ускорению и т.д.) является несомненным достоинством астатических систем. Однако им присущ и ряд недостатков. 1. При введении интегрирующих звеньев снижается частота среза, сужается полоса пропускания средних частот, а как следствие – снижение быстродействия САУ. Расширить полосу пропускания и увеличить быстродействие астатической системы можно путём введения в неё не интегрирующих, а изодромных звеньев с передаточной функцией 2. Повышение порядка астатизма снижает устойчивость САУ, и, например при двух интегрирующих звеньях, она может стать структурно неустойчивой. Рассмотрим эту ситуацию на конкретном примере. Пусть в системе, структурная схема которой изображена на рис. 5.1, заданы следующие передаточные функции: Для повышения устойчивости астатических систем высокого порядка вместо интегрирующих звеньев также целесообразнее использовать изодромные звенья, позволяющие устранить нулевые коэффициенты в характеристическом полиноме. При соответствующем подборе постоянной времени 3. Присутствие оператора Лапласа Устранить этот недостаток можно, с одной стороны, подбором параметров астатической САУ, а с другой – повышением порядка её астатизма.
Пример 5.1 Рассчитать статическую точность системы стабилизации выходного напряжения генератора постоянного тока (рис. 1.3) для следующих параметров и воздействий: Прежде всего необходимо составить уравнение статики рассматриваемой системы. Не зная передаточных функций отдельных элементов и системы в целом, составим математическое описание для установившегося режима на основе статических характеристик отдельных элементов (примем допущение, что все элементы имеют линейные статические характеристики). В разомкнутой системе (см. рис. 1.2), как было выведено в разделе 1,
ЭДС генератора пропорциональна току возбуждения, т.е. С учетом этого соотношение (а) можно записать в следующем виде:
Уравнению (б) соответствует структурная схема, представленная на рис. 5.3, а. В замкнутой системе (см. рис. 1.3) часть выходного напряжения сравнивается с задающим и разность этих напряжений подается на вход усилителя У, в соответствии с чем можно записать
где С учетом формулы (в) на основе структурной схемы разомкнутой системы составим структурную схему замкнутой системы, как показано на рис. 5.3, б. В соответствии с правилами преобразования структурных схем для схемы, изображенной на рис. 5.3, б, получим уравнение
Уравнение статики (г), как видим, полностью соответствует обобщенному уравнению (5.3), отличаясь лишь обозначениями. Подставим в уравнение (г) заданные значения величин и определим максимальное
Рис. 5.3 — Пример статического расчета САУ
Представим выходное напряжение в форме (5.6):
Таким образом, при изменении в оговоренном диапазоне возмущающего воздействия (тока нагрузки) отклонение выходного напряжения не превысит величины ±1,84% от номинального значения.
|
||
|
Последнее изменение этой страницы: 2016-12-13; просмотров: 937; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.102 (0.012 с.) |

 и возмущающим
и возмущающим  , где
, где  — амплитуды этих воздействий. Структурная схема такой системы приведена на рис. 5.1.
— амплитуды этих воздействий. Структурная схема такой системы приведена на рис. 5.1.
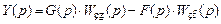 , (5.1)
, (5.1) — изображения задающего и возмущающего воздействий;
— изображения задающего и возмущающего воздействий; ,
, —
— ), в соответствии с теоремой операционного исчисления о конечном значении оригинала [1—3]
), в соответствии с теоремой операционного исчисления о конечном значении оригинала [1—3]  , в уравнении (5.1) в передаточных функциях и изображениях нужно принять
, в уравнении (5.1) в передаточных функциях и изображениях нужно принять  . При этом уравнение динамики превратится в уравнение статики вида
. При этом уравнение динамики превратится в уравнение статики вида , (5.2)
, (5.2) — текущие значения задающего и возмущающего воздействий.
— текущие значения задающего и возмущающего воздействий. , где
, где  — коэффициент передачи разомкнутой цепи,
— коэффициент передачи разомкнутой цепи, 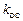 — коэффициент передачи звена обратной связи,
— коэффициент передачи звена обратной связи,  — коэффициент передачи разомкнутой САУ по возмущающему воздействию (звена
— коэффициент передачи разомкнутой САУ по возмущающему воздействию (звена 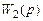 , установленного после точки приложения этого воздействия). Тогда уравнение (5.2) можно представить в виде:
, установленного после точки приложения этого воздействия). Тогда уравнение (5.2) можно представить в виде: . (5.3)
. (5.3) и
и  различают регулировочные и внешние статические характеристики.
различают регулировочные и внешние статические характеристики. регулировочную характеристику можно рассчитать по выражению:
регулировочную характеристику можно рассчитать по выражению: .
. , где
, где  — коэффициент передачи замкнутой системы по задающему воздействию.
— коэффициент передачи замкнутой системы по задающему воздействию.
 :
: , (5.4)
, (5.4) — коэффициент передачи замкнутой системы по возмущающему воздействию.
— коэффициент передачи замкнутой системы по возмущающему воздействию. (5.5)
(5.5) , где под номинальным значением
, где под номинальным значением  понимают усредненное значение выходной величины;
понимают усредненное значение выходной величины; (%); (5.6)
(%); (5.6)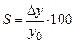 (%),
(%),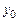 — значение выходной величины на холостом ходу (при
— значение выходной величины на холостом ходу (при 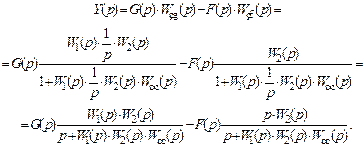
 получим
получим .
.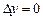 .
. . Тогда
. Тогда
 ,
, 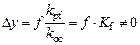 ,
, САУ определяется количеством интегрирующих звеньев, включенных между точками приложения задающего и возмущающего воздействий.
САУ определяется количеством интегрирующих звеньев, включенных между точками приложения задающего и возмущающего воздействий. ) нулю будет равна не только статическая ошибка, но и ошибка по первой производной от воздействия — скоростная ошибка. В системах с астатизмом третьего порядка, помимо перечисленных, нулю будет также равна ошибка по второй производной — ошибка по ускорению. Это свойство широко используется в следящих системах, системах с программным управлением, иначе, при нарастании задающего или возмущающего воздействий, скоростная ошибка будет также нарастать, а при сколько-нибудь длительном воздействии это недопустимо. Статическими могут быть только системы стабилизации.
) нулю будет равна не только статическая ошибка, но и ошибка по первой производной от воздействия — скоростная ошибка. В системах с астатизмом третьего порядка, помимо перечисленных, нулю будет также равна ошибка по второй производной — ошибка по ускорению. Это свойство широко используется в следящих системах, системах с программным управлением, иначе, при нарастании задающего или возмущающего воздействий, скоростная ошибка будет также нарастать, а при сколько-нибудь длительном воздействии это недопустимо. Статическими могут быть только системы стабилизации.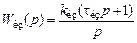 . Форсирующее звено, входящее в структуру изодромного звена, поднимет ЛАЧХ и ЛФЧХ САУ, увеличивая тем самым частоты среза и переворота фазы и расширяя полосу пропускания.
. Форсирующее звено, входящее в структуру изодромного звена, поднимет ЛАЧХ и ЛФЧХ САУ, увеличивая тем самым частоты среза и переворота фазы и расширяя полосу пропускания. ,
,  ,
,  . Тогда передаточная функция её разомкнутой цепи
. Тогда передаточная функция её разомкнутой цепи 
 , характеристический полином САУ
, характеристический полином САУ  , т.е.
, т.е.  ,
,  ,
,  ,
,  , главный минор определителя Гурвица для системы 3-го порядка
, главный минор определителя Гурвица для системы 3-го порядка  будет отрицательным при любых положительных значениях коэффициентов
будет отрицательным при любых положительных значениях коэффициентов  и
и  , и система будет структурно неустойчивой.
, и система будет структурно неустойчивой. включение изодромного звена не оказывает или почти не оказывает влияния на запасы устойчивости САУ. Таким путем можно обеспечить астатизм второго, третьего и более высокого порядка.
включение изодромного звена не оказывает или почти не оказывает влияния на запасы устойчивости САУ. Таким путем можно обеспечить астатизм второго, третьего и более высокого порядка. во втором слагаемом формулы (5.7) соответствует умножению изображения возмущающего воздействия
во втором слагаемом формулы (5.7) соответствует умножению изображения возмущающего воздействия  на этот оператор. Благодаря этому статическая ошибка в астатической системе и становится равной нулю. В то же время умножение изображения на
на этот оператор. Благодаря этому статическая ошибка в астатической системе и становится равной нулю. В то же время умножение изображения на  А/В;
А/В;  В/А;
В/А;  ;
;  Ом;
Ом;  В;
В;  А.
А. . (а)
. (а) , где
, где 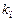 — коэффициент пропорциональности, зависящий от материала магнитопровода генератора, конструктивных особенностей генератора и т.д. Ток возбуждения
— коэффициент пропорциональности, зависящий от материала магнитопровода генератора, конструктивных особенностей генератора и т.д. Ток возбуждения 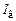 , в свою очередь, пропорционален входному сигналу усилителя У, т.е.
, в свою очередь, пропорционален входному сигналу усилителя У, т.е.  , где
, где  — коэффициент передачи функционального усилителя У.
— коэффициент передачи функционального усилителя У. . (б)
. (б) , (в)
, (в) — коэффициент передачи делителя.
— коэффициент передачи делителя. . (г)
. (г) и минимальное
и минимальное 
 значения выходного напряжения, соответствующие минимальному
значения выходного напряжения, соответствующие минимальному  А и максимальному
А и максимальному  А токам нагрузки:
А токам нагрузки: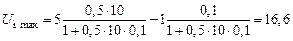 В;
В; В.
В.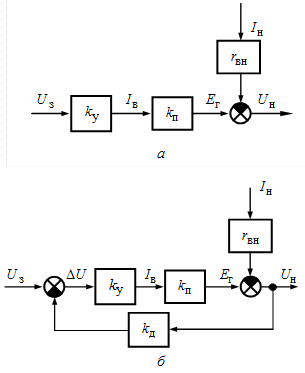
 В;
В; В;
В; %.
%.


