
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Статически неопределимые системы.Содержание книги
Поиск на нашем сайте 8.1. Определение перемещений с помощью интегралов Мора. Правило Верещагина Задача 8.1.1: Для представленного на рисунке криволинейного стержня приведены выражения углов поворота сечений В, С, D, Е соответственно. При их определении учтено только влияние изгибающего момента. Укажите неправильный ответ, если
1) 4) Решение: 1) Ответ верный. Балка состоит из двух участков: 2) Ответ неверный! Вероятно, ошибка связана с неправильным составлением выражений изгибающего момента М для криволинейного и прямолинейного участков. 3) Ответ неверный! Вероятно, неправильно выбраны пределы интегрирования. Проверьте чтобы на грузовом и единичном состояниях угол отсчитывался от одного и того же сечения в одном направлении. 4) Ответ неверный! Вероятно, ошибка связана с неправильным построением функций изгибающих моментов. Нужно составить интеграл Мора для участка АС, так как на остальных участках изгибающий момент в единичном состоянии равен нулю. Задача 8.1.2: Плоская рама нагружена, как показано на рисунке. Величины М, а, жесткость поперечного сечения на изгиб
1) Решение: 1) Ответ неверный! Обратите внимание, что длина горизонтального участка равна 2) Ответ неверный! При перемножении эпюр ординаты единичной эпюры, расположенные под центром тяжести грузовой, определены неверно. 3) Ответ верный. При вычислении интеграла Мора, воспользуемся способом Верищагина. Построим эпюру изгибающих моментов от внешних сил
4) Ответ неверный! При перемножении эпюр необходимо учесть, что площадь грузовой эпюры и ординаты единичной расположены по одну сторону от оси эпюры. Задача 8.1.3: Жесткость поперечного сечения на изгиб
1) Решение: 1) Ответ неверный! При перемножении эпюр неправильно определена площадь эпюры изгибающих моментов на втором участке. 2) Ответ неверный! Допущена ошибка при определении ординаты единичной эпюры на первом участке. 3) Ответ верный. При определении перемещения сечения В используем интеграл Мора, который вычислим по способу Верещагина. Обозначим участки балки индексами «1» и «2». Построим эпюру изгибающих моментов от внешних сил (эпюра построена на сжатом слое). 4) Ответ неверный! При перемножении эпюр неправильно определена ордината единичной эпюры на втором участке. Задача 8.1.4: Для балки, изображенной на рисунке, требуется определить абсолютное перемещение сечения А. Выражение … позволит наиболее точно определить данное перемещение.
1) 3) 4) Решение: 1), 4) Ответ неверный! Данное выражение для перемещения Таким образом, представленное выражение не позволит получить корректный результат. 2) Ответ верный. Данный случай нагружения соответствует случаю поперечного изгиба. Это означает, что внутренними силовыми факторами, оказывающими влияние на величину потенциальной энергии деформации, будут изгибающий момент (Мх) и поперечная сила (Qy). Остальные внутренние силовые факторы равны нулю. Представленное выражение учитывает их (Мх; Qy) совместное влияние и является правильным. 3) Ответ неверный! Несмотря на то, что данное выражение содержит 5 интегралов Мора, формула не учитывает вклад изгибающих моментов Мx в потенциальную энергию деформации. Кроме того, для данной расчетной схемы Му=Мz=N=Qx=0. Таким образом, представленное выражение не позволит получить корректный результат. 8.2. Статическая неопределимость. Степень статической неопределенности Задача 8.2.1: Число связей, при котором достигается кинематическая неизменяемость системы, носит название_______ связей. 1) дополнительных; 2) внутренних; 3) необходимого числа; 4) внешних. Решение: 1) Ответ неверный! Связи, наложенные на систему сверх необходимых, называют дополнительными. 2) Ответ неверный! Под внутренними понимают связи, действующие в поперечных сечениях систем. 3) Ответ верный. Положение жесткого тела в пространстве определяется шестью координатами, или, иначе, шестью степенями свободы. Следовательно, если на тело наложить определенным образом шесть связей, то положение его в пространстве будет определено полностью и система становится кинематически неизменяемой. Число связей, при котором достигается кинематическая неизменяемость системы, носит название необходимого числа связей. 4) Ответ неверный! Под внешними понимают связи, накладываемые на систему с помощью опор.
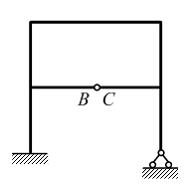
Задача 8.2.2: Степень статической неопределимости плоской рамы…
1) 0; 2) 2; 3) 3; 4) 1. Решение: 1) Ответ неверный! Степень статической неопределимости, равная нулю, означает, что система статически определима, то есть все опорные реакции и внутренние силовые факторы могут быть найдены с помощью уравнений статики. Если попробовать это сделать для данной рамы, то четырех уравнений равновесия будет явно недостаточно для нахождения шести неизвестных. 2) Ответ верный. Предположим, что шарнир отсутствует, тогда рама имеет три дополнительные внешние связи. 3) Ответ неверный! Очевидно, ошибка связана с тем, что упущен из виду шарнир С. Если бы его не было, то ответ был бы правильным. Шарнир, в котором сходятся два стержня, снимает одну связь и уменьшает на единицу степень статической неопределимости. 4) Ответ неверный! По-видимому, допущена ошибка при определении числа связей, снимаемых шарниром С. Нужно иметь в виду, что шарнир снимает одну связь (а не две). Существуют шарниры, в которых сходятся три и более стержней, тогда число снимаемых связей на единицу меньше числа сходящихся в нем стержней. Задача 8.2.3: Степень статической неопределимости плоской балки равна …
1) 3; 2) 1; 3) 2; 4) 0. Решение: 1) Ответ неверный! Видимо, ошибка связана с тем, что упущен из виду шарнир С. Если бы его не было, то ответ был бы правильным. Шарнир, в котором сходятся два стержня, снимает одну связь и уменьшает на единицу степень статической неопределимости. 2) Ответ неверный! По-видимому, допущена ошибка при определении числа связей, снимаемых шарниром С. Нужно иметь в виду, что шарнир снимает одну связь (а не две). Есть шарниры, в которых сходятся три и более стержней, тогда число снимаемых связей на единицу меньше числа сходящихся в нем стержней. 3) Ответ верный. Предположим, что шарнир С отсутствует, тогда балка имеет три дополнительные внешние связи, то есть три раза статически неопределима. Так как шарнир снимает одну связь, данная система является два раза статически неопределимой. 4) Ответ неверный! Степень статической неопределимости, равная нулю, означает, что система статически определима, то есть все опорные реакции и внутренние силовые факторы могут быть найдены с помощью уравнений статики. Если попробовать это сделать для данной рамы, то четырех уравнений равновесия будет явно недостаточно для нахождения шести неизвестных. Задача 8.2.4: Число дополнительных внутренних связей, наложенных на систему, равно …
1) 5; 2) 1; 3) 3; 4) 2. Решение: 1) Ответ неверный! В данном случае определено число внешних связей, наложенных на систему. 2) Ответ неверный! Ответ не соответствует условию задачи. Система имеет две дополнительные внутренние связи, запрещающие, например, взаимное вертикальное и горизонтальное смещения сечений, расположенных слева и справа от одиночного шарнира. 3) Ответ неверный! Полученное значение соответствует общему числу связей, наложенных на систему. 4) Ответ верный. Под внутренними связями понимаются ограничения, накладываемые на взаимные смещения элементов системы. Под внешними связями понимают условия, запрещающие абсолютные перемещения некоторых точек системы. Заделка в плоской системе накладывает три внешние связи, шарнирно-неподвижная опора – две. На систему кроме внешних связей наложены две дополнительные внутренние связи, например, запрещающие взаимное вертикальное и горизонтальное смещения сечений В и С.
Задача 8.2.5: Степень статической неопределимости для плоского замкнутого контура равна… 1) 2; 2) 3; 3) 1; 4) 4. Решение: 1), 3), 4) Ответ неверный! Проведите анализ количества внутренних связей в замкнутом контуре. 2) Ответ верный. В поперечном сечении плоского замкнутого контура имеют место три внутренние связи. Они запрещают взаимные два линейных перемещения и одно угловое двух сторон сечения. Поэтому степень статической неопределимости плоского замкнутого контура равна трем. Задача 8.2.6: Выберите неправильное определение понятия степени статической неопределимости. 1) Суммарное количество дополнительных внутренних и внешних связей; 2) Количество внешних и внутренних связей, наложенных на систему сверх необходимых.; 3) Количество дополнительных внутренних связей, наложенных на систему сверх необходимого для достижения ее кинематической неизменяемости. 4) Разница между числом неизвестных (реакций опор и внутренних силовых факторов) и числом независимых уравнений статики, которые могут быть составлены для рассматриваемой системы. Решение: 1) Ответ неверный! Всякая связь, наложенная на систему сверх необходимых, называется дополнительной (см. рис.1). 2) Ответ неверный! Число связей, при котором достигается кинематическая неизменяемость, называется необходимым числом связей. Под кинематически неизменяемой понимается такая система, положение которой в пространстве (как жесткого целого) однозначно определено. Всякая связь, наложенная сверх необходимых, называется дополнительной. 3) Ответ верный. Неправильное определение: количество дополнительных внутренних связей, наложенных на систему сверх необходимого для достижения ее кинематической неизменяемости . 4) Ответ неверный! Статически определимой называют систему, для которой все реакции опор могут быть определены с помощью уравнений равновесия, а затем методом сечений могут быть найдены внутренние силовые факторы в любом поперечном сечении. 8.3. Метод сил Задача 8.3.1: Число канонических уравнений, которое нужно составить и решить для раскрытия статической неопределимости, равно…
1) 4; 2) 2; 3) 1; 4) 3. Решение: 1), 3), 4) Ответ неверный! Проверьте правильность определения числа дополнительных связей, наложенных на систему. 2) Ответ верный. Степень статической неопределимости для плоской системы можно определить по формуле Задача 8.3.2: Система, освобожденная от дополнительных связей, статически определимая и кинематически неизменяемая, носит название… 1) системы с определенным числом степеней свободы; 2) расчетной схемы; 3) эквивалентной системы; 4) основной системы. Решение: 1) Ответ неверный! Под числом степеней свободы понимается число независимых координат, определяющих положение системы в пространстве. 2) Ответ неверный! Реальный объект, освобожденный от несущественных особенностей, носит название расчетной схемы. 3) Ответ неверный! Основная система в методе сил, к которой приложены неизвестные силы, моменты и внешние заданные нагрузки, называется эквивалентной системой. 4) Ответ верный. При раскрытии статической неопределимости стержневых, рамных систем используют, например, метод сил. Он заключается в том, что заданная статически неопределимая система освобождается от дополнительных связей, как внешних, так и внутренних, а их действие заменяется силами и моментами. Их величина в дальнейшем подбирается из условий, чтобы перемещения сечений соответствовали тем ограничениям, которые были наложены на систему отброшенными связями. Задача 8.3.3: Для плоской статически неопределенной рамы выбрана основная система метода сил и записаны канонические уравнения. Неправильным является следующее определение коэффициентов канонических уравнений:
1) 2) 3) 4) Решение: 1), 2), 3) Ответ неверный! Согласно идее метода сил коэффициенты 4) Ответ верный. Согласно идее метода сил коэффициенты Задача 8.3.4: Система канонических уравнений имеет вид 1) k -го силового фактора от внешних сил; 2) i -го силового фактора под действием единичной силы, заменяющей k -й фактор; 3) i -го силового фактора от заданной внешней нагрузки; 4) i -го силового фактора от неизвестной k -ой силы. Решение: 1) Ответ неверный! Индекс i в коэффициенте 2) Ответ неверный! Данный ответ соответствует перемещению 3) Ответ неверный! Необходимо вспомнить последовательность рассуждений при выводе системы канонических уравнений метода сил. 4) Ответ верный. На основании принципа независимости действия сил перемещение в направлении i -ой неизвестной силы равно сумме перемещений от действия всех неизвестных сил, внешней нагрузки и равно нулю, т.е. Задача 8.3.5: Для заданной статически неопределимой балки представлены четыре варианта основной системы метода сил. Неправильный ответ соответствует варианту...
1) 3) Решение: 1), 2), 3) Ответ неверный! Данная балка является два раза статически неопределимой системой. На нее наложены шесть связей (необходимых четыре). Таким образом, дополнительных связей две. 4) Ответ верный. Данная балка является два раза статически неопределимой системой. На нее наложены шесть связей (необходимых четыре). Таким образом, дополнительных связей две. 8.4. Расчет простейших статически неопределимых систем Задача 8.4.1: Стержень круглого сечения диаметром
1) Решение: 1) Ответ неверный! Допущена ошибка при определении коэффициента 2) Ответ неверный! Допущена ошибка при определении коэффициента 3) Ответ неверный! Напоминаем, что полярный момент сопротивления при кручении стержня с круглым сечением определяется по формуле 4) Ответ верный. При решении задачи используем метод сил. Отбросим дополнительную связь, например, в опоре А. Действие отброшенной связи заменим неизвестным моментом
Задача 8.4.2: Если
1) Решение: 1), 3) Ответ неверный! Вероятно, допущена ошибка в построении эпюр моментов. 2) Ответ неверный! Вероятно, неправильно найден коэффициент 4) Ответ верный. Система один раз статически неопределима. «Отбрасываем» одну связь (превращаем заделку в шарнирно-неподвижную опору), прикладываем вместо отброшенной связи момент Задача 8.4.3: Стержень нагружен силой F. Модуль упругости материала Е, площадь поперечного сечения А, размер
1) Решение: 1) Ответ неверный! Данное значение соответствует минимальному напряжению в стержне по абсолютной величине. 2) Ответ верный. Выбираем основную систему метода сил. Отбросим, например, дополнительную связь в опоре С и заменим ее действие неизвестной силой 3) Ответ неверный! При определении коэффициента 4) Ответ неверный! Допущена ошибка при определении коэффициента Задача 8.4.4: Для балки, представленной на рисунке, реакция опоры В равна…
1) Решение: 1) Ответ неверный! Допущена ошибка при вычислении коэффициента канонического уравнения 2) Ответ верный. Выбираем основную систему метода сил, отбрасываем дополнительную связь (опору В) и заменяем ее действие реакцией 3) Ответ неверный! Вероятно, допущена ошибка при «перемножении» единичной и грузовой эпюры. Нужно помнить, что по правилу Верещагина функции перемножают по отдельным участкам, на которых они однозначно определены. В данном случае эпюра от нагрузки задается на 2-х участках длиной l и 2l. Причем на последнем она равна нулю. 4) Ответ неверный! Допущена ошибка при вычислении коэффициента канонического уравнения
Задача 8.4.5: Если
1) Решение: 1) Ответ неверный! Видимо, ошибка связана с неправильным расчетом 2) Ответ неверный! Ошибка связана с неправильным расчетом коэффициента |
|
| Поделиться: |

 .
.
 ; 2)
; 2)  ; 3)
; 3)  ;
; .
. – прямолинейный, AD – криволинейный. Для решения задачи используется интеграл Мора
– прямолинейный, AD – криволинейный. Для решения задачи используется интеграл Мора  ,
,  – на криволинейном участке. На
– на криволинейном участке. На  , так как линия действия силы совпадает с
, так как линия действия силы совпадает с 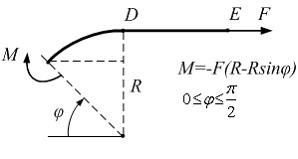
 необходимо приложить единичный момент в сечении В и составить выражение
необходимо приложить единичный момент в сечении В и составить выражение 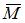 для участков АВ и BD соответственно.
для участков АВ и BD соответственно. ;
;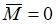 .
.
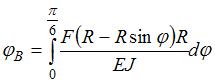 или
или 

 .
.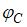 в формуле
в формуле  достаточно изменить пределы интегрирования, поскольку
достаточно изменить пределы интегрирования, поскольку  на участке АС.
на участке АС.  Для нахождения
Для нахождения  в формуле
в формуле 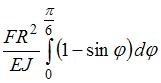 достаточно изменить пределы интегрирования, поскольку
достаточно изменить пределы интегрирования, поскольку  .
. 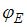 необходимо приложить единичный момент в т. Е, то появится еще
необходимо приложить единичный момент в т. Е, то появится еще  .
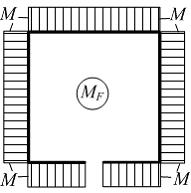
. заданы. Взаимное удаление сечений А и В равно…
заданы. Взаимное удаление сечений А и В равно…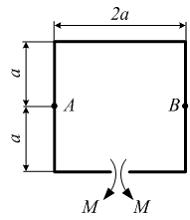
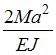 ; 2)
; 2)  ; 3)
; 3)  ; 4)
; 4) 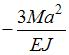 .
. .
. .
.

 , тогда
, тогда
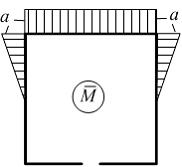
 задан. Значение силы F, при которой прогиб концевого сечения В будет f, равно …
задан. Значение силы F, при которой прогиб концевого сечения В будет f, равно …
 ; 2)
; 2)  ; 3)
; 3) 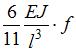 ; 4)
; 4)  .
.



 ; 2)
; 2)  ;
; ;
; .
. не учитывает вклад изгибающих моментов (Мх) в потенциальную энергию деформации балки. Отсутствует один из интегралов Мора
не учитывает вклад изгибающих моментов (Мх) в потенциальную энергию деформации балки. Отсутствует один из интегралов Мора  . Однако имеет место My. Анализ представленной схемы нагружения применительно к изображенной системе координат позволяет сделать вывод, что изгиба в плоскости xz не происходит, то есть
. Однако имеет место My. Анализ представленной схемы нагружения применительно к изображенной системе координат позволяет сделать вывод, что изгиба в плоскости xz не происходит, то есть  .
.






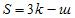 ,
,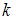 – число замкнутых контуров;
– число замкнутых контуров; ,
,  , тогда степень статической неопределимости системы
, тогда степень статической неопределимости системы  . Следовательно, при решении задачи методом сил надо отбросить две дополнительные связи и ввести две неизвестные силы. Число канонических уравнений в методе сил равно степени статической неопределимости системы, то есть равно двум.
. Следовательно, при решении задачи методом сил надо отбросить две дополнительные связи и ввести две неизвестные силы. Число канонических уравнений в методе сил равно степени статической неопределимости системы, то есть равно двум.
 – это перемещение по направлению силы
– это перемещение по направлению силы  под действием единичной силы, заменяющей силу
под действием единичной силы, заменяющей силу  – это перемещение по направлению силы
– это перемещение по направлению силы  ;
; – это перемещение по направлению силы
– это перемещение по направлению силы  – это перемещение по направлению силы
– это перемещение по направлению силы  , входящие в канонические уравнения, представляют собой перемещения.
, входящие в канонические уравнения, представляют собой перемещения. под действием единичного фактора, заменяющего
под действием единичного фактора, заменяющего  . Таким образом, определение является верным.
. Таким образом, определение является верным.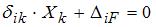 . Произведение
. Произведение  – это перемещение по направлению …
– это перемещение по направлению … означает, что речь идет о перемещении по направлению неизвестной силы
означает, что речь идет о перемещении по направлению неизвестной силы  .
.
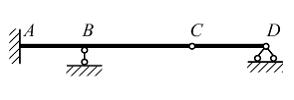
 можно записать в виде
можно записать в виде  .
.
 ; 2)
; 2)  ;
; ; 4)
; 4) 
 работает на деформацию кручение. Модуль сдвига материала
работает на деформацию кручение. Модуль сдвига материала  , размер
, размер  , значение
, значение  заданы. Наибольшее касательное напряжение равно…
заданы. Наибольшее касательное напряжение равно…
 ; 2)
; 2)  ; 3)
; 3) 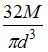 ; 4)
; 4)  .
. .
. .
.

 .
.
 ,
,



 .
. ,
,  , величина момента в заделке А равна …
, величина момента в заделке А равна …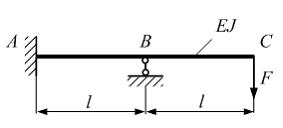
 ; 2) 0; 3)
; 2) 0; 3)  ; 4)
; 4)  .
.

 − искомый момент в заделке А.
− искомый момент в заделке А. 
 и грузовую
и грузовую  эпюры:
эпюры:

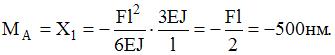

 ; 2)
; 2)  ; 3)
; 3)  ; 4)
; 4) 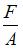 .
.


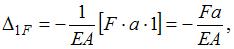
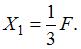



 ; 2)
; 2)  ; 3) 0; 4)
; 3) 0; 4)  .
.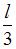 от заделки А.
от заделки А.
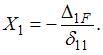


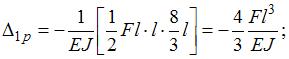

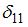 .
. саму на себя по правилу Верещагина. Нужно определить ее площадь
саму на себя по правилу Верещагина. Нужно определить ее площадь 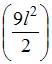 и умножить на ординату (2L), проходящую через ее центр тяжести.
и умножить на ординату (2L), проходящую через ее центр тяжести. , реакция опоры С для представленной плоской рамы равна …
, реакция опоры С для представленной плоской рамы равна …
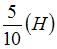 ; 2)
; 2)  ; 3)
; 3)  ; 4)
; 4)  .
. и ордината над ее центром тяжести на единичной эпюре
и ордината над ее центром тяжести на единичной эпюре  .
.



