
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Геометрические характеристики поперечных сечений стержняСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
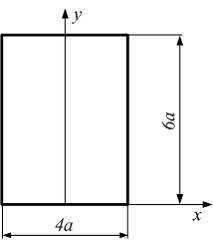
5.1. Статические моменты. Центр тяжести плоской фигуры Задача 5.1.1: Статический момент площади сечения относительно оси x равен…
1) 48а3; 2) 96а3; 3) 144а3; 4) 72а3. Решение: 1) Ответ неверный! Возможна ошибка в незнании понятия статического момента сечения относительно оси. 2) Ответ неверный! Возможна ошибка в выборе оси координат. 3) Ответ неверный! Возможна ошибка в определении ординаты центра тяжести сечения. 4) Ответ верный. Статический момент площади сечения относительно оси x
Задача 5.1.2: Ось, относительно которой статический момент площади сечения равен нулю, называется… 1) осью симметрии; 2) центральной; 3) средней линией контура; 4) нейтральной линией. Решение: 1) Ответ неверный! Ось симметрии делит сечение на две одинаковые фигуры. 2) Ответ верный. Рассмотрим некоторое поперечное сечение стержня. Свяжем его с системой координат x, y и составим два следующих интеграла: 3) Ответ неверный! Средняя линия разделяет толщину стенки контура на равные части. 4) Ответ неверный! Геометрическое место точек в поперечном сечении, где нормальные напряжения равны нулю, называется нейтральной линией. Задача 5.1.3: Статический момент площади сечения относительно оси x равен…
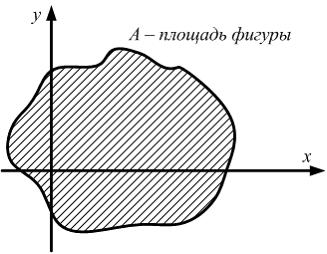
1) Решение: 1) Ответ неверный! Площади вырезов в формулу нужно подставлять со знаком «минус». 2) Ответ неверный! Возможна ошибка в выборе оси координат. 3) Ответ неверный! Возможно, ошибка вызвана незнанием понятия статического момента площади фигуры относительно оси. 4) Ответ верный. Статический момент сечения относительно оси x Задача 5.1.4: Статический момент площади фигуры относительно оси x определяется интегралом …
1) Решение: 1) Ответ верный.
2) Ответ неверный! Интеграл 3) Ответ неверный! Данный интеграл есть центробежный момент инерции площади сечения относительно осей x и y. 4) Ответ неверный! Данный интеграл называется моментом инерции площади относительно оси x. Задача 5.1.5: Статический момент площади сечения относительно оси x равен…
1) Решение: 1) Ответ неверный! Размерность статического момента площади сечения в системе СИ 2) Ответ верный. Центр тяжести треугольника расположен на расстоянии 3) Ответ неверный! Данное значение соответствует статическому моменту площади сечения относительно оси, совпадающей с основанием треугольника, когда положительное значение оси y направлено вверх. 4) Ответ неверный! Значение соответствует статическому моменту площади сечения относительно оси, проходящей через вершину треугольника параллельно основанию. Положительное направление оси y – вниз. 5.2. Осевые моменты инерции. Зависимость между моментами инерции при параллельном переносе осей Задача 5.2.1: Осевой момент инерции площади сечения относительно оси y равен…
1) Решение: 1) Ответ неверный! Возможно, допущена ошибка в выборе осей координат. 2) Ответ неверный! Допущена ошибка в использовании формулы для момента инерции круга. 3) Ответ верный. Для круга 4) Ответ неверный! Возможно, незнание понятия осевого момента инерции площади относительно оси. Задача 5.2.2: Осевой момент инерции площади фигуры относительно оси y определяется интегралом …
1) Решение: 1) Ответ неверный! Данный интеграл есть момент инерции площади относительно оси x. 2) Ответ неверный! Данный интеграл есть статический момент инерции площади относительно оси x. 3) Ответ верный.
Разделим площадь А плоской фигуры на элементарные площадки dA прямоугольной координатной сеткой (x и y – координаты центра тяжести элементарной площадки). Если каждую элементарную площадку умножить на
Аналогично определяется момент инерции относительно оси x. 4) Ответ неверный! Данный интеграл определяет статический момент инерции площади относительно оси y. Задача 5.2.3: На рисунке размеры поперечного сечения заданы в см. Осевой момент инерции сечения относительно центральной оси x равен…
1) Решение: 1) Ответ неверный! При вычислении не учтено, что два прямоугольника с размерами 2) Ответ неверный! Допущена ошибка при определении осевого момента инерции прямоугольного сечения относительно центральной оси, параллельной основанию. 3) Ответ неверный! Данное значение соответствует осевому моменту инерции прямоугольника 1 относительно центральной оси x. 4) Ответ верный. Дополним поперечное сечение до прямоугольника, который обозначим цифрой 1. Прямоугольнику с отрицательной площадью присвоим цифру 2. Ось Задача 5.2.4: Если
1) Решение: 1) Ответ неверный! Допущена ошибка в вычислениях. 2) Ответ неверный! Возможна ошибка в вычислении осевого момента инерции треугольника относительно оси x. 3) Ответ неверный! Возможна ошибка в использовании зависимости для вычисления осевого момента инерции при переходе к параллельной оси. 4) Ответ верный. Для вычисления Задача 5.2.5: Осевой момент инерции сечения относительно оси
1) Решение: 1) Ответ неверный! Допущена ошибка при определении площади поперечного сечения. 2) Ответ верный. Для круглого сечения диаметром 3) Ответ неверный! Данное выражение соответствует осевому моменту инерции сечения относительно центральной оси 4) Ответ неверный! Ошибка при определении осевого момента инерции сечения относительно центральной оси.
Задача 5.2.6: Осевой момент инерции площади сечения относительно оси y равен…
1) Решение: 1), 2), 4) Ответ неверный! Возможна ошибка в незнании понятия осевого момента инерции площади относительно центральной оси параллельной основанию прямоугольника, или незнанием формулы для осевого момента инерции прямоугольника. 3) Ответ верный. Для прямоугольника 5.3. Главные оси и главные моменты инерции Задача 5.3.1: Для сечения известны осевые моменты инерции сечения относительно осей
1) 1000 см2; 2) 2000 см2; 3) 2500 см2; 4) 3000 см2. Решение: 1) Ответ неверный! Осевой момент инерции сечения относительно оси 2) Ответ неверный! Допущена арифметическая ошибка при вычислениях. 3) Ответ верный. Сумма осевых моментов инерции сечения относительно двух взаимно перпендикулярных осей при повороте осей на некоторый угол остается постоянной, то есть 4) Ответ неверный! Необходимо вспомнить теоретические положения об изменении моментов инерции сечения при повороте осей координат на произвольный угол. Задача 5.3.2: Из указанных центральных осей сечения равнобокого уголка главными являются…
1) х3; 2) все; 3) х1; 4) х2. Решение: 1), 3) Ответ неверный! Ось х3 и х1 не является осями симметрии. 2) Ответ неверный! Осью симметрии является только ось х2. 4) Ответ верный. Для симметричных сечений оси симметрии являются главными осями инерции. Задача 5.3.3: Главные оси инерции … 1) можно провести только через точки, лежащие на оси симметрии; 2) можно провести только через центр тяжести плоской фигуры; 3) это оси, относительно которых моменты инерции плоской фигуры равны нулю; 4) можно провести через любую точку плоской фигуры. Решение: 1) Ответ неверный! В курсе сопротивления материалов доказывается, что через любую точку плоской фигуры можно провести две взаимно перпендикулярные оси, которые будут главными осями фигуры для этой точки. 2) Ответ неверный!
3) Ответ неверный! Момент инерции площади относительно любой оси есть величина положительная и не равная нулю. 4) Ответ верный.
На рисунке показана произвольная плоская фигура. Через точку С проведены две взаимно перпендикулярные оси U и V. В курсе сопротивления материалов доказывается, что если эти оси поворачивать, то можно определить такое их положение, при котором центробежный момент инерции площади обращается в ноль, а моменты инерции относительно этих осей принимают экстремальные значения. Такие оси называются главными осями. Две взаимно перпендикулярные оси, обладающие такими свойствами, можно провести через любую точку плоской фигуры. Задача 5.3.4: Из указанных центральных осей главными осями сечения являются…
1) все; 2) Решение: 1) Ответ верный. Для симметричных сечений оси симметрии являются главными осями инерции. 2), 3), 4) Ответ неверный! Другие оси тоже являются осями симметрии.
Задача 5.3.5: Оси, относительно которых центробежный момент инерции равен нулю, а осевые моменты принимают экстремальные значения, называются… 1) центральными осями; 2) осями симметрии; 3) главными центральными осями; 4) главными осями. Решение: 1) Ответ неверный! Центральными называются оси, проходящие через центр тяжести поперечного сечения. 2) Ответ неверный! Ось симметрии делит сечение на два одинаковых сечения. 3) Ответ неверный! Главные оси, если они являются центральными, называются главными центральными осями. 4) Ответ верный. При повороте осей координат моменты инерции сечения меняются.
Задача 5.3.6: Момент инерции сечения относительно главной центральной оси
1) Решение: 1) Ответ неверный! Моменты инерции вырезов при вычислениях нужно подставлять со знаком «минус». 2) Ответ верный.
Для вычисления 3) Ответ неверный! Возможно, допущена ошибка в использовании зависимости для вычисления осевого момента инерции при переходе к параллельной оси. 4) Ответ неверный! Возможно, допущена ошибка в вычислении осевых моментов инерции простейших фигур.
5.4. Моменты инерции простых и сложных сечений Задача 5.4.1: Осевой момент инерции сечения относительно оси
1) Решение: 1) Ответ неверный! Возможно, допущена ошибка при вычислении осевых моментов инерции составных фигур. 2) Ответ неверный! Возможно, допущена ошибка в формуле для осевого момента прямоугольника относительно центральной оси. 3) Ответ верный.
Осевой момент инерции 4) Ответ неверный! Возможно, допущена ошибка при разделении сечения на простейшие фигуры. Задача 5.4.2: Поперечное сечение балки составлено из вертикального листа и четырех неравнобоких уголков
1) 3) Решение: 1), 4) Ответ неверный! При определении осевого момента инерции сечения относительно оси x неправильно использованы формулы перехода к параллельным осям. 2) Ответ неверный! При вычислении осевого момента инерции сечения относительно оси y не учтен момент инерции прямоугольного сечения. 3) Ответ верный. При решении задачи воспользуемся формулами перехода к параллельным осям: Задача 5.4.3: Момент инерции площади фигуры, состоящей из двух кругов, относительно оси x равен…
1) Решение: 1) Ответ неверный! Площадь круга вычислена неверно. 2) Ответ неверный! При решении не учитывалось, что сечение состоит из двух кругов одинакового диаметра. 3) Ответ верный. При вычислении задачи используем формулу перехода к параллельным осям 4) Ответ неверный! При вычислении
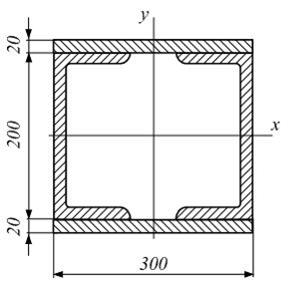
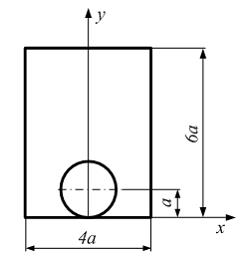
Задача 5.4.4: Момент инерции площади фигуры относительно оси x, проходящей через центр тяжести фигуры, равен …
1) Решение: 1) Ответ неверный! Совершенно необоснованно применена формула перехода к параллельным осям c межосевым расстоянием 2) Ответ неверный! По всей видимости, неправильно записана формула момента инерции квадрата относительно оси x. 3) Ответ неверный! По всей видимости, неправильно записана формула момента инерции круга относительно оси x. 4) Ответ верный.
Разбиваем фигуру на квадрат (фигура 1) и круг (фигура 2). Момент инерции всей фигуры равен разности моментов инерции квадрата и круга:
Задача 5.4.5: Поперечное сечение балки составлено из двух швеллеров №20 и листов, прикрепленных с помощью сварки. Характеристики швеллера приведены. Размеры на рисунке даны в мм. Осевой момент инерции сечения относительно главной центральной оси x равен…
1) Решение: 1) Ответ неверный! При вычислении осевого момента инерции сечения не учитывался осевой момент инерции прямоугольника относительно его главной центральной оси, параллелельной оси x. 2) Ответ неверный! При вычислении не учитывалось, что в сечении два швеллера и два прямоугольника. 3) Ответ неверный! Допущена ошибка при определении осевого момента инерции прямоугольного сечения относительно оси x. 4) Ответ верный. Разбиваем сложное сечение на ряд простых фигур: два швеллера и два прямоугольника, которые обозначены индексами 1 и 2 соответственно (рис.). Задача 5.4.6: Момент инерции сечения относительно оси
1) Решение: 1) Ответ неверный! Возможно, допущена ошибка в использовании зависимости для вычисления осевого момента инерции при параллельном переносе осей. 2) Ответ неверный! Моменты инерции вырезов подставляются в формулу со знаком «минус». 3) Ответ неверный! Возможно, допущена ошибка в вычислении осевых моментов инерции простейших фигур. 4) Ответ верный.
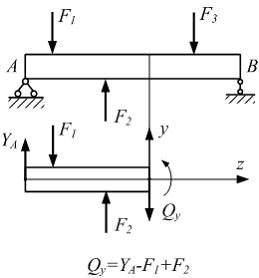
Для вычисления Плоский прямой изгиб 6.1. Поперечная сила, изгибающий момент и их эпюры Задача 6.1.1: Поперечная сила Qy в произвольном поперечном сечении стержня численно равна алгебраической сумме проекций на ось… 1) y всех внешних сил, расположенных по одну сторону от рассматриваемого сечения; 2) x всех внешних сил, действующих по одну сторону от рассматриваемого сечения; 3) y всех внешних сил, действующих на стержень; 4) y всех внешних и внутренних сил, действующих на стержень. Решение: 1) Ответ верный. Поперечная сила Qy в произвольном поперечном сечении стержня численно равна алгебраической сумме проекций на ось y всех внешних сил (в том числе и реакций внешних связей), расположенных по одну сторону от рассматриваемого сечения.
2) Ответ неверный! Допущена ошибка в понимании терминов «поперечная сила» и «продольная сила». Продольная сила N в произвольном поперечном сечении стержня равна алгебраической сумме проекций на ось x стержня всех внешних сил, расположенных по одну сторону от рассматриваемого сечения. Поперечная сила Qy равна алгебраической сумме проекций на ось y всех внешних сил, расположенных по одну сторону от рассматриваемого сечения. 3) Ответ неверный! Допущена ошибка в применении метода сечений. Метод сечений заключается в следующем. В пределах рассматриваемого участка, проводят сечение, перпендикулярное к оси стержня. Одну часть стержня отбрасывают. Действие отброшенной части на оставшуюся заменяют внутренними силовыми факторами, одним из которых является поперечная сила. Поперечную силу прикладывают таким образом, чтобы она вращала рассматриваемую часть относительной внутренней точки этой части по часовой стрелке. В этом случае поперечная сила считается положительной. Затем составляют уравнение равновесия для оставленной части. Следовательно, поперечная сила равна алгебраической сумме проекций на ось y всех внешних сил, приложенных по одну сторону от рассматриваемого сечения. 4) Ответ неверный! Допущена ошибка в применении метода сечений. Внутренние силы, или силы взаимодействия между частицами тела, всегда входят попарно, отличаясь друг от друга знаками. Поэтому геометрическая сумма всех внутренних сил в теле равна нулю. Следовательно, алгебраические суммы проекций внутренних сил на какую-либо ось также равны нулю. Задача 6.1.2: Балка нагружена равномерно распределенной нагрузкой интенсивности q. Эпюра изгибающих моментов имеет вид…
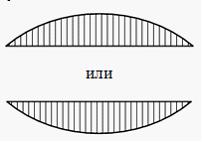
1) 3) Решение: 1), 2) Ответ неверный! Допущена ошибка в построении эпюры изгибающих моментов. При данном виде нагружения балки эпюра изгибающих моментов будет изменяться по закону квадратной параболы. 3) Ответ верный. При данном виде нагружения эпюра изгибающих моментов изменяется по закону квадратной параболы. В середине эпюры будет максимум. Эпюра в зависимости от того, на сжатом или растянутом слое балки она строится, будет иметь вид показанный на рисунке 3). 4) Ответ неверный! Допущена ошибка в построении эпюры изгибающих моментов. Построена эпюра для случая нагружения балки в середине пролета сосредоточенной силой. Задача 6.1.3: Эпюра изгибающих моментов имеет вид…
1) 3) Решение: 1) Ответ неверный! Допущена ошибка в построении эпюры изгибающих моментов. Такой вид эпюра имеет для случая нагружения балки равномерно распределенной нагрузкой. 2), 3) Ответ неверный! Допущена ошибка в построении эпюры изгибающих моментов. На рисунке представлена эпюра поперечных сил. 4) Ответ верный. При данном виде нагружения в пределах каждого участка эпюра изгибающих моментов изменяется по линейному закону. В точке приложения сосредоточенной силы должно быть изменение угла наклона эпюры (излом). Эпюра будет иметь вид, представленный на рисунке 4) в зависимости от того, на сжатом или растянутом слое она построена. Задача 6.1.4: Балка нагружена распределенной нагрузкой, меняющейся по закону
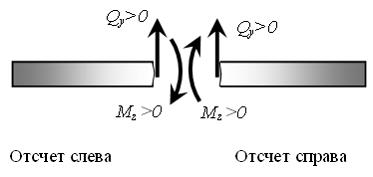
1) синуса; 2) косинуса; 3) прямой, параллельной оси балки; 4) прямой, наклонной к оси балки. Решение: 1) Ответ неверный! Допущена ошибка при использовании дифференциальных зависимостей при поперечном изгибе. Необходимо вспомнить, что интеграл от синуса будет равен минус косинус. 2) Ответ верный. Воспользуемся дифференциальными зависимостями при плоском поперечном изгибе 3) Ответ неверный! Поперечная сила изменяется по закону прямой, параллельной оси балки, в случае, когда на участке нет распределенной нагрузки. 4) Ответ неверный! Из дифференциальных зависимостей при плоском поперечном изгибе известно, что поперечная сила меняется по линейному закону тогда, когда на участке балки действует равномерно распределенная нагрузка. Задача 6.1.5: Правило знаков для поперечной силы Qy и изгибающего момента Мz изображено на рисунке… 1) 2) 3) 4) Решение: 1), 4) Ответ неверный! Не выполняется закон о равенстве действия и противодействия. Допущена ошибка в правиле знаков при применении метода сечений. Поперечную силу прикладывают таким образом, чтобы она вращала рассматриваемую часть по часовой стрелке. Она считается положительной, если вектор образует правую систему координат с вектором внешней нормали к сечению. Изгибающий момент считают положительным, если сжатый слой находится сверху (вогнутость балки направлена вверх). 2) Ответ неверный! Допущена ошибка в понимании терминов «поперечная сила» и «продольная сила». Продольная сила N в произвольном поперечном сечении стержня равна алгебраической сумме проекций на продольную ось стержня всех внешних сил, приложенных по одну сторону от рассматриваемого сечения. Поперечная сила Qy равна алгебраической сумме проекций на поперечную ось y всех внешних сил, приложенных по одну сторону от рассматрив
|
||||
|
Последнее изменение этой страницы: 2016-12-10; просмотров: 3950; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.191.178.16 (0.009 с.) |

 .
.  ,
, – ордината центра тяжести сечения.
– ордината центра тяжести сечения.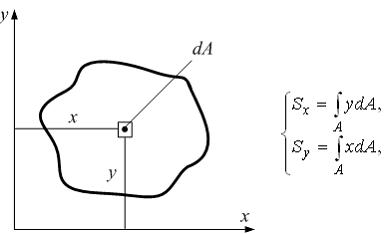

 ; 2) 0; 3)
; 2) 0; 3)  ; 4)
; 4)  .
. ,
, – ординаты центров тяжести составных фигур.
– ординаты центров тяжести составных фигур. .
.
 ; 2)
; 2)  ; 3)
; 3)  ; 4)
; 4)  .
.
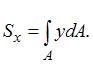 Аналогично определяется статический момент площади относительно оси y. Поскольку под интегралом координата у в первой степени, статический момент, в зависимости от выбора системы координат, может быть положительным, отрицательным или равным нулю.
Аналогично определяется статический момент площади относительно оси y. Поскольку под интегралом координата у в первой степени, статический момент, в зависимости от выбора системы координат, может быть положительным, отрицательным или равным нулю.
 ; 2) нулю; 3)
; 2) нулю; 3)  ; 4)
; 4)  .
. . По данной формуле определяется площадь треугольника.
. По данной формуле определяется площадь треугольника. от основания. Следовательно, ось x проходит через центр тяжести фигуры и является центральной. Относительно центральной оси статический момент площади сечения равен нулю.
от основания. Следовательно, ось x проходит через центр тяжести фигуры и является центральной. Относительно центральной оси статический момент площади сечения равен нулю.
 ; 2)
; 2) 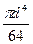 ; 3)
; 3)  ; 4)
; 4) 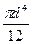 .
. . В данном случае для полукруга
. В данном случае для полукруга  .
.
 ; 2)
; 2)  ; 3)
; 3)  ; 4)
; 4)  .
. и сложить эти произведения, то получим осевой момент площади относительно оси y. Чем мельче координатная сетка, тем точнее результат расчета. Заменяя операцию сложения интегрированием по площади А, получим выражение для осевого момента площади относительно оси y:
и сложить эти произведения, то получим осевой момент площади относительно оси y. Чем мельче координатная сетка, тем точнее результат расчета. Заменяя операцию сложения интегрированием по площади А, получим выражение для осевого момента площади относительно оси y:

 ; 2)
; 2)  ; 3)
; 3)  ; 4)
; 4)  .
. имеют отрицательную площадь.
имеют отрицательную площадь.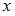 является центральной для прямоугольников 1 и 2.
является центральной для прямоугольников 1 и 2. 
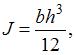 где b –ширина прямоугольника; h – высота.
где b –ширина прямоугольника; h – высота.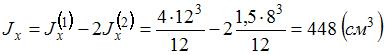 .
. , то значение осевого момента инерции площади относительно оси
, то значение осевого момента инерции площади относительно оси  равно…
равно…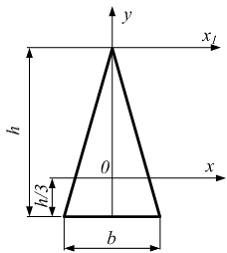
 ; 2)
; 2)  ; 3)
; 3)  ; 4)
; 4) 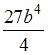 .
. используем формулу перехода от центральной оси к любой, параллельной ей:
используем формулу перехода от центральной оси к любой, параллельной ей:  .
. равен…
равен…
 ; 2)
; 2)  ; 3)
; 3) 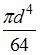 ; 4)
; 4)  .
. осевой момент инерции сечения относительно центральной оси х определяется по формуле
осевой момент инерции сечения относительно центральной оси х определяется по формуле  .
. расположена параллельно центральной. Воспользуемся формулой для определения осевого момента инерции сечения при переходе от центральной оси к нецентральной, расположенной параллельно центральной.
расположена параллельно центральной. Воспользуемся формулой для определения осевого момента инерции сечения при переходе от центральной оси к нецентральной, расположенной параллельно центральной.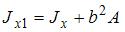 ,
,  – расстояние между осями
– расстояние между осями 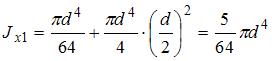 .
.
 ; 2)
; 2)  ; 3)
; 3)  ; 4)
; 4)  .
. – момент инерции площади относительно центральной оси, параллельной основанию: где b – основание, h – высота.
– момент инерции площади относительно центральной оси, параллельной основанию: где b – основание, h – высота. .
. ,
,  :
:  ,
,  ,
,  . Осевой момент инерции относительно оси
. Осевой момент инерции относительно оси  равен…
равен…
 в старой системе координат.
в старой системе координат. .
. .
.

 Следовательно оси x, y являются главными осями фигуры.
Следовательно оси x, y являются главными осями фигуры.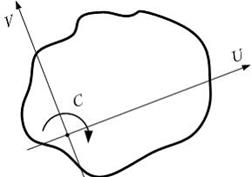

 ; 3)
; 3)  и
и  .
.
 ,
,  , повернутых на некоторый угол относительно осей
, повернутых на некоторый угол относительно осей  ,
, ,
, .
. центробежный момент инерции сечения обращается в нуль, а осевые моменты инерции принимают экстремальные значения. Данные оси называются главными осями.
центробежный момент инерции сечения обращается в нуль, а осевые моменты инерции принимают экстремальные значения. Данные оси называются главными осями. равен…
равен…
 ; 2)
; 2)  ; 3)
; 3)  ; 4)
; 4) 

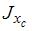 используем формулу
используем формулу 
 .
.
 ; 2)
; 2)  ; 3)
; 3)  ; 4)
; 4)  .
.
 . В данном случае
. В данном случае 
 . Характеристики уголка заданы. Размеры на рисунке даны в мм. Моменты инерции сечения
. Характеристики уголка заданы. Размеры на рисунке даны в мм. Моменты инерции сечения  и
и  соответственно равны…
соответственно равны…

 ; 2)
; 2)  ;
; ; 4)
; 4)  .
. ,
, ,
,
 .
.

 ; 2)
; 2)  ; 3)
; 3)  .
. – осевой момент инерции площади фигуры относительно своей центральной оси
– осевой момент инерции площади фигуры относительно своей центральной оси  .
. не учитывалось, что центральная ось круга не совпадает с осью x.
не учитывалось, что центральная ось круга не совпадает с осью x.
 ; 2)
; 2)  ; 3)
; 3)  ; 4)
; 4) 
 .
.


 ; 2)
; 2) 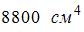 ; 3)
; 3)  ; 4)
; 4) 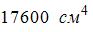 .
.
 ,
,  .
. Поэтому при определении момента инерции второй фигуры относительно оси x надо воспользоваться формулой перехода к параллельным осям. Окончательно имеем
Поэтому при определении момента инерции второй фигуры относительно оси x надо воспользоваться формулой перехода к параллельным осям. Окончательно имеем  .
.
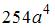 ; 2)
; 2)  ; 3)
; 3)  ; 4)
; 4)  .
.
 используем формулу
используем формулу 
 .
.

 ; 2)
; 2)  ;
; ; 4)
; 4)  .
.
 ; 2)
; 2)  ; 4)
; 4)  .
. . Поперечная сила по длине балки изменяется по закону …
. Поперечная сила по длине балки изменяется по закону …

 и q,составимвыражение для определения поперечной силы
и q,составимвыражение для определения поперечной силы  , или
, или
 ;
; ;
; ;
; .
.


