
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Напряженное состояние в точке. Главные площадки и главные напряженияСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Задача 4.1.1: Совокупность напряжений, возникающих на множестве площадок, проходящих через рассматриваемую точку, называют … 1) напряженным состоянием в точке; 2) полным напряжением; 3) нормальным напряжением; 4) касательным напряжением. Решение: 1) Ответ верный. Напряженное состояние в точке полностью определяется шестью компонентами тензора напряжений: σ x, σ y, σ z, τ xy, τ yz, τ zx. Зная эти компоненты, можно определить напряжения на любой площадке, проходящей через данную точку. Совокупность напряжений, действующих по множеству площадок (сечений), проходящих через данную точку, называется напряженным состоянием в точке.
2) Ответ неверный! Незнание определения полного напряжения в точке (сила, приходящаяся на единицу площади сечения). 3) Ответ неверный! Напомним, что проекция вектора полного напряжения на нормаль к сечению называется нормальным напряжением. 4) Ответ неверный! Допущена ошибка в определении термина «касательное напряжение». Задача 4.1.2: Площадки в исследуемой точке напряженного тела, на которых касательные напряжения равны нулю, называют … 1) ориентированными; 2) главными площадками; 3) октаэдрическими; 4) секущими. Решение: 1) Ответ неверный! Термин не соответствует заданному условию. Под ориентированными понимаются площадки, которые проходят через точку по заранее заданному направлению. 2) Ответ верный.
3) Ответ неверный! Термин не соответствует заданному условию. Октаэдрическими называют площадки равнонаклоненные к главным. Касательные напряжения на октаэдрических площадках не равны нулю. 4) Ответ неверный! Напоминаем, что под секущими понимают площадки проведенные через точку, в которой исследуется напряженное состояние. Задача 4.1.3: Главные напряжения для напряженного состояния, показанного на рисунке, равны… (Значения напряжений указаны в МПа).
1)σ1=150 МПа, σ2=50 МПа; 2) σ1=0 МПа, σ2=50 МПа, σ3=150 МПа; 3) σ1=150 МПа, σ2=50 МПа, σ3=0 МПа; 4) σ1=100 МПа, σ2=100 МПа, σ3=0 МПа; Решение: 1) Ответ неверный! Не указано значение главного напряжения σ3=0 МПа. 2) Ответ неверный! Обозначения главных напряжений не соответствуют правилу нумерации. 3) Ответ верный. Одна грань элемента свободна от касательных напряжений. Поэтому это главная площадка, а нормальное напряжение (главное напряжение) на этой площадке также равно нулю. 4) Ответ неверный! Это не главные напряжения, а заданные значения нормальных напряжений, действующие на выделенный элемент.
Задача 4.1.4: В исследуемой точке напряженного тела на трех главных площадках определены значения нормальных напряжений: 1)σ1=150 МПа, σ2=50 МПа, σ3=-100 МПа; 2) σ1=150 МПа, σ2=-100 МПа, σ3=50 МПа; 3) σ1=50 МПа, σ2=-100 МПа, σ3=150 МПа; 4) σ1=-100 МПа, σ2=50 МПа, σ3=150 МПа; Решение: 1) Ответ верный. Главным напряжениям присваивают индексы 1, 2, 3 так, чтобы выполнялось условие 2), 3), 4) Ответ неверный! Главным напряжениям присваивают индексы 1, 2, 3 так, чтобы выполнялось условие
Задача 4.1.5: На гранях элементарного объема (см. рисунок) определены значения напряжений в МПа. Угол между положительным направлением оси x и внешней нормалью к главной площадке, на которой действует минимальное главное напряжение, равен …
1) Решение: 1), 2), 4) Ответ неверный! По всей видимости, неправильно записана формула для определения угла. Правильная запись: 3) Ответ верный.
Задача 4.1.6: Значения главных напряжений определяют из решения кубического уравнения 1) инвариантами напряженного состояния; 2) упругими постоянными; 3) направляющими косинусами нормали; 4) коэффициентами пропорциональности. Решение: 1) Ответ верный. Корни уравнения – главные напряжения − определяются характером напряженного состояния в точке и не зависят от выбора исходной системы координат. Следовательно, при повороте системы осей координат коэффициенты 2) Ответ неверный! Ошибка в определении термина. Упругие постоянные характеризуют свойства материала. 3) Ответ неверный! Напомним, что направляющие косинусы – это косинусы углов, которые образует нормаль с осями координат. 4) Ответ неверный! Термин не соответствует условию вопроса
4.2. Виды напряженного состояния Задача 4.2.1: Стержень круглого сечения диаметром d испытывает деформации чистый изгиб и кручение. Напряженное состояние в точке В показано на рисунке…
1) Решение: 1) Ответ неверный! Крутящий момент вызывает появление касательных напряжений в плоскости перпендикулярной оси стержня. 2) Ответ неверный! Направление касательного напряжения в точке В поперечного сечения должно соответствовать направлению крутящего момента в данном сечении. 3) Ответ верный. Секущими плоскостями, ориентированными вдоль и поперек оси стержня, выделим объемный элемент. В сечении стержня у заделки действуют изгибающий момент М и крутящий момент 2М. От изгибающего момента М в точке В возникает нормальное растягивающее напряжение 4) Ответ неверный! От крутящего момента в точке В поперечного сечения возникает касательное напряжение Задача 4.2.2: Стержень испытывает деформации растяжение и чистый изгиб. Напряженное состояние, которое возникает в опасной точке, называется…
1) плоским; 2) объемным; 3) линейным; 4) чистым сдвигом. Решение: 1) Ответ неверный! При плоском напряженном состоянии одно значение главного напряжения равно нулю. 2) Ответ неверный! В опасной точке отлично от нуля только одно главное напряжение. При объемном напряженном состоянии отличны от нуля три главных напряжения. 3) Ответ верный. Опасные точки расположены бесконечно близко к верхней грани элемента. В них возникают только растягивающие нормальные напряжения от продольной силы и изгибающего момента. Эпюры распределения напряжений от каждого внутреннего силового фактора и результирующая эпюра показаны на рисунке. 4) Ответ неверный! При чистом сдвиге два главных напряжения равны, но противоположны по знаку, а третье равно нулю. Задача 4.2.3: Напряженное состояние «чистый сдвиг» показано на рисунке… 1) Решение: 1) Ответ неверный! На рисунке показано плоское напряженное состояние – двухосное растяжение. 2) Ответ неверный! Элемент находится в условиях плоского напряженного состояния – двухосного смешанного напряженного состояния. 3) Ответ верный.
Чистый сдвиг – напряженное состояние, когда на гранях выделенного элементарного объема действуют только касательные напряжения. Если элементарный объем повернуть на угол, равный 4) Ответ неверный! Данный элемент испытывает линейное напряженное состояние. Задача 4.2.4: Тип напряженного состояния, показанного на рисунке, называется…
1) линейным; 2) плоским; 3) объемным; 4) чистым сдвигом. Решение: 1) Ответ верный. Тип напряженного состояния определяется в зависимости от значений главных напряжений. В примере одна грань свободна от касательных напряжений – это главная площадка. Нормальное напряжение, действующее на главной площадке, называют главным напряжением. В данном случае оно равно нулю. Используя формулу 2) Ответ неверный! При плоском напряженном состоянии одно главное напряжение равно нулю. В данном случае два главных напряжения равны нулю. 3) Ответ неверный! При объемном напряженном состоянии 4) Ответ неверный! При чистом сдвиге
Задача 4.2.5: Напряженное состояние при значениях 1) объемным; 2) чистым сдвигом; 3) плоским; 4) линейным. Решение: 1) Ответ неверный! При объемном напряженном состоянии отличны от нуля все три главных напряжения. 2) Ответ неверный! При чистом сдвиге одно значение главного напряжения равно нулю, а два других равны по величине, но противоположны по знаку. 3) Ответ верный. Тип напряженного состояния определяется значениями главных напряжений. В случае, когда все три главных напряжения отличны от нуля, имеем объемное напряженное состояние. Если одно главное напряжение равно нулю - плоское напряженное состояние, а когда два равны нулю – линейное. Следовательно, в данном примере будет плоское напряженное состояние. 4) Ответ неверный! При линейном напряженном состоянии только одно главное напряжение отлично от нуля.
Задача 4.2.6: На гранях элементарного объема (см. рисунок) действуют напряжения заданные в МПа. Напряженное состояние в точке …
1) линейное; 2) плоское (чистый сдвиг); 3) плоское; 4) объемное. Решение: 1) Ответ неверный! Фронтальная грань элементарного объема свободна от касательных напряжений. Это означает, что данная грань является главной площадкой и одно из трех главных напряжений равно (-50 МПа). Два других главных напряжения определите по формуле 2) Ответ неверный! Напомним, что при чистом сдвиге одно из главных напряжений равно нулю. Два других равны по абсолютной величине и противоположны по знаку. 3) Ответ верный. Передняя грань элементарного объема свободна от касательных напряжений. Это означает, что она является главной площадкой и одно из трех главных напряжений равно (-50 МПа). Два других главных напряжения определим по формуле 4) Ответ неверный! Фронтальная грань элементарного объема свободна от касательных напряжений. Это означает, что данная грань является главной площадкой и одно из трех главных напряжений равно (-50 МПа). Два других главных напряжения можно определить по формуле
|
||||
|
Последнее изменение этой страницы: 2016-12-10; просмотров: 2373; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.141.46.108 (0.008 с.) |




 ,
,
 ,
,  ,
,  . После преобразований найдем
. После преобразований найдем 

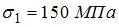 ,
, 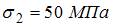 ,
, 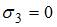 , т.е. плоское напряженное состояние.
, т.е. плоское напряженное состояние.

 Главные напряжения в этом случае равны...
Главные напряжения в этом случае равны... . Следовательно,
. Следовательно, 
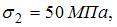


 ; 2)
; 2) 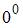 ; 3)
; 3)  ; 4)
; 4) 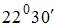 .
.


 определяется по формуле
определяется по формуле  Поскольку угол отрицательный, откладываем угол по часовой стрелке.
Поскольку угол отрицательный, откладываем угол по часовой стрелке. Коэффициенты
Коэффициенты  ,
,  ,
,  называют…
называют…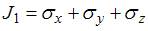

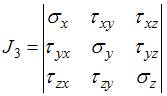

 ; 2)
; 2)  ; 3)
; 3)  ; 4)
; 4) 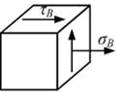 .
.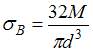 . Крутящий момент 2М, действующий в плоскости, перпендикулярной оси стержня, вызывает касательное напряжение
. Крутящий момент 2М, действующий в плоскости, перпендикулярной оси стержня, вызывает касательное напряжение  . Направление касательного напряжения должно быть согласовано с направлением крутящего момента. Поэтому напряженное состояние элемента на рисунке 4 соответствует напряженному состоянию в точке В.
. Направление касательного напряжения должно быть согласовано с направлением крутящего момента. Поэтому напряженное состояние элемента на рисунке 4 соответствует напряженному состоянию в точке В. . Направление касательного напряжения должно быть согласовано с направлением крутящего момента.
. Направление касательного напряжения должно быть согласовано с направлением крутящего момента. 


 ; 2)
; 2)  ; 3)
; 3)  ; 4)
; 4)  .
.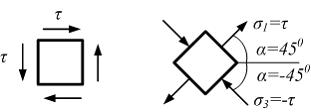
 , то касательные напряжения на его гранях (площадках) будут равны нулю, но появятся нормальные (главные) напряжения
, то касательные напряжения на его гранях (площадках) будут равны нулю, но появятся нормальные (главные) напряжения  и
и  . Таким образом, чистый сдвиг может быть реализован растяжением и сжатием в двух взаимно перпендикулярных направлениях напряжениями, равными по абсолютной величине.
. Таким образом, чистый сдвиг может быть реализован растяжением и сжатием в двух взаимно перпендикулярных направлениях напряжениями, равными по абсолютной величине.
 , найдем два других главных напряжения. После преобразований получим
, найдем два других главных напряжения. После преобразований получим  ,
,  . В соответствии с принятыми обозначениями имеем
. В соответствии с принятыми обозначениями имеем  ,
, 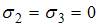 . Два главных напряжения равны нулю. Следовательно, на рисунке показано линейное напряженное состояние.
. Два главных напряжения равны нулю. Следовательно, на рисунке показано линейное напряженное состояние.

 В данном случае два главных напряжения равны нулю. Поэтому данное напряженное состояние не является объемным.
В данном случае два главных напряжения равны нулю. Поэтому данное напряженное состояние не является объемным. ,
, 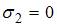 . Расчеты показывают, что для данного случая это неверно.
. Расчеты показывают, что для данного случая это неверно.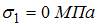 ,
,  ,
,  называют…
называют…







