
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Деформированное состояние в точке. Связь между деформациями и напряжениямиСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Задача 4.4.1: Зависимость между компонентами напряженного и деформированного состояния в пределах малых упругих деформаций носит название… 1) принципа Сен-Венана; 2) закона Гука при сдвиге; 3) теоремы Кастилиано; 4) обобщенного закона Гука. Решение: 1) Ответ неверный! В соответствии с принципом Сен-Венана распределение напряжений существенно зависит от способа приложения внешних сил только вблизи места их приложения, а в сечениях, достаточно удаленных от места приложения сил, распределение напряжений зависит только от статического эквивалента этих сил. 2) Ответ неверный! Закон Гука при деформации чистый сдвиг устанавливает линейную зависимость между касательными напряжениями и угловой деформацией, т.е. 3) Ответ неверный! Теорема Кастилиано доказывает, что частная производная от потенциальной энергии системы по силе равна перемещению точки приложения силы по направлению этой силы. 4) Ответ верный. Напряженное и деформированное состояния в точке тела связаны друг с другом через свойства материала. В пределах малых упругих деформаций эта зависимость является линейной и носит название обобщенного закона Гука. Наиболее простую форму этот закон принимает для изотропного материала. Задача 4.4.2: Совокупность линейных и угловых деформаций, возникающих по различным осям и в различных плоскостях, проходящих через данную точку тела, называют… 1) депланацией; 2) перемещением точки; 3) деформированным состоянием в точке; 4) объемной деформацией. Решение: 1) Ответ неверный! Депланация – искажение плоской формы поперечного сечения стержня при его нагружении внешними силами. 2) Ответ неверный! Вектор, имеющий начало в точке недеформированного тела, а конец в этой же точке деформированного тела, называют полным перемещением точки. 3) Ответ верный.
В общем случае элементарный объем испытывает три линейные деформации и три угловые. Деформированное состояние в точке полностью определяется, если заданы шесть компонентов тензора деформаций (
4) Ответ неверный! Объемная деформация, или относительное изменение объема, – это отношение абсолютного изменения объема к первоначальному. Определяется по формуле Задача 4.4.3: Три взаимно перпендикулярные оси, в системе которых отсутствуют угловые деформации, называют… 1) главными осями деформированного состояния; 2) главными осями; 3) центральными осями; 4) осями симметрии. Решение: 1) Ответ верный. Среди множества осей, проходящих через точку, в которой исследуется деформированное состояние, существуют три взаимно перпендикулярные оси, в системе которых угловые деформации равны нулю. Эти оси называются главными осями деформированного состояния, а линейные деформации в этой системе – главными деформациями. 2) Ответ неверный! Оси, относительно которых центробежный момент инерции сечения равен нулю, а осевые моменты инерции принимают экстремальные значения, называют главными осями. 3) Ответ неверный! Центральными называют оси, которые проходят через центр тяжести поперечного сечения. 4) Ответ неверный! Линия, которая делит плоское сечение на две одинаковые фигуры, называется осью симметрии. Задача 4.4.4: Модуль упругости материала Е и коэффициент Пуассона μ заданы. Относительное изменение объема равно …
1) Решение: 1) Ответ неверный! Не учтены знаки «минус» при напряжениях 2) Ответ верный. Для определения относительного изменения объема используем формулу
3) Ответ неверный! Не учтено влияние одного из напряжений: 4) Ответ неверный! Относительное изменение объема – величина безразмерная.
Задача 4.4.5: На рисунке показано напряженное состояние в точке изотропного тела. Модуль упругости материала
1) Решение: 1) Ответ неверный! При подстановке значений напряжений в уравнение обобщенного закона Гука изменены обозначения осей. 2) Ответ неверный! Допущена ошибка в знаке для нормального напряжения
3) Ответ верный. Воспользуемся уравнением обобщенного закона Гука 4) Ответ неверный! При решении необходимо учесть, что Задача 4.4.6: Объемный элемент находится под действием нормальных напряжений, показанных на рисунке:
1) Решение: 1) Ответ верный. На основании обобщенного закона Гука, составим выражение для определения линейной деформации в направлении оси z: 2) Ответ неверный! При подстановке значений нормальных напряжений в уравнение обобщенного закона Гука не учтено влияние эффекта Пуассона (в формуле пропущен коэффициент Пуассона). 3) Ответ неверный! Допущена ошибка при алгебраических преобразованиях. 4) Ответ неверный! При вычислении сделана арифметическая ошибка.
|
||||||
|
Последнее изменение этой страницы: 2016-12-10; просмотров: 1148; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.117.184.125 (0.01 с.) |

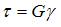 ,
,
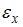 ,
, 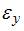 ,
, 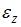 ,
, 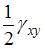 ,
, 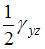 ,
, 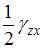 ). Зная эти компоненты, можно определить линейную и угловую деформации в любом направлении и в любой плоскости, проходящей через данную точку. Совокупность этих деформаций по множеству направлений и плоскостей, проходящих через данную точку, и называется деформированным состоянием в этой точке.
). Зная эти компоненты, можно определить линейную и угловую деформации в любом направлении и в любой плоскости, проходящей через данную точку. Совокупность этих деформаций по множеству направлений и плоскостей, проходящих через данную точку, и называется деформированным состоянием в этой точке.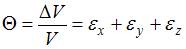 , где
, где 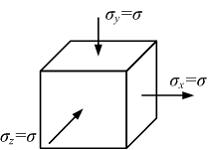
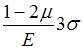 ; 2)
; 2) 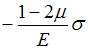 ; 3) 0; 4)
; 3) 0; 4) 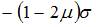
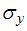 и
и 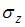 .
.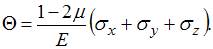
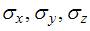 их значения, тогда
их значения, тогда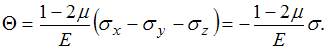
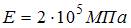 , коэффициент Пуассона
, коэффициент Пуассона 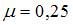 . Линейная деформация в направлении оси х равна…
. Линейная деформация в направлении оси х равна…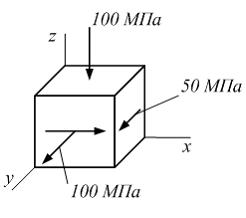
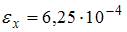 ; 2)
; 2) 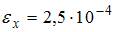 ; 3)
; 3) 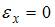 ; 4)
; 4) 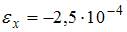 .
.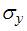 .
.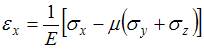 . В данном примере
. В данном примере 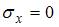 ,
, 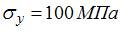 ,
, 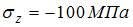 . После вычислений найдем
. После вычислений найдем 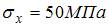 ,
, 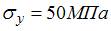 ,
, 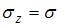 . Модуль упругости материала
. Модуль упругости материала  принимает значение…
принимает значение…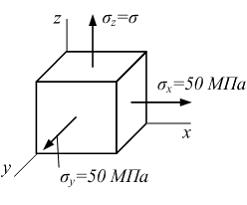
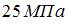 ; 2)
; 2) 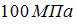 ; 3)
; 3) 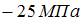 ; 4)
; 4) 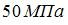 .
.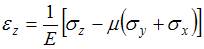 . Подставим в формулу числовые значения
. Подставим в формулу числовые значения 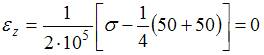 , тогда
, тогда 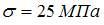 .
.


