
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Твердостью; 2) однородностью; 3) упругостью; 4) изотропностью.Содержание книги
Поиск на нашем сайте Введение в курс 1.1. Основные понятия, определения, допущения и принципы
Задача 1.1.1: Утверждение, что напряжения и перемещения в сечениях, удаленных от места приложения внешних сил, не зависят от способа приложения нагрузки, называется… Варианты ответов: 1) принципом независимости действия сил; 2) гипотезой плоских сечений; 3) принципом начальных размеров; 4) принципом Сен-Венана. Решение: 1) Ответ неверный! Принцип независимости действия сил предполагает, что результат от действия на тело системы сил равен сумме результатов от действия каждой силы в отдельности. 2) Ответ неверный! В соответствии с гипотезой плоских сечений (гипотеза Я. Бернулли) при растяжении стержня поперечные сечения, плоские и перпендикулярные к продольной оси до нагружения, остаются плоскими и перпендикулярными к оси стержня и после нагружения внешними силами. 3) Ответ неверный! Принцип начальных размеров вводит упрощение в методику расчета систем. Согласно этому принципу при составлении уравнений равновесия тело рассматривают как недеформированное, имеющее те же геометрические размеры, какие оно имело до нагружения внешними силами. 4) Ответ верный. Нагрузим стержень прямоугольного поперечного сечения, изготовленного из резины, силами F, приложенными в центре тяжести сечения. На поверхность стержня предварительно нанесена равномерная сетка из вертикальных линий. Стержень будет деформироваться, как показано на рисунке. Задача 1.1.2: Сопротивление материалов – это наука о методах расчета элементов инженерных конструкций на… Варианты ответов: 1) жесткость; 2) прочность; 3) устойчивость; 4) прочность, жесткость и устойчивость. Решение: 1) Ответ неверный! Кроме вопросов жесткости, в курсе «Сопротивлении материалов» рассматриваются вопросы прочности и устойчивости элементов инженерных конструкций. 2) Ответ неверный! Каждый элемент конструкции и конструкция в целом должны быть не только прочными, но и достаточно жесткими. Кроме этого, форма конструкции не должна существенно изменяться при действии на нее внешних сил (это свойство называется устойчивостью конструкции). Поэтому наука «Сопротивление материалов» занимается не только вопросами прочности, но и в равной степени вопросами жесткости и устойчивости элементов конструкций. 3) Ответ неверный! Кроме вопросов устойчивости, в курсе «Сопротивлении материалов» рассматриваются вопросы прочности и жесткости элементов инженерных конструкций. 5) Ответ верный. В процессе эксплуатации материал инженерных конструкций не должен разрушаться; перемещения отдельных точек конструкции не должны превосходить определенных, наперед заданных величин; форма конструкции не должна существенно изменяться. Если эти требования не выполняются, конструкция перестает нормально функционировать. Методы сопротивления материалов позволяют рассчитывать элементы инженерных конструкций так, чтобы они были прочными, достаточно жесткими, а их состояние устойчивым. Задача 1.1.3: Способность конструкции, элементов конструкции сопротивляться внешним нагрузкам в отношении изменения формы и размеров называется… Варианты ответов: 1) упругостью; 2) устойчивостью; 3) твердостью; 4) жесткостью. Решение: 1) Ответ неверный! Упругость – свойство материала тела восстанавливать свои первоначальные размеры после снятия внешних сил. 2) Ответ неверный! Устойчивость – свойство системы сохранять свое состояние при внешних воздействиях. 3) Ответ неверный! Твердость – свойство материала тела сопротивляться проникновению в него другого, более твердого тела. Ответ верный. Твердые тела в той или иной мере способны до определенного предела воспринимать воздействие внешних сил без разрушения и без существенного изменения первоначальных геометрических размеров. Способность тела сопротивляться внешним нагрузкам в отношении изменения формы и размеров называется жесткостью. Задача 1.1.4: Свойство материала тела восстанавливать свои первоначальные размеры после снятия внешних сил называется… Варианты ответов: Ответ верный. Под действием внешних сил реальное тело меняет геометрические размеры. После снятия внешних сил размеры тела полностью или частично восстанавливаются. Свойство материала тела восстанавливать свои первоначальные размеры называется упругостью. 4) Ответ неверный! Сплошная среда принимается изотропной, если свойства любого тела, выделенного из сплошной среды, не зависят от его исходной угловой ориентации. Задача 1.1.5: В соответствии с принципом независимости действия сил (принцип суперпозиции) … 1) механические характеристики материала в окрестности заданной точки не зависят от угловой ориентации выделенного из тела образца; 2) результат действия системы сил равен сумме результатов действий каждой силы в отдельности; 3) при снятии нагрузки форма и размеры тела полностью восстанавливаются; 4) большинство расчетов в сопротивлении материалов производится по недеформированной схеме. Решение: 1) Ответ неверный! Материал, обладающий таким свойством, называется изотропным материалом и данное положение является допущением об изотропности материала. Если механические характеристики материала зависят от угловой ориентации выделенного из тела образца, то такой материал называется анизотропным. 2) Ответ верный. В соответствии с принципом независимости действия сил результат действия системы сил равен сумме результатов действий каждой силы в отдельности. Рассмотрим пример. Один и то же упругий стержень нагружается системой сил 3) Ответ неверный! Данное положение является допущением об абсолютной упругости материала тела. Оно используется при решении большинства задач сопротивления материалов. 4) Ответ неверный! Данное положение называется принципом начальных размеров или принципом отвердения. Под воздействием внешних сил конструкция деформируется. Перемещения отдельных точек конструкции при этом настолько малы, что результаты расчетов по недеформированной и деформированной схемам практически совпадают.
Задача 1.1.6: Механическое свойство, характеризующее способность материала сопротивляться его разрушению под действием внешних сил, называется… 1) твердостью; 2) упругостью; 3) изотропностью; 4) прочностью. Решение: 1) Ответ неверный! Твердость – способность материала сопротивляться проникновению в него другого, более твердого тела. 2) Ответ неверный! Упругость – свойство материала тела восстанавливать свои первоначальные размеры после снятия внешних сил. 3) Ответ неверный! Изотропным называют материал, у которого механические свойства во всех направлениях одинаковы. 4) Ответ верный. Элементы конструкции должны проектироваться и создаваться таким образом, чтобы они были прочными, т.е. могли воспринимать все силовые воздействия, не разрушаясь в течение времени эксплуатации конструкции. Механическое свойство материала, характеризующее его способность сопротивляться разрушению под действием внешних сил, называется прочностью. Перемещения и деформация
Задача 1.4.1: Упрощение, на основании которого при составлении уравнений равновесия тело, после нагружения внешними силами рассматривают как недеформированное, называется… Варианты ответов: 1) принципом независимости действия сил; 2) принципом начальных размеров; 3) условием неразрывности деформаций; 4) твердостью. Решение: 1) Ответ неверный! Принцип независимости действия сил состоит в следующем. Если к системе приложено несколько сил, то можно определить внутренние силы, напряжения, перемещения, деформации от каждой силы отдельно, а результат одновременного действия всех сил получить как сумму результатов действий каждой силы в отдельности. 2) Ответ верный. Все твердые тела под действием внешних сил деформируются, то есть меняют свои размеры. Для подавляющего большинства тел перемещения точек являются малыми по сравнению с геометрическими размерами тела. На основании малости перемещений в методику анализа внутренних сил в теле вводят упрощение. При составлении уравнений равновесия тело рассматривают как недеформированное, имеющее те же геометрические размеры, какие оно имело до нагружения внешними силами. Это упрощение носит название «принцип начальных размеров». 3) Ответ неверный! При определении внутренних сил в произвольном сечении тела его мысленно рассекают на две части в этом сечении. Внутренние силы должны быть распределены по сечению так, чтобы деформированные поверхности сечения при совмещении двух частей тела полностью совпали. Такое условие носит название условия неразрывности деформаций. 4) Ответ неверный! Твердость – способность материала противодействовать механическому проникновению в него другого, более твердого тела.
Задача 1.4.2: Первоначальная длина стержня равна l. После приложения растягивающей силы длина стержня стала l 1. Величина
Варианты ответов: 1) абсолютным удлинением; 2) абсолютным укорочением в направлении оси x; 3) средним удлинением; 4) напряжением. Решение: 1) Ответ верный. Первоначальная длина стержня равна l. После приложения растягивающей силы длина стержня стала l 1. Величина 2) Ответ неверный! В данном случае не может быть абсолютного укорочения в направлении оси x, так как на стержень действует растягивающая сила. 3) Ответ неверный! Средним удлинением на отрезке длиной s называется отношение приращения длины отрезка 4) Ответ неверный! Напряжение связано с усилиями, действующими в сечении. В данном случае мы имеем вопрос об изменении длины стержня. Задача 1.4.3: Угловым перемещением сечения (см. рис.) является величина…
Варианты ответов: 1) Решение: 1) Ответ неверный! Величина 2) Ответ верный. При плоском изгибе поперечное сечение стержня, в общем случае, имеет два перемещения: линейное (прогиб 3) Ответ неверный. Величина F является нагрузкой, действующей на стержень. 4) Ответ неверный! Величина L – длина балки, а не угловое перемещение. Задача 1.4.4: Количественная мера изменения геометрических размеров в окрестности точки называется… Варианты ответов: 1) полным перемещением точки; 2) абсолютным удлинением стержня; 3) линейной деформацией; 4) деформированным состоянием в точке. Решение: 1) Ответ неверный! Вектор, имеющий начало в точке недеформированного тела, а конец в той же точке деформированного тела, называется вектором полного перемещения точки. 2) Ответ неверный! Величина, которая представляет разность между конечной длиной стержня после его нагружения внешними силами и начальной длиной, называется абсолютным удлинением стержня. 3) Ответ верный. Рассмотрим точки В и С в недеформированном теле, которое расположены на расстоянии S друг от друга. После нагружения тела внешними силами они займут новое положение 4) Ответ неверный! Совокупность линейных и угловых деформаций по различным направлениям и плоскостям для одной точки называется деформированным состоянием в точке. Задача 1.4.5: В результате действия внешних сил на деформируемое тело точка К заняла новое положение К1. Вектор 1) полным перемещением; 2) угловой деформацией; 3) проекцией вектора перемещения; 4) линейной деформацией. Решение: 1) Ответ верный.
В результате действия внешних сил на деформируемое тело точка К заняла новое положение К1. Вектор
2) Ответ неверный! Угловая деформация связана с изменением угла. 3) Ответ неверный! В задании задано перемещение точки, а не его проекция. 4) Ответ неверный! Линейная деформация является относительной величиной.
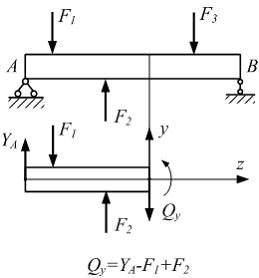
Растяжение и сжатие Сдвиг. Кручение Плоский прямой изгиб 6.1. Поперечная сила, изгибающий момент и их эпюры Задача 6.1.1: Поперечная сила Qy в произвольном поперечном сечении стержня численно равна алгебраической сумме проекций на ось… 1) y всех внешних сил, расположенных по одну сторону от рассматриваемого сечения; 2) x всех внешних сил, действующих по одну сторону от рассматриваемого сечения; 3) y всех внешних сил, действующих на стержень; 4) y всех внешних и внутренних сил, действующих на стержень. Решение: 1) Ответ верный. Поперечная сила Qy в произвольном поперечном сечении стержня численно равна алгебраической сумме проекций на ось y всех внешних сил (в том числе и реакций внешних связей), расположенных по одну сторону от рассматриваемого сечения.
2) Ответ неверный! Допущена ошибка в понимании терминов «поперечная сила» и «продольная сила». Продольная сила N в произвольном поперечном сечении стержня равна алгебраической сумме проекций на ось x стержня всех внешних сил, расположенных по одну сторону от рассматриваемого сечения. Поперечная сила Qy равна алгебраической сумме проекций на ось y всех внешних сил, расположенных по одну сторону от рассматриваемого сечения. 3) Ответ неверный! Допущена ошибка в применении метода сечений. Метод сечений заключается в следующем. В пределах рассматриваемого участка, проводят сечение, перпендикулярное к оси стержня. Одну часть стержня отбрасывают. Действие отброшенной части на оставшуюся заменяют внутренними силовыми факторами, одним из которых является поперечная сила. Поперечную силу прикладывают таким образом, чтобы она вращала рассматриваемую часть относительной внутренней точки этой части по часовой стрелке. В этом случае поперечная сила считается положительной. Затем составляют уравнение равновесия для оставленной части. Следовательно, поперечная сила равна алгебраической сумме проекций на ось y всех внешних сил, приложенных по одну сторону от рассматриваемого сечения. 4) Ответ неверный! Допущена ошибка в применении метода сечений. Внутренние силы, или силы взаимодействия между частицами тела, всегда входят попарно, отличаясь друг от друга знаками. Поэтому геометрическая сумма всех внутренних сил в теле равна нулю. Следовательно, алгебраические суммы проекций внутренних сил на какую-либо ось также равны нулю. Задача 6.1.2: Балка нагружена равномерно распределенной нагрузкой интенсивности q. Эпюра изгибающих моментов имеет вид…
1) 3) Решение: 1), 2) Ответ неверный! Допущена ошибка в построении эпюры изгибающих моментов. При данном виде нагружения балки эпюра изгибающих моментов будет изменяться по закону квадратной параболы. 3) Ответ верный. При данном виде нагружения эпюра изгибающих моментов изменяется по закону квадратной параболы. В середине эпюры будет максимум. Эпюра в зависимости от того, на сжатом или растянутом слое балки она строится, будет иметь вид показанный на рисунке 3). 4) Ответ неверный! Допущена ошибка в построении эпюры изгибающих моментов. Построена эпюра для случая нагружения балки в середине пролета сосредоточенной силой. Задача 6.1.3: Эпюра изгибающих моментов имеет вид…
1) 3) Решение: 1) Ответ неверный! Допущена ошибка в построении эпюры изгибающих моментов. Такой вид эпюра имеет для случая нагружения балки равномерно распределенной нагрузкой. 2), 3) Ответ неверный! Допущена ошибка в построении эпюры изгибающих моментов. На рисунке представлена эпюра поперечных сил. 4) Ответ верный. При данном виде нагружения в пределах каждого участка эпюра изгибающих моментов изменяется по линейному закону. В точке приложения сосредоточенной силы должно быть изменение угла наклона эпюры (излом). Эпюра будет иметь вид, представленный на рисунке 4) в зависимости от того, на сжатом или растянутом слое она построена. Задача 6.1.4: Балка нагружена распределенной нагрузкой, меняющейся по закону
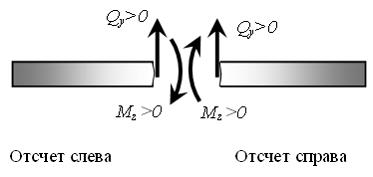
1) синуса; 2) косинуса; 3) прямой, параллельной оси балки; 4) прямой, наклонной к оси балки. Решение: 1) Ответ неверный! Допущена ошибка при использовании дифференциальных зависимостей при поперечном изгибе. Необходимо вспомнить, что интеграл от синуса будет равен минус косинус. 2) Ответ верный. Воспользуемся дифференциальными зависимостями при плоском поперечном изгибе 3) Ответ неверный! Поперечная сила изменяется по закону прямой, параллельной оси балки, в случае, когда на участке нет распределенной нагрузки. 4) Ответ неверный! Из дифференциальных зависимостей при плоском поперечном изгибе известно, что поперечная сила меняется по линейному закону тогда, когда на участке балки действует равномерно распределенная нагрузка. Задача 6.1.5: Правило знаков для поперечной силы Qy и изгибающего момента Мz изображено на рисунке… 1) 2) 3) 4) Решение: 1), 4) Ответ неверный! Не выполняется закон о равенстве действия и противодействия. Допущена ошибка в правиле знаков при применении метода сечений. Поперечную силу прикладывают таким образом, чтобы она вращала рассматриваемую часть по часовой стрелке. Она считается положительной, если вектор образует правую систему координат с вектором внешней нормали к сечению. Изгибающий момент считают положительным, если сжатый слой находится сверху (вогнутость балки направлена вверх). 2) Ответ неверный! Допущена ошибка в понимании терминов «поперечная сила» и «продольная сила». Продольная сила N в произвольном поперечном сечении стержня равна алгебраической сумме проекций на продольную ось стержня всех внешних сил, приложенных по одну сторону от рассматриваемого сечения. Поперечная сила Qy равна алгебраической сумме проекций на поперечную ось y всех внешних сил, приложенных по одну сторону от рассматриваемого сечения. Для изгибающих моментов не выполняется закон о равенстве действия и противодействия. Изгибающий момент считают положительным, если сжатый слой находится сверху (вогнутость балки направлена вверх). 3) Ответ верный. Поперечную силу прикладывают таким образом, чтобы она вращала рассматриваемую часть по часовой стрелке. Поперечная сила считается положительной, если вектор образует правую систему координат с вектором внешней нормали к сечению. Изгибающий момент считают положительным, если сжатый слой находится сверху (вогнутость балки направлена вверх). Кроме того, должен выполняться закон о равенстве действия и противодействия.
Задача 6.1.6: Пусть ось z направлена вдоль оси стержня. Оси x и y – главные центральные оси поперечного сечения. Для распределенной нагрузки q, поперечной силы Qy и изгибающего момента Mx выполняется(-ются) следующая(-ие) зависимость(-ти)… 1) 3) Решение: 1) Ответ верный. Между указанными величинами существуют дифференциальные зависимости 2) Ответ неверный! Допущена ошибка в нахождении производной. Производные берутся не по времени, а по координате z, направленной вдоль оси стержня. 3), 4) Ответ неверный! Допущена ошибка в определении зависимостей между q, Qy и Mx. Поперечная сила представляет собой производную от изгибающего момента по координате z, а производная по z от поперечной силы дает интенсивность внешней распределенной нагрузки. 6.2. Напряжения в поперечном сечении стержня при плоском изгибе Задача 6.2.1: При плоском поперечном изгибе нормальные напряжения по ширине сечения балки … 1) распределяются по закону квадратной параболы; максимальное значение принимают посередине, а по краям равны нулю; 2) распределяются равномерно; 3) равны нулю; 4) распределяются по линейному закону; максимальны по краям; равны нулю посередине. Решение: 1) Ответ неверный! Указано распределение касательных напряжений по высоте балки при изгибе. По ширине сечения балки нормальные напряжения при изгибе распределяются равномерно. 2) Ответ верный. По ширине сечения балки нормальные напряжения при изгибе распределяются равномерно. 3) Ответ неверный! По ширине сечения балки нормальные напряжения при изгибе распределяются равномерно. 4) Ответ неверный! Указано распределение нормальных напряжений по высоте балки при изгибе. По ширине сечения балки нормальные напряжения при изгибе распределяются равномерно.
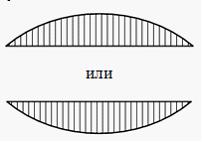
Задача 6.2.2: При плоском изгибе стержня нормальные напряжения по высоте поперечного сечения… 1) изменяются по закону квадратной параболы; в самых верхних и нижних точках поперечного сечения равны нулю и достигают максимума на нейтральной линии; 2) не изменяются; 3) имеют линейный закон распределения; равны нулю на нейтральной линии и достигают максимума в точках, наиболее удаленных от нее; 4) имеют линейный закон распределения; достигают максимума на нейтральной линии и равны нулю в точках, наиболее удаленных от нее. Решение: 1) Ответ неверный! Здесь описано распределение касательных напряжений по высоте балки прямоугольного сечения. Нормальные же напряжения при изгибе имеют линейный закон распределения по высоте поперечного сечения 2), 4) Ответ неверный! Допущена ошибка в применении формулы 3) Ответ верный. Нормальные напряжения при плоском изгибе по высоте поперечного сечения стержня имеют линейный закон распределения Задача 6.2.3: Вывод формулы для определения нормальных напряжений при чистом изгибе основывается на… 1) законе парности касательных напряжений и теореме Кастильяно; 2) гипотезе наибольших касательных напряжений и гипотезе об удельной потенциальной энергии формоизменения; 3) гипотезе наибольших нормальных напряжений и гипотезе наибольших линейных деформаций; 4) гипотезе плоских сечений и гипотезе об отсутствии взаимного надавливания продольных слоев балки. Решение: 1) Ответ неверный! Закон парности касательных напряжений и теорема Кастильяно не используются при выводе формулы для определения нормальных напряжений при чистом изгибе. 2) Ответ неверный! Эти гипотезы являются гипотезами прочности (пластичности), т.е. гипотезами причины разрушения материала или возникновения в нем состоянии текучести. Гипотезы прочности позволяют оценить прочность материала при любом напряженном состоянии, если из опыта известна его прочность при растяжении. 3) Ответ неверный! Эти гипотезы являются гипотезами прочности (разрушения), т.е. гипотезами причины разрушения материала или возникновения в нем состоянии текучести. Гипотезы прочности позволяют оценить прочность материала при любом напряженном состоянии, если из опыта известна его прочность при растяжении. 4) Ответ верный. Вывод формулы для определения нормальных напряжений при чистом изгибе основывается на гипотезе плоских сечений и гипотезе отсутствия взаимного надавливания продольных слоев балки. Задача 6.2.4: Прямоугольная балка имеет два варианта расположения поперечного сечения. Отношение наибольших нормальных напряжений
1) 2; 2) 1,5; 3) 1; 4) 0,5. Решение: 1) Ответ верный. Наибольшие напряжения в указанных случаях определяются следующим образом: 2), 3) Ответ неверный! Нормальные напряжения распределяются по высоте сечения согласно формуле 4) Ответ неверный! Допущена ошибка в нахождении момента сопротивления изгибу. Момент сопротивления изгибу прямоугольного сечения находится по формуле
Задача 6.2.5: Направление касательных напряжений, передающихся через ступенчатый разрез от правой части балки на левую, показано на рисунке…
1) 3) Решение: 1) Ответ неверный! Допущена ошибка в определении направления поперечной силы. В данном сечении поперечная сила 2) Ответ верный.
3), 4) Ответ неверный! Допущена ошибка в определении направления касательных напряжений на площадке bc. На площадке bc направление касательных напряжений подчиняется закону парности.
Задача 6.2.6: Схема нагружения балки прямоугольного сечения с размерами
1) Решение: 1) Ответ неверный! Допущена ошибка при вычислении изгибающего момента в сечении 2) Ответ верный. Воспользуемся формулой для определения нормальных напряжений при плоском поперечном изгибе: 3) Ответ неверный! Допущена ошибка при вычислении осевого момента инерции сечения. 4) Ответ неверный! Допущена ошибка при определении значения y.
6.3. Расчет балок на прочность Задача 6.3.1: Из таблицы сортаментов для двутавровых балок имеем: 1) 0,985; 2) 4,92; 3) 3,34; 4) 3,1. Решение: 1) Ответ неверный! Допущена ошибка в использовании отношения моментов сопротивления изгибу. Отношение масс подобранных профилей равно отношению площадей поперечных сечений. Балка прямоугольного сечения тяжелее балки двутаврового сечения в 3,1 раза. 2) Ответ неверный!
3) Ответ неверный! Допущена ошибка в определении профиля двутавровой балки. По условию прочности необходимо брать двутавр с моментом сопротивления изгибу большим, чем расчетный (№ 20а). В данном случае взят двутавр с меньшим моментом сопротивления (№ 20). 4) Ответ верный. Составим условие прочности при изгибе балки |
|
| Поделиться: |


 ,
,  , а затем поочередно силами
, а затем поочередно силами 


 – результат действия системы сил
– результат действия системы сил  – результат действия силы
– результат действия силы  – результат действия силы
– результат действия силы  . Принцип независимости действия сил применим для большинства задач, решаемых в курсе сопротивление материалов. Он позволяет сложную задачу разделить на ряд простых, решить их по отдельности, а результаты решений сложить и таким образом получить решение исходной сложной задачи.
. Принцип независимости действия сил применим для большинства задач, решаемых в курсе сопротивление материалов. Он позволяет сложную задачу разделить на ряд простых, решить их по отдельности, а результаты решений сложить и таким образом получить решение исходной сложной задачи. называется…
называется…
 называется абсолютным удлинением
называется абсолютным удлинением к его начальной длине
к его начальной длине .
.
 ; 2)
; 2) 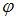 ; 3) F; 4) L.
; 3) F; 4) L. и
и  , а расстояние между ними изменится на величину
, а расстояние между ними изменится на величину 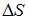 . Отношение приращения длины отрезка
. Отношение приращения длины отрезка  .
.
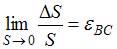 .
. является количественной мерой изменения геометрических размеров в окрестности точки В по направлению ВС и называется линейной деформацией.
является количественной мерой изменения геометрических размеров в окрестности точки В по направлению ВС и называется линейной деформацией. называется…
называется…

 ; 2)
; 2)  ;
; ; 4)
; 4)  .
.
 ; 2)
; 2)  ; 4)
; 4)  .
. . Поперечная сила по длине балки изменяется по закону …
. Поперечная сила по длине балки изменяется по закону …

 и q,составимвыражение для определения поперечной силы
и q,составимвыражение для определения поперечной силы  , или
, или
 ;
; ;
; ;
; .
. ; 2)
; 2)  ;
; ; 4)
; 4)  .
. .
.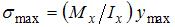 , и равны нулю на нейтральной линии.
, и равны нулю на нейтральной линии. для этих двух вариантов равно…
для этих двух вариантов равно…
 ,
, 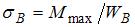 , где моменты сопротивления изгибу равны
, где моменты сопротивления изгибу равны  ,
,  . Следовательно, искомое отношение:
. Следовательно, искомое отношение:  .
. . Тогда наибольшие напряжения равны
. Тогда наибольшие напряжения равны  .
. , где В – ширина сечения, Н – его высота.
, где В – ширина сечения, Н – его высота.
 ; 2)
; 2) 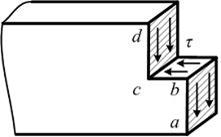 ;
; ; 4)
; 4)  .
.
 представлена на рисунке. Сила F и размер l заданы. Значение нормального напряжения в точке «К» сечения
представлена на рисунке. Сила F и размер l заданы. Значение нормального напряжения в точке «К» сечения  равно…
равно…
 ; 2)
; 2)  ; 3)
; 3)  ; 4)
; 4)  .
. .
.
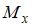 − изгибающий момент в сечении балки, в котором определяются нормальные напряжения;
− изгибающий момент в сечении балки, в котором определяются нормальные напряжения;  − осевой момент инерции сечения относительно главной центральной оси, перпендикулярной плоскости действия изгибающего момента;
− осевой момент инерции сечения относительно главной центральной оси, перпендикулярной плоскости действия изгибающего момента;  − расстояние от главной центральной оси до точки, в которой определяется нормальное напряжение.
− расстояние от главной центральной оси до точки, в которой определяется нормальное напряжение. Осевой момент инерции прямоугольного сечения относительно главной центральной оси найдем по формуле
Осевой момент инерции прямоугольного сечения относительно главной центральной оси найдем по формуле  При заданных значениях b и h получим
При заданных значениях b и h получим  Расстояние у от главной центральной оси до точки «К» равно b. Следовательно,
Расстояние у от главной центральной оси до точки «К» равно b. Следовательно, 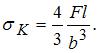


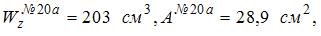

 . Отношение массы балки прямоугольного сечения (с отношением сторон
. Отношение массы балки прямоугольного сечения (с отношением сторон 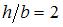 ) к массе балки двутаврого сечения равно….
) к массе балки двутаврого сечения равно….
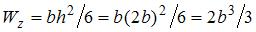 ;
; .
. . Момент сопротивления
. Момент сопротивления 


