
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Расчет на прочность при крученииСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Задача 3.3.1: Стержень круглого поперечного сечения диаметром d работает на деформацию кручение. Касательное напряжение в точке, которая расположена на расстоянии Варианты ответов: 1) Решение: 1) Ответ неверный! Касательные напряжения в поперечном сечении круглого стержня меняются вдоль радиуса по линейному закону, а не являются постоянными. 2) Ответ верный. Эпюра распределения касательных напряжений в поперечном сечении круглого стержня имеет вид, показанный на рисунке. 3) Ответ неверный! При вычислении допущена ошибка в определении 4) Ответ неверный! Получен неверный результат из-за непонимания формулы для определения касательных напряжений при кручении стержня с круглым поперечным сечением.
Задача 3.3.2: Условие прочности при кручении стержня круглого поперечного сечения с неизменным по длине диаметром имеет вид… Варианты ответов: 1) Решение: 1), 3) Ответ неверный! При кручении в поперечных сечениях возникают касательные напряжения. 2) Ответ верный.
4) Ответ неверный! Максимальные касательные напряжения возникают в наиболее удаленных от центра точках.
Задача 3.3.3: Из условия прочности, при заданном значении
Варианты ответов: 1) Решение: 1) Ответ неверный! Возможна ошибка в записи выражения условия прочности. 2) Ответ неверный! Возможна ошибка при определении крутящих моментов в поперечных сечениях грузовых участков. 3) Ответ верный. Так как вал постоянного диаметра, условие прочности имеет вид 4) Ответ неверный! Возможна ошибка в вычислении полярного момента сопротивления поперечного сечения. Задача 3.3.4: При кручении максимальное касательное напряжение возникает в точке…
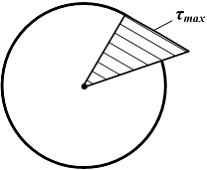
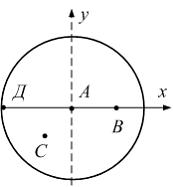
Варианты ответов: 1) В; 2) Д; 3) А; 4) С. Решение: 1) Ответ неверный! Точка В удалена от центра не на максимальное расстояние. 2) Ответ верный. Для определения максимального касательного напряжения используем выражение 3) Ответ неверный! Возможна ошибка при использовании формулы для максимальных касательных напряжений в определении расстояния 4) Ответ неверный! Точка С удалена от центра не на максимальное расстояние.
Задача 3.3.5: Ступенчатый стержень скручивается моментами М. Наибольшее касательное напряжение на участке диаметром d равно
Варианты ответов: 1) Решение: 1) Ответ неверный! Допущена арифметическая ошибка при определении полярного момента сопротивления. 2) Ответ неверный! Величина максимального касательного напряжения при кручении стержня с круглым поперечным сечением не уменьшается пропорционально расстоянию от оси стержня. 3) Ответ верный. При определении максимального касательного напряжения в поперечном сечении круглого стержня диаметром d воспользуемся формулой 4) Ответ неверный! При определении максимального касательного напряжения в поперечном сечении используется формула
Задача 3.3.6: Труба испытывает деформацию кручение. Касательное напряжение в точке С поперечного сечения трубы равно 1) 0,33; 2) 12; 3) 6; 4) 3. Решение: 1) Ответ неверный! Коэффициент запаса прочности определяется по формуле 2) Ответ неверный! При удалении от центра тяжести касательное напряжение увеличивается, и в точках у внешней поверхности трубы его значение равно 3) Ответ неверный! Максимальные касательные напряжения действуют в точках у внешней поверхности трубы и равны 4) Ответ верный. Максимальное касательное напряжение возникает в точках у внешней поверхности трубы и его значение в два раза больше напряжения в точке С. Поэтому коэффициент запаса прочности
|
||
|
Последнее изменение этой страницы: 2016-12-10; просмотров: 2604; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.214 (0.006 с.) |

 от оси стержня, равно
от оси стержня, равно  . Наибольшее касательное напряжение в данном поперечном сечении стержня равно…
. Наибольшее касательное напряжение в данном поперечном сечении стержня равно… ; 2)
; 2)  ; 3)
; 3)  ; 4)
; 4)  .
.
 .
.
 − крутящий момент в данном сечении;
− крутящий момент в данном сечении; − полярный момент инерции сечения;
− полярный момент инерции сечения;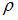 − расстояние от оси стержня до точки, в которой определяется касательное напряжение.
− расстояние от оси стержня до точки, в которой определяется касательное напряжение. имеем
имеем 


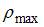 . Значение
. Значение 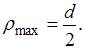
 ; 2)
; 2) 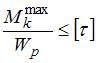 ; 3)
; 3)  ; 4)
; 4)  .
.
 , где
, где  ,
, 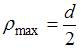 , d – диаметр стержня.
, d – диаметр стержня.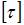 , наименьший допускаемый диаметр вала равен…
, наименьший допускаемый диаметр вала равен… .
.
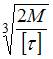 ; 2)
; 2) 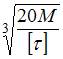 ; 3)
; 3) 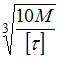 ; 4)
; 4)  .
. , где
, где  .
.
 ,
,  .
. . Значение наибольшего касательного напряжения на участке с диаметром 2 d равно…
. Значение наибольшего касательного напряжения на участке с диаметром 2 d равно…
 ; 2)
; 2)  ; 3)
; 3)  ; 4)
; 4)  .
.
 − полярный момент сопротивления, который определяется по формуле
− полярный момент сопротивления, который определяется по формуле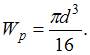
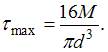


 . Предел текучести материала трубы при чистом сдвиге
. Предел текучести материала трубы при чистом сдвиге  . Коэффициент запаса прочности
. Коэффициент запаса прочности  равен …
равен … . В нашем случае
. В нашем случае  . Следовательно,
. Следовательно,  .
. , поэтому
, поэтому  .
.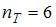 не верен.
не верен. .
.


