
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Валы и оси. Основы расчета на прочность, жесткость и выносливостьСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте При работе валы и вращающиеся оси даже при постоянной внешней нагрузке испытывают знакопеременные напряжения изгиба симметричного цикла, следовательно, возможно усталостное разрушение валов и вращающихся осей. Чрезмерная деформация валов может нарушить нормальную работу зубчатых колес и подшипников, следовательно, основными критериями работоспособности валов и осей являются сопротивление усталости материала и жесткость. Практика показывает, что разрушение валов быстроходных машин обычно происходит в результате усталости материала. Для окончательного расчета вала необходимо знать его конструкцию, тип и расположение опор, места приложения внешних нагрузок. Вместе с тем подбор подшипников можно осуществить только тогда, когда известен диаметр вала. Поэтому расчет валов выполняется в два этапа: предварительный (проектный) и окончательный (проверочный). Предварительный расчет валов. Проектный расчет производится только на кручение, причем для компенсации напряжений изгиба и других неучтенных факторов принимают значительно пониженные значения допускаемых напряжений кручения, например, для выходных участков валов редукторов [τк] = (0,025...0,03)σв, где σв – временное сопротивление материала вала. Тогда диаметр вала определится из условия прочности τк =Мк/(0,2 d 3) ≤ [τк], откуда:
Полученное значение диаметра округляется до ближайшего стандартного размера, согласно ГОСТ «Нормальные линейные размеры», устанавливающего четыре ряда основных и ряд дополнительных размеров; последние допускается применять лишь в обоснованных случаях. Так, из ряда Rа 40 указанного стандарта в диапазоне от 16 до 100мм предусмотрены следующие основные нормальные линейные размеры. 16,17, 18, 19, 20, 21, 22, 24, 25, 26, 28, 30, 32, 34, 36, 38, 40, 42, 45, 48, 50, 53, 56, 60, 63, 67, 71, 75, 80, 85, 90, 95, 100. Так как промышленность изготовляет подшипники качения с диаметром отверстия 35, 55, 65, 70мм в указанном диапазоне, то разрешается использовать для цапф валов и осей эти дополнительные размеры. При проектировании редукторов диаметр выходного конца ведущего вала можно принять равным диаметру вала электродвигателя, с которым вал редуктора будет соединен муфтой. После установления диаметра выходного конца вала назначается диаметр цапф вала (несколько больше диаметра выходного конца) и производится подбор подшипников. Диаметр посадочных поверхностей валов под ступицы насаживаемых деталей для удобства сборки принимают больше диаметров соседних участков. В результате этого ступенчатый вал по форме оказывается близок к брусу равного сопротивления. Расчетные схемы валов и осей (рис.2.13, а–д). При составлении расчетной схемы валы и оси рассматривают как балки, шарнирно закрепленные в жестких опорах, одна из которых подвижная. Нагрузки, передаваемые валам и осям со стороны насаженных на них деталей, полагают сосредоточенными и приложенными в середине ступицы (см. рис.2.13, д). Силы трения в подшипниках не учитывают, силами тяжести валов, осей и насаженных на них деталей обычно пренебрегают. Кроме того, в большинстве случаев пренебрегают усилиями, растягивающими или сжимающими вал.
Оси координат на расчетной схеме следует направлять вдоль векторов основных внешних сил. Если угол между плоскостями действия внешних сил не превышает 30°, то эти силы на расчетной схеме можно совмещать в одну плоскость. Радиальные реакции подшипников, а, следовательно, и условные опоры полагают расположенными следующим образом (рис.2.13): а – уподшипников скольжения на расстоянии 0,3...0,4 его длины от внутреннего торца, так как вследствие деформаций валов и осей давление по длине подшипника распределено неравномерно; б – у радиальных подшипников качения в середине их ширины; в, г – урадиально-упорных подшипников качения в точках О пересечения с осью вала нормали к площадке контакта в ее середине (размер а, определяющий расстояние точки О от клейменого торца подшипника, вычисляется по формулам в зависимости от размеров подшипника). На рис.2.14, а–е представлена расчетная схема ведущего вала цилиндрического редуктора с косозубыми колесами, нагруженного вращающим моментом Т,окружной силой Ft,радиальной силой Fr и осевой силой Fa. Здесь же представлены эпюры изгибающих моментов в вертикальной и горизонтальной плоскостях и эпюра крутящих моментов. Суммарный изгибающий момент в любом сечении вала определяется как геометрическая сумма изгибающих моментов в горизонтальной и вертикальной плоскостях по формуле
Одновременное действие изгибающего и крутящего моментов учитывается значением эквивалентного момента, например, по гипотезе наибольших касательных напряжений,
Окончательный расчет валов. Проверочный расчет валов выполняется на усталость и жесткость (расчеты на колебания мы рассматривать не будем). Упрощенный проверочный расчет валов на усталость исходит из предположения, что не только нормальные, но и касательные напряжения изменяются по симметричному (наиболее неблагоприятном) циклу. Этот вид расчета дает неточность на несколько процентов в сторону увеличения запаса прочности вала. Условие сопротивления усталости имеет вид σэкв = М экв/(0,1 d 3) < [σ–1и], где σэкв – эквивалентное напряжение в проверяемом сечении; М экв– эквивалентный момент; d– диаметр вала в этом сечении; [σ–1и] – допускаемое напряжение на изгиб при симметричном цикле изменения напряжений (табл. 2.6).
Таблица 2.6 Допускаемые напряжения на изгиб
Расчетный диаметр вала в проверяемом сечении определяется по формуле
и сравнивается с принятым при конструировании вала диаметром. Если проверяемое сечение вала ослаблено шпоночной канавкой, то расчетный диаметр вала следует увеличить на 7...10 %. Приведенные для проектного и проверочного расчета валов формулы и рекомендации используются и для расчета осей с учетом только нормальных напряжений изгиба, так как М к=0. Допускаемое напряжение [σи] для невращающихся и [σ–1и] – для вращающихся осей выбирают по табл. 2.6. Уточненный проверочный расчет валов на усталость исходит из предположения, что нормальные напряжения изменяются по симметричному, а касательные – по асимметричному циклу. Этот расчет заключается в определении фактического коэффициента запаса прочности в предположительно опасных сечениях с учетом характера изменения напряжений, влияния абсолютных размеров деталей, концентрации напряжений, шероховатости и упрочнения поверхностей. Условие сопротивления усталости имеет вид
где s σ, sτ– коэффициенты запаса прочности по нормальным и касательным напряжениям (их вычисление рассматривалось в сопротивлении материалов); [ s ] – допускаемый коэффициент запаса прочности; для валов передач [ s ] ≥ 1,3. В большинстве случаев можно ограничиться упрощенным проверочным расчетом валов. По известному эквивалентному напряжению в предположительно опасном сечении легко определить случаи, когда условия сопротивления усталости заведомо выполняются. Уточненный проверочный расчет на усталость производить нет необходимости, если σэкв ≤ σ–1и/(К [ s ]) ≈ σ, где σ–1и – предел выносливости гладкого образца при симметричном цикле нагружения; К – коэффициент снижения предела выносливости, определяемый по формуле К = (K σ/ Kd+ 1/ KF – 1)/ Кυ, где K σ– эффективный коэффициент концентрации напряжений; Kd – коэффициент влияния абсолютных размеров поперечного сечения; KF– коэффициент влияния шероховатости поверхности; Кυ – коэффициент влияния поверхностного упрочнения. Значения указанных коэффициентов приводятся в справочной литературе. На рис. 2.15 показаны основные концентраторы напряжений в валах и осях: а – галтель; б – выточка; в – поперечное отверстие; г – шпоночная канавка.
Рис. 2.15. Основные концентраторы напряжений в валах и осях Проверочный расчет на усталость ведется по номинальной длительно действующей нагрузке без учета кратковременных перегрузок (например, в период пуска или при динамических и ударных воздействиях), повторяемость которых невелика и не может вызвать усталостное разрушение. Расчет на статическую прочность. В случаях возможности возникновения кратковременныхпиковых нагрузок для предупрежденияостаточных деформацийпроводится проверочный расчет на статическую прочность по условию σэкв max= К П σэкв ≤ σт/[ s т], где К П – коэффициент перегрузки, равный отношению максимального момента двигателя к его номинальному значению (при наличии предохранительного устройства К Пзависит от момента, при котором срабатывает это устройство); σт – предел текучести материала; [sт] – допускаемый коэффициент запаса прочности по пределу текучести. Обычно принимают [ s t] = 1,2...1,8. Расчет валов и осей на жесткость. Под действием приложенных активных и реактивных сил валы изгибаются и скручиваются. Деформации валов при изгибе характеризуются прогибом у и углами поворота α поперечных сечений (рис. 2.16). Максимальный прогиб вала или оси называется стрелой прогиба и обозначается f. Деформация кручения вала характеризуется углом закручивания φ.
Рис. 2.16. Схема деформации валов при изгибе В результате прогиба и поворота сечений вала изменяется взаимное положение зубчатых венцов передач (рис.2.16) и элементов подшипников, что вызывает неравномерность распределения нагрузок по ширине венцов зубчатых колес и длине подшипников скольжения, перекос колец подшипников качения. Деформация кручения валов вызывает неравномерность распределения нагрузки по длине шлицев в шлицевых соединениях по длине венцов валов-шестерен, может быть причиной потери точности ходовых винтов токарно-винторезных станков и причиной возникновения крутильных колебаний валов. Деформация валов мало влияет на работу ременных и цепных передач, поэтому валы таких передач на жесткость не проверяют. Короткие валы, например, валы редукторов, на жесткость обычно не проверяют, так как прогибы и углы закручивания таких валов невелики, и жесткость их обеспечена. Условия жесткости валов записывают следующим образом: у ≤ [ у ]; f ≤ [ f ]; α ≤ [α]; Здесь [ у ] – допускаемый прогиб (в месте установки зубчатых колес, [ у ]≤ 0,01 m, где т – модуль зацепления); [ f ] – допускаемая стрела прогиба (для валов общего назначения в станкостроении [ f ] ≤ 0,0003 l, где l – длина пролета); [α] – допускаемый угол поворота сечения вала (для подшипников скольжения [α] = 0,001 рад, для подшипников качения [α] ≤ 0,05 рад и в значительной мере зависит от типа подшипника; для валов зубчатых передач для сечений в опорах [α] = 0,001 рад); Условие жесткости осей записывается так: f ≤ [ f ], здесь [ f ] ≤ 0,002 l, где l – расстояние между опорами.
|
|||||||||||||||
|
Последнее изменение этой страницы: 2016-08-16; просмотров: 1067; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.108 (0.012 с.) |






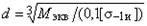



 .
. – допускаемый угол закручивания вала (
– допускаемый угол закручивания вала (


