Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Работа постоянной силы на прямолинейном перемещенииСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Определим работу для случая, когда действующая сила постоянна по величине и направлению, а точка ее приложения перемещается по прямолинейной траектории. Рассмотрим материальную точку С, к которой приложена постоянная по значению и направлению сила F.
За некоторый промежуток времени t точка С переместилась в положение С1 по прямолинейной траектории на расстояние s. Работа W постоянной силы F при прямолинейном движении точки ее приложения равна произведению модуля силы F на расстояние s и на косинус угла между направлением силы и направлением перемещения, т. е.
Угол? между направлением силы и направлением движения может меняться в пределах от 0 до 180°. При? < 90° работа положительна, при? > 90° — отрицательна, при? = 90° W = 0 (работа равна нулю). Еcли cила составляет с направлением движения острый угол, она называется движущей силой, ее работа всегда положительна. Если угол между направлениями силы и перемещения тупой, сила оказывает сопротивление движению, совершает отрицательную работу и носит название силы сопротивления. Примерами сил сопротивления могут служить силы резания, трения, сопротивления воздуха и другие, которые всегда направлены в сторону, противоположную движению. Когда? = 0, т. е. когда направление силы совпадает с направлением скорости, W = Fs, так как cos? = 1. Произведение F cos? есть проекция силы F на направление движения материальной точки. Следовательно, работу силы можно определить как произведение перемещения s и проекции силы F на направление движения точки. За единицу работы в Международной системе единиц (СИ) принят джоуль (Дж), равный работе силы в один ньютон (Н) на совпадающем с ней по направлению движения длиной в один метр (м):
Работа силы тяжести Гипермаркет знаний>>0%A4%D0%B8%D0%B7%D0%B8%D0%BA%D0%B0_%D0%B8_%D0%B0%D1%81%D1%82%D1%80%D0%BE%D0%BD%D0%BE%D0%BC%D0%B8%D1%8F"Физика и астрономия>>0%A4%D0%B8%D0%B7%D0%B8%D0%BA%D0%B0_10_%D0%BA%D0%BB%D0%B0%D1%81%D1%81"Физика 10 класс>>Физика: Работа силы тяжести
Вычислим работу, используя в этот раз не 0%92%D1%82%D0%BE%D1%80%D0%BE%D0%B9_%D0%B7%D0%B0%D0%BA%D0%BE%D0%BD_%D0%9D%D1%8C%D1%8E%D1%82%D0%BE%D0%BD%D0%B0"второй закон Ньютона, а явное выражение для сил взаимодействия между телами в зависимости от расстояний между ними. Это позволит нам ввести понятие потенциальной энергии - энергии, зависящей не от скоростей тел, а от расстояний между телами (или от расстояний между частями одного и того же тела).
Направления векторов силы тяжести
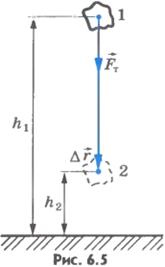
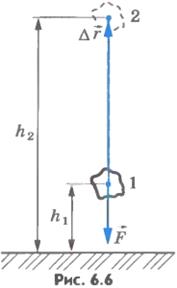
Пусть теперь тело бросили вертикально вверх из точки, расположенной на высоте h1, над поверхностью Земли, и оно достигло высоты h2 (рис.6.6).
Векторы
Если же тело перемещается по прямой так, что направление перемещения составляет угол
Из прямоугольного треугольника BCD видно, что
Формулы (6.12), (6.13), (6.14) дают возможность подметить важную закономерность. При прямолинейном движении тела работа силы тяжести в каждом случае равна разности двух значений величины, зависящей от положений тела в начальный и конечный моменты времени. Эти положения определяются высотами h1 и h2 тела над поверхностью Земли.
Таким образом, работа при перемещении вдоль кривой ВС равна:
При движении тела по замкнутой траектории работа силы тяжести равна нулю. В самом деле, пусть тело движется по замкнутому контуру ВСDМВ (рис.6.9). На участках ВС и DМ сила тяжести
Силы, обладающие такими свойствами, называют консервативными.
|
||
|
Последнее изменение этой страницы: 2016-08-16; просмотров: 3544; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.108 (0.005 с.) |



 . Применяется также более крупная единица работы — килоджоуль (кДж), 1 кДж = 1000 Дж = 10?Дж. В технической системе (МКГСС) за единицу работы принят килограмм-сила метр (кгс*м).
. Применяется также более крупная единица работы — килоджоуль (кДж), 1 кДж = 1000 Дж = 10?Дж. В технической системе (МКГСС) за единицу работы принят килограмм-сила метр (кгс*м).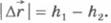 .
.
 и перемещения
и перемещения  совпадают. Согласно определению работы (см. формулу (6.2)) имеем
совпадают. Согласно определению работы (см. формулу (6.2)) имеем
 и
и 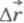 направлены в противоположные стороны, а модуль перемещения
направлены в противоположные стороны, а модуль перемещения  . Работу силы тяжести запишем так:
. Работу силы тяжести запишем так:
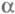 с направлением силы тяжести (рис.6.7), то работа силы тяжести равна:
с направлением силы тяжести (рис.6.7), то работа силы тяжести равна:
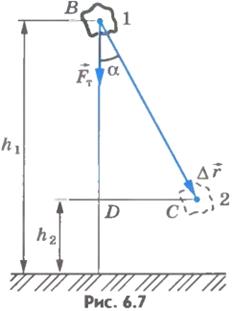
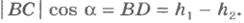 . Следовательно,
. Следовательно,


 совершает работы, равные по абсолютной величине, но противоположные по знаку. Сумма этих работ равна нулю. Следовательно, равна нулю и работа силы тяжести на всем замкнутом контуре.
совершает работы, равные по абсолютной величине, но противоположные по знаку. Сумма этих работ равна нулю. Следовательно, равна нулю и работа силы тяжести на всем замкнутом контуре.