Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Нормальные напряжения и их эпюрыСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте Определение нормальных напряжений и деформаций при косом изгибе основано на принципе независимости действия сил. Всю нагрузку проецируют на две главные плоскости балки и строят эпюры изгибающих моментов в этих двух плоскостях. Затем по известным формулам прямого изгиба определяют напряжения и деформации. [ 1 ] Для определения нормального напряжения в произвольной точке найдем его составляющие от каждого фактора для случая внецентренного растяжения. [ 2 ] Для определения нормальных напряжений по сечениям вдоль образующих аппарат рассматривают как балку, лежащую на принятом числе опор. Число опор выбирают в зависимости от материала аппарата, его длины и рабочих условий. Для наиболее распространенных размеров горизонтальных аппаратов и емкостей разработан стандарт на число опор и расстояние между ними. [ 3 ] Для определения нормальных напряжений ахх оказывается достаточно ввести гипотезу плоских сечений. [ 4 ] При определении нормальных напряжений и перемещений обычно учитывают только изгибающие моменты и пренебрегают влиянием перерезывающих сил. Это обусловлено двумя причинами: а) малым влиянием перерезывающих сил на величину нормальных напряжений и перемещений (особенно в тонких и длинных валах) и, главное, б) отсутствием инженерных методов расчета вала с учетом перерезывающих сил. [ 5 ] Формула для определения нормальных напряжений, возникающих в поперечных сечениях балок при прямом изгибе, а также выводы относительно положения нейтральной оси приводились к случаю, когда поперечное сечение балки имеет по меньшей мере одну ось симметрии и силовая плоскость проходит через эту ось. [ 6 ] Условия прочности при растяжении, сжатии. Допускаемые напряжения. Закон Гука при растяжении, сжатии. По определению относительная деформация стержня равна
где Если удлинение стержня
называется силовой деформацией (рис. 1.10, а). Если удлинение стержня вызвано изменением температуры
называется температурной деформацией (рис. 1.10, б).
Рис. 1.10. Силовая (а) и температурная (б) деформации В общем случае удлинение стержня происходит за счёт действия приложенных нагрузок и изменения температуры. Поэтому
и
Как показывает опыт, силовая деформация стержня (рис. 1.10, а) пропорциональна действующим напряжениям
Постоянная Подставляя (1.17) в (1.16), имеем
или
Равенство (1.19), как и эквивалентное ему равенство (1.18), носит название закона Гука при растяжении. К примеру, если оба конца стержня закреплены, то его длина неизменна, а деформация
Согласно (1.19) возникающие при этом напряжения равны
Следовательно, когда приращение температуры Деформации при растяжении-сжатии и закон Гука
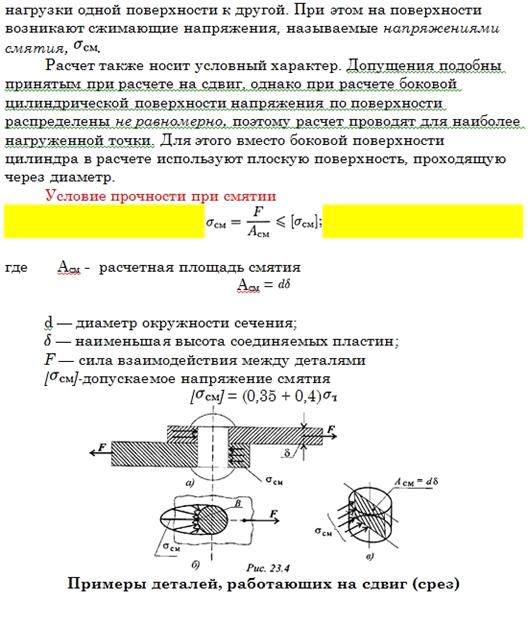
Срез и смятие. Основные допущения на срез и смятия. Расчет на срез и смятие
|
||||
|
Последнее изменение этой страницы: 2016-08-16; просмотров: 2522; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.108 (0.009 с.) |

 ,
, ,
,  – первоначальная и текущая длина стержня соответственно.
– первоначальная и текущая длина стержня соответственно. вызвано действием растягивающих нормальных напряжений
вызвано действием растягивающих нормальных напряжений  , то относительная деформация
, то относительная деформация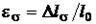
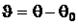 , то деформация
, то деформация



 . (1.16)
. (1.16) ,
, 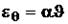 . (1.17)
. (1.17) называется модулем Юнга (модулем растяжения или модулем упругости первого рода), постоянная
называется модулем Юнга (модулем растяжения или модулем упругости первого рода), постоянная  – температурным коэффициентом линейного расширения. Для углеродистых сталей при комнатной температуре модуль Юнга и коэффициент линейного расширения имеют следующий порядок величины:
– температурным коэффициентом линейного расширения. Для углеродистых сталей при комнатной температуре модуль Юнга и коэффициент линейного расширения имеют следующий порядок величины:  (1.18)
(1.18)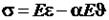 . (1.19)
. (1.19) . Тогда по формуле (1.16) при нагревании (охлаждении) стержня силовая деформация равна и противоположна по знаку тепловой деформации:
. Тогда по формуле (1.16) при нагревании (охлаждении) стержня силовая деформация равна и противоположна по знаку тепловой деформации: .
.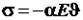 .
. , в стержне действуют сжимающие напряжения:
, в стержне действуют сжимающие напряжения:  . Напротив, в случае
. Напротив, в случае  в стержне возникают растягивающие напряжения:
в стержне возникают растягивающие напряжения:  .
.
 (2) - относительное удлинение или линейные деформации.
(2) - относительное удлинение или линейные деформации. (3) - закон Гука.
(3) - закон Гука.