
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Силы, действующие в сплошных средах. Тензор напряженияСодержание книги
Поиск на нашем сайте
Выделим в сплошной среде объем V, ограниченный поверхностью Массовые силы – силы, действующие на каждый элемент объема dV независимо от того, существуют ли рядом с ним другие части среды (например, силы тяготения). Если Поверхностные силы – силы взаимодействия между отдельными частями сплошной среды. Внутри выделенного объема V эти силы и их моменты уравновешиваются в соответствии с III законом Ньютона, т. е. эти силы остаются приложенными лишь к поверхностным частям объема V (к поверхности Выделим мысленно в среде элементарную треугольную пирамиду, три грани которой параллельны координатным плоскостям, т. е. внешние нормали к этим граням направлены противоположно осям 0 x, 0 y, 0 z декартовой СК. Внешняя нормаль
Объем
Величина вида
Проецируя (8.6.4) на координатные оси, получим:
Проделав то же самое, что и при получении тензора деформации, получим тензор напряжения:
Тензор симметричный, т. е. Существуют три взаимно перпендикулярные оси, для которых
Здесь
т. е. сумма нормальных напряжений на три взаимно перпендикулярные площадки не зависит от ориентации последних. Заметим, что компоненты напряжения выражаются в переменных Эйлера, т. е. являются функциями переменных x, y, z, t. Необходимые уравнения движения сплошных сред Выделим мысленно объем V сплошной среды. Для него
В уравнении (8.7.2) первое слагаемое – главный момент массовых сил и сил инерции, второе слагаемое – главный момент поверхностных сил. Известно, что
Тогда
откуда Учитывая (8.7.3) и то, что
откуда
Здесь первое слагаемое равно нулю (см. (8.7.6)). Из равенства нулю остальных слагаемых (8.7.8) следует:
и Таким образом, второе необходимое уравнение движения сплошной среды указывает, что тензор напряжения симметричен. Уравнения движения сплошной среды в напряжениях в векторной и скалярной формах имеют вид:
При исследовании движения сплошной среды под действием заданных сил компоненты
|
||||
|
Последнее изменение этой страницы: 2016-07-16; просмотров: 347; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.225.255.196 (0.008 с.) |

 . Все силы, действующие на выделенную часть сплошной среды, можно разделить на два класса.
. Все силы, действующие на выделенную часть сплошной среды, можно разделить на два класса. – массовая сила в расчете на единицу массы, то на объем dV с массой
– массовая сила в расчете на единицу массы, то на объем dV с массой  действует массовая сила
действует массовая сила  ; главный вектор этих сил
; главный вектор этих сил  .
. ). Поверхностную силу, действующую на единицу площади, ориентация которой в пространстве задана внешней нормалью
). Поверхностную силу, действующую на единицу площади, ориентация которой в пространстве задана внешней нормалью  , обозначают
, обозначают  и называют напряжением сил на рассматриваемом элементе поверхности. На элемент поверхности
и называют напряжением сил на рассматриваемом элементе поверхности. На элемент поверхности 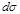 действует поверхностная сила
действует поверхностная сила  ; главный вектор поверхностных сил, действующих на объем V, равен
; главный вектор поверхностных сил, действующих на объем V, равен  . Проекция
. Проекция  – нормальное напряжение (или нормальное давление), проекция
– нормальное напряжение (или нормальное давление), проекция  на площадку, к которой
на площадку, к которой  к четвертой грани составляет с этими осями углы, косинусы которых обозначим
к четвертой грани составляет с этими осями углы, косинусы которых обозначим  . Если площадь этой грани равна
. Если площадь этой грани равна  , то площади остальных граней равны
, то площади остальных граней равны  . Пусть объем пирамиды dV. Тогда на нее действуют массовые силы
. Пусть объем пирамиды dV. Тогда на нее действуют массовые силы  , а массовые силы инерции равны
, а массовые силы инерции равны  , где
, где  – ускорение пирамиды. Поверхностные силы, действующие на грани пирамиды, равны:
– ускорение пирамиды. Поверхностные силы, действующие на грани пирамиды, равны:  ,
,  ,
,  ,
,  . Условие равновесия пирамиды:
. Условие равновесия пирамиды: . (8.6.1)
. (8.6.1) , где h – высота пирамиды. Тогда
, где h – высота пирамиды. Тогда , (8.6.2) и при
, (8.6.2) и при  имеем:
имеем: , (8.6.3)
, (8.6.3) определяет воздействие на соответствующую грань частиц среды, находящихся вне пирамиды. На эти частицы со стороны пирамиды действует сила
определяет воздействие на соответствующую грань частиц среды, находящихся вне пирамиды. На эти частицы со стороны пирамиды действует сила  . Тогда напряжение
. Тогда напряжение  при произвольной ориентации внешней нормали может быть определено, если известны напряжения в той же точке для площадок, внешние нормали которых сонаправлены с осями координат 0 x, 0 y, 0 z:
при произвольной ориентации внешней нормали может быть определено, если известны напряжения в той же точке для площадок, внешние нормали которых сонаправлены с осями координат 0 x, 0 y, 0 z: . (8.6.4)
. (8.6.4) (8.6.5)Здесь
(8.6.5)Здесь  – компоненты напряжения. Пусть
– компоненты напряжения. Пусть  – проекция
– проекция  на произвольное направление
на произвольное направление 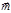 , характеризуемое направляющими косинусами
, характеризуемое направляющими косинусами  . Тогда
. Тогда


 . (8.6.5)
. (8.6.5) . (8.6.6)
. (8.6.6) ,
,  ,
,  . Итак, напряжение в данной точке – функция 6 величин:
. Итак, напряжение в данной точке – функция 6 величин:  ,
, 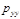 ,
,  ,
,  ,
,  ,
,  .
.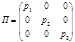 . (8.6.7)
. (8.6.7) – главные напряжения.
– главные напряжения. , (8.6.8)
, (8.6.8)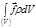 ,
,  ,
,  – главные векторы массовых сил, сил инерции и поверхностных сил. Необходимые уравнения движения выделенного объема
– главные векторы массовых сил, сил инерции и поверхностных сил. Необходимые уравнения движения выделенного объема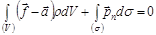 , (8.7.1)
, (8.7.1) . (8.7.2)
. (8.7.2) . (8.7.3)
. (8.7.3) , (8.7.4) и из (8.7.1) получаем:
, (8.7.4) и из (8.7.1) получаем: , (8.7.5)
, (8.7.5) . (8.7.6)
. (8.7.6) ,
,  ,
,  , уравнение (8.7.2) можно преобразовать к виду (см. подробнее в [1, с. 40]):
, уравнение (8.7.2) можно преобразовать к виду (см. подробнее в [1, с. 40]):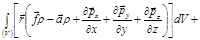
 , (8.7.7)
, (8.7.7) . (8.7.8)
. (8.7.8) (8.7.9)
(8.7.9) ,
,  . (8.7.10)
. (8.7.10) ; (8.7.11)
; (8.7.11) (8.7.12)
(8.7.12) известны, а величины
известны, а величины  подлежат определению. В системе (8.7.12) 3 уравнения с 10 неизвестными, т. е. это необходимые, но не достаточные уравнения. Недостающие уравнения в принципе не могут быть найдены методами классической механики – необходимо знание характеристик среды.
подлежат определению. В системе (8.7.12) 3 уравнения с 10 неизвестными, т. е. это необходимые, но не достаточные уравнения. Недостающие уравнения в принципе не могут быть найдены методами классической механики – необходимо знание характеристик среды.


