
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Импульса механической системыСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Рассмотрим свободную от связей (все связи заменены соответствующими силами) механическую систему, на частицы которой действуют потенциальные силы. Обобщенными координатами для такой системы могут служить декартовы координаты ее частиц. Центром масс или центром инерции механической системы называется воображаемая точка, которая как бы обладает массой всей системы, и положение которой определяется радиус-вектором
где
Импульсом механической системы называется величина, определяемая суммой импульсов всех частиц системы:
Легко видеть, что В ИСО величина, определяемая произведением массы частицы на ее ускорение, равна силе, приложенной к частице (второй закон Ньютона):
тогда где Теорема об изменении импульса системы: производная импульса механической системы по времени равна главному вектору внешних сил
Отсюда следует закон сохранения импульса: если главный вектор внешних сил равен нулю, то импульс механической системы сохраняется:
В частности, это выполняется для замкнутой системы. Если равна нулю какая-либо проекция главного вектора внешних сил, то сохраняется соответствующая проекция импульса механической системы Следствие закона сохранения импульса – постоянство скорости центра инерции замкнутой системы (или постоянство проекции скорости центра инерции при сохранении соответствующей проекции импульса):
Центр масс замкнутой системы движется равномерно и прямолинейно (или покоится), а внутренние потенциальные силы не могут изменить его скорость. Импульс механической системы имеет различные значения в разных системах отсчета. Если система отсчета
Легко видеть, что если импульс в некоторой системе отсчета равен нулю, то скорость этой системы отсчета совпадает со скоростью центра масс системы тел: Таким образом, в системе центра инерции (СЦИ) импульс системы тел равен нулю (что полезно для упрощения решения ряда задач механики). Моментом импульса механической системы называется величина, определяемая геометрической суммой моментов импульсов всех частиц системы (относительно общего начала):
Момент импульса частицы зависит от выбора начала отсчета (полюса). Если полюс совпадает с началом координат, то
где Если
(3.2.15)
Используем (3.2.15) для нахождения зависимости момента импульса системы частиц от выбора полюса см рисунок. Легко видеть, что момент импульса системы Если
Второе и третье слагаемые в (3.2.17) равны нулю, т. к.
где Теорема об изменении момента импульса отдельной частицы выражается формулой:
где
В системе частиц суммарный момент внутренних сил равен нулю. Суммируя (3.2.19), находим:
где Закон сохранения момента импульса: если главный момент внешних сил равен нулю, то момент импульса механической системы сохраняется:
В частности, это выполняется для замкнутой системы. Очевидно, что если Итак, из законов сохранения импульса и момента импульса имеем шесть первых интегралов движения:
Для замкнутой системы имеют место все шесть интегралов движения (3.2.24); для незамкнутой системы могут иметь место некоторые из них. Рассмотренные здесь законы сохранения импульса и момента импульса – частные случаи закона сохранения обобщенного импульса.
|
||||
|
Последнее изменение этой страницы: 2016-07-16; просмотров: 647; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.144.40.182 (0.01 с.) |

 (3.2.1)
(3.2.1) – масса всей системы,
– масса всей системы,  и
и  – масса и радиус-вектор
– масса и радиус-вектор  -й частицы. Скорость и ускорение центра масс даются формулами:
-й частицы. Скорость и ускорение центра масс даются формулами: (3.2.2)
(3.2.2)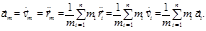 (3.2.3)
(3.2.3) (3.2.4)
(3.2.4)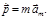 (3.2.5)
(3.2.5) (3.2.6)
(3.2.6) (3.2.7)
(3.2.7) – геометрическая сумма всех сил, действующих на частицы системы. Различают внешние и внутренние силы, причем геометрическая сумма внутренних сил равна нулю, в соответствии с третьим законом Ньютона. Тогда
– геометрическая сумма всех сил, действующих на частицы системы. Различают внешние и внутренние силы, причем геометрическая сумма внутренних сил равна нулю, в соответствии с третьим законом Ньютона. Тогда  в (3.2.7) – геометрическая сумма только внешних сил (главный вектор внешних сил), действующих на частицы системы.
в (3.2.7) – геометрическая сумма только внешних сил (главный вектор внешних сил), действующих на частицы системы. (3.2.8)
(3.2.8) (3.2.9)
(3.2.9) .
. (3.2.10)
(3.2.10) движется относительно системы отсчета
движется относительно системы отсчета  со скоростью
со скоростью  поступательно, то скорости
поступательно, то скорости  -й частицы по отношению к этим системам отсчета связаны соотношением
-й частицы по отношению к этим системам отсчета связаны соотношением  . Тогда
. Тогда (3.2.11)
(3.2.11) (3.2.12)
(3.2.12) (3.2.13)
(3.2.13) (3.2.14)
(3.2.14) – моменты импульсов
– моменты импульсов  -й частицы относительно координатных осей (проекции момента импульса
-й частицы относительно координатных осей (проекции момента импульса  на координатные оси).
на координатные оси). , то
, то

 (3.2.16), где
(3.2.16), где  - импульс системы частиц.
- импульс системы частиц. – центр масс системы, то
– центр масс системы, то  ,
,  ,
, 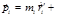
 , и момент импульса системы частиц
, и момент импульса системы частиц (3.2.17)
(3.2.17) и
и  (импульс с СЦИ и координаты центра инерции в СЦИ раны нулю). Тогда
(импульс с СЦИ и координаты центра инерции в СЦИ раны нулю). Тогда (3.2.18)
(3.2.18) – собственный момент импульса системы частиц (относительно центра инерции),
– собственный момент импульса системы частиц (относительно центра инерции), 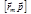 – момент импульса, выражающий движение системы частиц как целого.
– момент импульса, выражающий движение системы частиц как целого.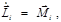 (3.2.19)
(3.2.19) – суммарный момент сил, действующих на частицу
– суммарный момент сил, действующих на частицу (3.2.20)
(3.2.20) (3.2.21)
(3.2.21) (3.2.22)
(3.2.22) – главный момент внешних сил, действующих на механическую систему
– главный момент внешних сил, действующих на механическую систему  . Теорема об изменении момента импульса системы: производная момента импульса механической системы по времени равна главному моменту внешних сил.
. Теорема об изменении момента импульса системы: производная момента импульса механической системы по времени равна главному моменту внешних сил.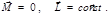 (3.2.23)
(3.2.23) , то
, то  .
.
 (3.2.24)
(3.2.24)


