
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Свободные и вынужденные одномерные колебанияСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Рассмотрим механическую систему с одной степенью свободы и исследуем ее малые колебания вблизи положения устойчивого равновесия. Система имеет только одну обобщенную координату
При малом отклонении
Выбор нулевого состояния для
Это означает, что на систему действует квазиупругая сила
Кинетическая энергия системы с одной степенью свободы
где Функция Лагранжа для системы, совершающей малые гармонические колебания (для одномерного гармонического осциллятора), имеет вид:
Подставляя в уравнение Лагранжа
Общее решение уравнения (5.1.8) может быть представлено в виде
Произвольные постоянные Итак, вблизи положения равновесия система совершает гармонические колебания с амплитудой Частота – основная характеристика колебаний, не зависящая от начальных условий движения и всецело определяемая свойствами механической системы как таковой (см. (5.1.8)). Отметим, что это свойство частоты связано с малостью колебаний и исчезает при переходе к более высоким приближениям. С математической точки зрения это свойство связано с квадратичной зависимостью Энергия системы при малых колебаниях
т. е. энергия пропорциональна квадрату амплитуды. Иногда удобно записывать зависимость вернемся к выражению (5.1.10). Модуль Перейдем к рассмотрению колебаний в системе, подверженной действию внешнего переменного поля; такие колебания называют вынужденными в отличие от рассмотренных выше свободных колебаний. Т. к. рассматриваются малые колебания, то и внешнее поле полагаем достаточно слабым (иначе оно могло бы вызывать большие Итак, наряду с собственной потенциальной энергией Первое слагаемое в (5.1.15) можно не включать в выражение для лагранжиана (его можно рассматривать как полную производную по Подставляя в уравнение Лагранжа, находим уравнение движения:
Здесь Общее решение неоднородного линейного дифференциального уравнения (5.1.18) с постоянными коэффициентами имеет вид: Особый интерес представляет случай, когда вынуждающая сила – простая периодическая функция времени с частотой
Произвольные постоянные Итак, под действием периодической вынуждающей силы система совершает движение, представляющее совокупность двух колебаний – с собственной частотой системы Решение (5.1.23) неприемлемо при Рассмотрим малые колебания вблизи резонанса, т.е. при
В простейшем случае полагаем в (5.1.23)
Если
Поскольку можно считать медленно изменяющейся по синусоидальному закону амплитудой колебаний системы с собственной частотой При резонансе вид функции
Амплитуда таких колебаний линейно расчет со временем, и при
Затухающие колебания До сих пор мы подразумевали, что движение тел происходит в пустоте или, по крайней мере, можно пренебречь влиянием среды на это движение. В действительности при движении тела в среде последняя оказывает сопротивление, стремящееся замедлить движение; механическая энергия движущегося тела при этом переходит в тепловую энергию (диссипируется). В этих условиях процесс движения уже не чисто механический, а его рассмотрение требует учета движения среды и внутреннего теплового состояния как среды, так и тела. В общем случае задача о движении тела в среде выходит за рамки механики. Однако в ряде случаев движение тела в среде может быть описано с помощью механических уравнений движения путем введения в них некоторых дополнительных членов. Сюда относятся колебания с частотами, малыми по сравнению с характерными для внутренних диссипативных процессов в среде частотами. При выполнении этого условия можно считать, что на тело действует сила трения, зависящая только от его скорости для заданной однородной среды. При малых скоростях эта сила трения пропорциональна скорости. Тогда дифференциальное уравнение движения в случае малых колебаний имеет вид:
где Обозначим тогда
где
При этом возможны следующие случаи: 1) 1)
Здесь комплексно-сопряженные числа. Тогда
убывает с течением времени по экспоненциальному закону (рисунок 5.3.1).
Рисунок 5.3.1 Скорость убывания амплитуды характеризуется коэффициентом затухания
При малых значениях
Таким образом Затухающие колебания характеризуются декрементом затухания – отношением двух значений амплитуды, измеренных в моменты времени, разделенные условным периодом
Но чаще используют логарифмический декремент затухания
Несложно убедиться, что логарифмический декремент затухания – величина, обратная числу колебаний
Полная энергия системы
2)
Такое движение называют апериодическим затуханием. Два возможных варианта такого движения представлены на рисунке 5.3.2.
Рисунок 5.3.2 Рисунок 5.3.3 3)
Для системы с несколькими степенями свободы обобщенные силы трения, соответствующие координатам Механические соображения не позволяют сделать вывод о симметричности коэффициентов Тогда выражения (5.3.20) могут быть записаны в виде производных
Силы (5.3.23) должны быть добавлены к правой части уравнений Лагранжа:
Диссипативная функция определяет интенсивность диссипации энергии в системе (можно показать, что скорость изменения энергии Уравнения колебаний при наличии трения имеют вид:
Положив в этих уравнениях получим систему линейных алгебраических уравнений для определения постоянных
Характеристическое уравнение этой системы – уравнение степени
Поскольку все коэффициенты этого уравнения вещественны, то его корни либо вещественны, либо попарно комплексно сопряжены. При этом вещественные корни непременно отрицательны, а комплексные имеют отрицательную вещественную часть (в противном случае координаты и скорости, а значит, и энергия возрастали бы экспоненциально, в то время как наличие диссипативных сил должно приводить к уменьшению энергии).
|
|||||||||||||||||
|
Последнее изменение этой страницы: 2016-07-16; просмотров: 476; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.142.201.93 (0.009 с.) |

 . Пусть в положении равновесия
. Пусть в положении равновесия  . Тогда соответствующая координате
. Тогда соответствующая координате  обобщенная сила
обобщенная сила  при
при  обращается в нуль. Если сила потенциальная, то
обращается в нуль. Если сила потенциальная, то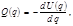 (5.1.1) где
(5.1.1) где  – потенциальная энергия, имеющая экстремум в положении равновесия. При устойчивом равновесии
– потенциальная энергия, имеющая экстремум в положении равновесия. При устойчивом равновесии  и
и 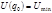 .
. от положения равновесия
от положения равновесия  , и потенциальная энергия
, и потенциальная энергия (5.1.2)
(5.1.2) произволен, поэтому можно положить
произволен, поэтому можно положить . Равновесие при
. Равновесие при  ,
,  , т. е.
, т. е.  (5.1.3)
(5.1.3)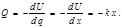 (5.1.4)
(5.1.4) (5.1.5)
(5.1.5) – коэффициент инерции (постоянная или медленно меняющаяся функция
– коэффициент инерции (постоянная или медленно меняющаяся функция  ). Для малых смещений можно считать
). Для малых смещений можно считать  . Подчеркнем, что
. Подчеркнем, что  совпадает с массой только в том случае, когда
совпадает с массой только в том случае, когда  – декартова координата частицы, характеризующей (заменяющей) движущуюся систему.
– декартова координата частицы, характеризующей (заменяющей) движущуюся систему. (5.1.6)
(5.1.6) , находим уравнение движения:
, находим уравнение движения:  (5.1.7) или
(5.1.7) или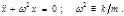 (5.1.8)
(5.1.8)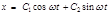 (5.1.9) или
(5.1.9) или (5.1.10)
(5.1.10) и
и  связаны с постоянными
связаны с постоянными  и
и  соотношениями:
соотношениями: 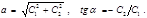 (5.1.11)
(5.1.11) ;
;  – начальное значение фазы, зависящее от выбора начала отсчета времени,
– начальное значение фазы, зависящее от выбора начала отсчета времени,  – циклическая частота колебаний (в теоретической физике ее называют обычно просто частотой).
– циклическая частота колебаний (в теоретической физике ее называют обычно просто частотой). от
от  .
. (5.1.12)
(5.1.12) в виде вещественной части комплексного выражения:
в виде вещественной части комплексного выражения:  (5.1.13) где
(5.1.13) где  – комплексная амплитуда. Записав ее в виде
– комплексная амплитуда. Записав ее в виде  (5.1.14)
(5.1.14)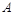 совпадает с обычной амплитудой, аргумент – с начальной фазой.
совпадает с обычной амплитудой, аргумент – с начальной фазой. ).
). необходимо рассматривать еще некоторое слагаемое
необходимо рассматривать еще некоторое слагаемое  , связанное с действием внешнего поля. При малых
, связанное с действием внешнего поля. При малых  (5.1.15)
(5.1.15) от некоторой другой функции времени). Во втором слагаемом
от некоторой другой функции времени). Во втором слагаемом  есть внешняя «сила», действующая на систему в положении равновесия и являющаяся заданной функцией времени; обозначим ее
есть внешняя «сила», действующая на систему в положении равновесия и являющаяся заданной функцией времени; обозначим ее  . Тогда лагранжиан системы
. Тогда лагранжиан системы  (5.1.16)
(5.1.16) (5.1.17)или
(5.1.17)или  (5.1.18)
(5.1.18) – по-прежнему частота свободных колебаний.
– по-прежнему частота свободных колебаний. (5.1.19)где
(5.1.19)где  – общее решение соответствующего однородного уравнения (см. (5.1.10)),
– общее решение соответствующего однородного уравнения (см. (5.1.10)),  – частное решение уравнения (5.1.18).
– частное решение уравнения (5.1.18). :
: (5.1.20)Тогда частотный интеграл (5.1.18) ищем в виде:
(5.1.20)Тогда частотный интеграл (5.1.18) ищем в виде:  (5.1.21)Подстановка в (5.1.18) дает:
(5.1.21)Подстановка в (5.1.18) дает:  (5.1.22) и (5.1.9) можно переписать в виде:
(5.1.22) и (5.1.9) можно переписать в виде:  (5.1.23)
(5.1.23) и
и  определяются из начальных условий.
определяются из начальных условий. и с частотой вынуждающей силы
и с частотой вынуждающей силы 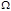 .
. (так называемый резонанс –
(так называемый резонанс – 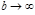 ). Это вполне естественно, т. к. при больших значениях
). Это вполне естественно, т. к. при больших значениях  колебания перестают быть малыми, и вся изложенная выше теория перестает быть применимой.
колебания перестают быть малыми, и вся изложенная выше теория перестает быть применимой. , где
, где  . Тогда
. Тогда . (5.1.24)
. (5.1.24) . Тогда
. Тогда (5.1.25)
(5.1.25) , то
, то  и
и (5.1.26)
(5.1.26) , то функцию
, то функцию  (5.1.27)
(5.1.27) . Это так называемые биения, полученные при сложении колебаний с близкими частотами. Нечто подобное, хотя математически и более сложное, получается при
. Это так называемые биения, полученные при сложении колебаний с близкими частотами. Нечто подобное, хотя математически и более сложное, получается при  и
и  .
. изменяется:
изменяется: (5.1.28) и
(5.1.28) и  (5.1.29)
(5.1.29) отклонения могут быть сколь угодно большими – система разрушается.
отклонения могут быть сколь угодно большими – система разрушается. (5.3.1)
(5.3.1) – коэффициент сопротивления (определяется свойствами среды и формой тела; например, в формуле Стокса
– коэффициент сопротивления (определяется свойствами среды и формой тела; например, в формуле Стокса  , где
, где  – вязкость,
– вязкость, 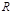 – радиус движущегося в вязкой среде шара). При
– радиус движущегося в вязкой среде шара). При  решением (5.3.1) будет
решением (5.3.1) будет  , где
, где  ,
,  (5.3.2)
(5.3.2) (5.3.3)
(5.3.3) – коэффициент затухания. Это однородное дифференциальное уравнение второго порядка, общее решение которого можно представить в виде
– коэффициент затухания. Это однородное дифференциальное уравнение второго порядка, общее решение которого можно представить в виде (5.3.4)
(5.3.4) – корни характеристического уравнения
– корни характеристического уравнения (5.3.5)
(5.3.5) ; 2)
; 2)  ; 3)
; 3) 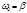 . Рассмотрим каждый из них.
. Рассмотрим каждый из них. – силы трения меньше квазиупругих сил.
– силы трения меньше квазиупругих сил. (5.3.6)
(5.3.6) (5.3.7)
(5.3.7) (5.3.8)
(5.3.8) (5.3.9)(использована формула Эйлера
(5.3.9)(использована формула Эйлера  ). Полученное уравнение описывает колебательное движение тела (частицы), амплитуда которого
). Полученное уравнение описывает колебательное движение тела (частицы), амплитуда которого  (5.3.10)
(5.3.10)
 ; за время релаксации
; за время релаксации  амплитуда уменьшается в
амплитуда уменьшается в  раз. Это не периодический процесс, т. к. нельзя указать период
раз. Это не периодический процесс, т. к. нельзя указать период  , для которого
, для которого  . Но периодичность есть в том смысле, что через равные промежутки времени
. Но периодичность есть в том смысле, что через равные промежутки времени  система проходит через положение равновесия, двигаясь в одну и ту же сторону.
система проходит через положение равновесия, двигаясь в одну и ту же сторону.  – условный период затухающих колебаний:
– условный период затухающих колебаний: (5.3.11)
(5.3.11) и
и (5.3.12)
(5.3.12) , что вполне очевидно, действие сил трения замедляет движение.
, что вполне очевидно, действие сил трения замедляет движение. (5.3.13)
(5.3.13)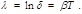 (5.3.14)
(5.3.14) за время релаксации
за время релаксации  :
: (5.3.15)
(5.3.15)



 (5.3.16) где
(5.3.16) где  – начальное значение энергии. При
– начальное значение энергии. При  имеем
имеем (5.3.17)т. е. запас энергии убывает быстрее амплитуды.
(5.3.17)т. е. запас энергии убывает быстрее амплитуды. – силы трения больше квазиупругих сил. Оба корня характеристического уравнения вещественны и отрицательны. Движение системы состоит в асимптотическом приближении к положению равновесия по закону
– силы трения больше квазиупругих сил. Оба корня характеристического уравнения вещественны и отрицательны. Движение системы состоит в асимптотическом приближении к положению равновесия по закону (5.3.18)
(5.3.18)

 – особый случай апериодического затухания (см. рисунок 5.3.3):
– особый случай апериодического затухания (см. рисунок 5.3.3): (5.3.19)
(5.3.19) , являются линейными функциями скоростей вида
, являются линейными функциями скоростей вида  (5.3.20)
(5.3.20) по индексам, но в статистической физике доказывается, что
по индексам, но в статистической физике доказывается, что  (5.3.21)
(5.3.21) от квадратичной формы, называемой диссипативной функцией
от квадратичной формы, называемой диссипативной функцией  (5.3.23)
(5.3.23) (5.3.24)
(5.3.24)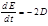 ). Поскольку при уменьшении энергии
). Поскольку при уменьшении энергии  , то квадратичная форма (5.3.23) существенно положительна.
, то квадратичная форма (5.3.23) существенно положительна. (5.3.25)
(5.3.25) (5.3.26)
(5.3.26) :
: (5.3.27)
(5.3.27) относительно
относительно  :
: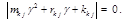 (5.3.28)
(5.3.28)


