
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Рассеяние частиц. Формула РезерфордаСодержание книги
Поиск на нашем сайте В предыдущем подразделе рассмотрено упругое рассеяние частиц, взаимодействующих только при столкновении. Рассмотрим подобную задачу для частиц, взаимодействующих на расстоянии, в случае, когда между ними действуют силы отталкивания. В соответствии с общим правилом рассматриваем сначала эквивалентную задачу об отклонении одной частицы массой
Рисунок 4.5.1 Траектория частицы в центральном поле симметрична по отношению к прямой, проведенной из полюса к ближайшей точке траектории (ОА на рисунке 4.5.1). Обе асимптоты траектории пересекают эту прямую под одинаковыми углами
Используя общую формулу (4.2.18), для угла
Здесь интеграл берется между ближайшим к центру и бесконечно удаленным положениями частицы. При имеющем здесь место инфинитном движении удобно ввести вместо постоянных Е и L другие: скорость
Тогда Вместе с (4.5.1), эта формула определяет зависимость При рассеянии пучка одинаковых частиц, падающих на рассеивающий центр с одинаковой скоростью
имеет размерность площади и называется дифференциальным сечением рассеяния. Эта величина всецело определяется видом рассеивающего поля и является важной характеристикой процесса рассеяния. Считаем, что угол рассеяния Для нахождения зависимости
или, используя телесный угол
Заметим, что если функция Выражение (4.5.7) определяет дифференциальное сечением рассеяния в зависимости от угла рассеяния в системе центра инерции. Для нахождения дифференциального сечения в зависимости от угла рассеяния Одно из важнейших применений полученных выше формул – рассеяние заряженных частиц в кулоновском поле. При откуда Учитывая, что
Дифференцируя по
Это так называемая формула Резерфорда. Полученный результат не зависит от знака В л-системе для первоначально покоившихся частиц, подставляя
Для двигавшихся первоначально частиц преобразование в общем случае дает громоздкую формулу для где
Если не только массы равны, но и частицы тождественны, то не имеет смысла различать после рассеяния первоначально двигавшиеся и покоившиеся частицы. Общее дифференциальное сечение рассеяния для всех частиц в этом случае
где С помощью общей формулы (4.5.12) можно получить также выражение для дифференциального сечения рассеяния как функции потери энергии Заметим, что вычисление дифференциального сечения рассеяния значительно упрощается для больших прицельных расстояний (поле слабое и углы отклонения малы).
|
||
|
Последнее изменение этой страницы: 2016-07-16; просмотров: 532; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.214 (0.01 с.) |

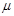 в поле
в поле 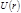 неподвижного силового центра, расположенного в центре инерции системы частиц.
неподвижного силового центра, расположенного в центре инерции системы частиц.
 . Угол отклонения частицы при ее пролете мимо силового центра (рисунок 4.5.1
. Угол отклонения частицы при ее пролете мимо силового центра (рисунок 4.5.1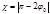 . (4.5.1)
. (4.5.1)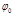 запишем:
запишем: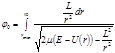 . (4.5.2)
. (4.5.2) частицы на бесконечности и так называемое прицельное расстояние
частицы на бесконечности и так называемое прицельное расстояние 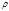 , на котором частица пролетела бы мимо центра, если бы силовое поле отсутствовало (рисунок 4.5.1). Энергия и момент импульса выражаются через эти величины:
, на котором частица пролетела бы мимо центра, если бы силовое поле отсутствовало (рисунок 4.5.1). Энергия и момент импульса выражаются через эти величины: ,
,  . (4.5.3)
. (4.5.3)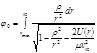 . (4.5.4)
. (4.5.4) от
от  .
.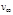 , разные частицы пучка имеют разные прицельные расстояния и, соответственно, разные углы рассеяния. Пусть
, разные частицы пучка имеют разные прицельные расстояния и, соответственно, разные углы рассеяния. Пусть 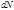 – число частиц, рассеиваемых в единицу времени на углы в интервале
– число частиц, рассеиваемых в единицу времени на углы в интервале 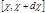 . Если n – число частиц, проходящих в единицу времени через единицу площади поперечного сечения падающего (однородного по сечению) пучка, то величина
. Если n – число частиц, проходящих в единицу времени через единицу площади поперечного сечения падающего (однородного по сечению) пучка, то величина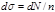 (4.5.5)
(4.5.5)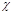 – монотонно убывающая функция прицельного расстояния
– монотонно убывающая функция прицельного расстояния 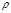 . Тогда в заданный интервал углов
. Тогда в заданный интервал углов  рассеиваются лишь те частицы, которые летят в интервале прицельных расстояний
рассеиваются лишь те частицы, которые летят в интервале прицельных расстояний 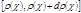 . Число таких частиц
. Число таких частиц 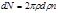 (произведение n на площадь кольца с радиусами
(произведение n на площадь кольца с радиусами  ). Тогда
). Тогда 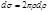 . (4.5.6)
. (4.5.6) от
от  перепишем (4.5.6) в виде:
перепишем (4.5.6) в виде: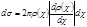 , (4.5.7)
, (4.5.7)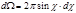 ,
,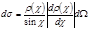 . (4.5.8)
. (4.5.8) многозначна, то под
многозначна, то под 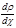 понимают сумму таких выражений по всем ветвям функции
понимают сумму таких выражений по всем ветвям функции 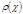 .
. в л-системе необходимо выразить
в л-системе необходимо выразить  по формулам (4.4.14). При этом получаются выражения как для сечения рассеяния падающего пучка, так и для первоначально покоившихся частиц.
по формулам (4.4.14). При этом получаются выражения как для сечения рассеяния падающего пучка, так и для первоначально покоившихся частиц. интеграл в (4.5.4) берется:
интеграл в (4.5.4) берется: 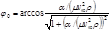 (4.5.9)
(4.5.9)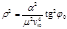 . (4.5.10)
. (4.5.10)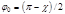 , имеем:
, имеем: . (4.5.11)
. (4.5.11)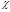 и подставляя в (4.5.7) или (4.5.8), находим:
и подставляя в (4.5.7) или (4.5.8), находим: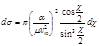 (4.5.12) или
(4.5.12) или  . (4.5.13)
. (4.5.13)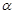 , т. е. применим как для поля отталкивания, так и для поля притяжения. Формулы (4.5.12) и (4.5.13) получены в ц-системе.
, т. е. применим как для поля отталкивания, так и для поля притяжения. Формулы (4.5.12) и (4.5.13) получены в ц-системе.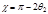 в (4.5.12), получаем:
в (4.5.12), получаем: . (4.5.14)
. (4.5.14)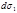 . При
. При 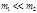 имеем
имеем 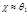 ,
,  и
и 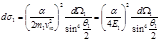 , (4.5.15)
, (4.5.15) – энергия двигавшейся первоначально частицы. При
– энергия двигавшейся первоначально частицы. При 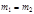 имеем
имеем  ,
, 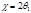 и
и (4.5.16)
(4.5.16) (4.5.17)
(4.5.17)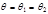 – общий угол рассеяния.
– общий угол рассеяния. (см. подробнее в [2, с. 69]):
(см. подробнее в [2, с. 69]):  . (4.5.18)
. (4.5.18)


