
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Уравнение движения частицы относительно ИСО. ПринципСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте Механической причинности Дифференциальное уравнение движения частицы массой m в силовом поле в векторной форме записи имеет вид:
Это основное уравнение нерелятивистской динамики частицы. Оно может рассматриваться как исходное положение (постулат), из которого путем математических преобразований получают как общие следствия и выводы классической механики, так и решения ее конкретных задач. Все механические движения подчиняются этому уравнению, в котором m – скалярный параметр, характеризующий свойства частицы, С помощью данного уравнения ставятся и решаются две важнейшие задачи динамики частицы. Первая задача (или прямая задача): дан закон движения Задача решается двойным дифференцированием по времени кинематического уравнения движения Вторая (обратная) задача: известно силовое поле, в котором движется частица массой m; требуется найти закон движения частиц. Приведем алгоритм решения обратной задачи динамики частицы в декартовых координатах. Известно
Общее решение этой системы уравнений имеет вид:
где Наличие произвольных постоянных в общем интеграле показывает, что он представляет не конкретное движение, а дает кинематические уравнения непрерывного семейства движений с одинаковыми ускорениями. Например, кинематические уравнения и траектории движения частицы под действием силы тяжести зависят от начальных условий (тела, брошенные вертикально вверх, горизонтально, под углом к горизонту движутся по-разному), хотя динамическое уравнение движения
а также
(1.7.4) и (1.7.5) образуют систему из шести независимых уравнений, из которых можно выразить постоянные
Таким образом, обратная задача динамики частицы решена. Заметим, что зачастую дифференциальные уравнения движения можно решить лишь с использованием численных методов. Полное решение второй задачи динамики не требуется, если известны первые интегралы движения. Рассмотрим смысл первых интегралов. Добавляя к (1.7.3) уравнения
получим систему уравнений относительно неизвестных
Выражая из последнего уравнения время t и подставляя его значение в остальные уравнения, получим:
Поскольку Знание некоторых интегралов движения сразу дает ответы на частные вопросы. Поэтому установление признаков существования интегралов дви-жения и их нахождение – важная задача динамики частицы. Основное уравнение динамики и общий анализ его решения позволяют установить причинно-следственные связи при механическом движении. Состояние механической системы считается в данный момент заданным, если известны массы каждой частицы, координаты и скорости. Можно утверждать, что состояние в данный момент времени предопределяет (причем однозначно) состояние данной системы в любой другой момент времени. Такая однозначная связь причины и следствия носит название динамической закономерности. Классическая механика относится к теориям с динамической закономерной связью между причинами и следствиями. Принцип механической причинности в классической механике: состояние системы материальных точек однозначно определяется их взаимодействием и начальными условиями.
|
||
|
Последнее изменение этой страницы: 2016-07-16; просмотров: 652; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.41 (0.01 с.) |

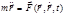 . (1.7.1)
. (1.7.1)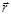 – радиус-вектор,
– радиус-вектор, 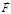 – некоторая однозначная, конечная и непрерывная функция координат, скорости и времени, которая может быть определена независимо. Постулируется именно этот общий вид уравнения (то, что его правую часть называют силой, ничего от объективности закона движения не отнимает).
– некоторая однозначная, конечная и непрерывная функция координат, скорости и времени, которая может быть определена независимо. Постулируется именно этот общий вид уравнения (то, что его правую часть называют силой, ничего от объективности закона движения не отнимает).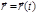 частицы массой m; требуется найти действующую на частицу силу.
частицы массой m; требуется найти действующую на частицу силу.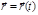 и подстановкой полученного выражения
и подстановкой полученного выражения  в основное уравнение динамики. В результате получаем некоторую функциональную зависимость
в основное уравнение динамики. В результате получаем некоторую функциональную зависимость  . Используя уравнения
. Используя уравнения 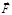 в различных точках пространства, т. е. определить вид силового поля. Прямая задача динамики сравнительно простая, требует применения методов только дифференциального исчисления и всегда имеет решение.
в различных точках пространства, т. е. определить вид силового поля. Прямая задача динамики сравнительно простая, требует применения методов только дифференциального исчисления и всегда имеет решение. , т. е. известны проекции
, т. е. известны проекции 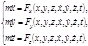 (1.7.2)
(1.7.2)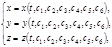 (1.7.3)
(1.7.3)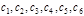 – произвольные постоянные. В простейших случаях переменные в уравнениях (1.7.2) разделяются, и решение сводится к последовательному взятию двух неопределенных интегралов (квадратурам). Поэтому общее решение иногда называют интегралом уравнений, хотя в общем случае решение к квадратурам не сводится.
– произвольные постоянные. В простейших случаях переменные в уравнениях (1.7.2) разделяются, и решение сводится к последовательному взятию двух неопределенных интегралов (квадратурам). Поэтому общее решение иногда называют интегралом уравнений, хотя в общем случае решение к квадратурам не сводится. одно и то же для всех случаев. Таким образом, задание силы не определяет однозначно движение частицы: под действием одной и той же силы частица может совершать любые движения из семейства, описанного формулами (1.7.3). Чтобы обратная задача динамики имела определенное решение, необходимы добавочные начальные условия, например:
одно и то же для всех случаев. Таким образом, задание силы не определяет однозначно движение частицы: под действием одной и той же силы частица может совершать любые движения из семейства, описанного формулами (1.7.3). Чтобы обратная задача динамики имела определенное решение, необходимы добавочные начальные условия, например: 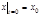 ,
, 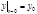 ,
, 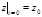 ,
, 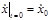 ,
,  ,
, 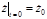 . Положив в (1.7.3) t = 0 и используя начальные условия, получаем:
. Положив в (1.7.3) t = 0 и используя начальные условия, получаем: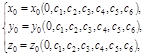 (1.7.4)
(1.7.4)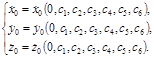 (1.7.5)
(1.7.5)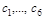 через начальные координаты и скорости:
через начальные координаты и скорости:  и т. д. Подстановка найденных значений
и т. д. Подстановка найденных значений 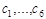 в общее решение (1.7.3) дает частное решение системы дифференциальных уравнений (1.7.2). Это и есть искомые кинематические уравнения движения частицы:
в общее решение (1.7.3) дает частное решение системы дифференциальных уравнений (1.7.2). Это и есть искомые кинематические уравнения движения частицы: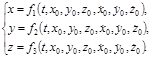 (1.7.6)
(1.7.6)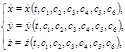 (1.7.7)
(1.7.7)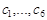 . Предположим, что эта система решена:
. Предположим, что эта система решена: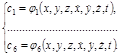 (1.7.8)
(1.7.8)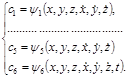 (1.7.9)
(1.7.9)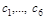 – постоянные, то функции
– постоянные, то функции 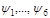 сохраняют свои значения при движении частицы. Они называются первыми интегралами движения и выражают законы сохранения некоторых величин с. Из (1.7.9) следует существование шести независимых первых интегралов. Любая функция первых интегралов также интеграл движения (зависимый). Если все шесть первых интегралов известны, то из них можно без интегрирования получить полное решение второй задачи динамики. Знание одного первого интеграла позволяет упростить решение исходной системы дифференциальных уравнений.
сохраняют свои значения при движении частицы. Они называются первыми интегралами движения и выражают законы сохранения некоторых величин с. Из (1.7.9) следует существование шести независимых первых интегралов. Любая функция первых интегралов также интеграл движения (зависимый). Если все шесть первых интегралов известны, то из них можно без интегрирования получить полное решение второй задачи динамики. Знание одного первого интеграла позволяет упростить решение исходной системы дифференциальных уравнений.


