
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Динамика вращательного движенияСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
МЕХАНИКА Кинематика 1. Кинематические уравнения движения двух материальных точек имеют вид t = 0; 2) а 1 = -4 м/с2; 3) а 2= 2 м/с2) 2. Радиус-вектор материальной точки изменяется со временем по закону (1) u = 6,7 м/с; а = 8,48 м/с2)
3. Зависимость пройденного пути S от времени t дается уравнением S = A – Bt + Ct2, где А = 6 м, В = 3 м/с и С = 2 м/с2. Найти среднюю скорость и среднее ускорение тела в интервале времени от 1 до 4 с. (7м/с, 4 м/с2) 4. Закон движения материальной точки имеет вид x = b1 + c1t, y = c2t + d2t2, z = 0, где b1 = -9 м; с1 = 3 м/с; с2 = 4 м/с; d2 = -1 м/с2. Построить графики зависимости x(t) и y(t) и траекторию точки за первые 5 с движения. Найти векторы скорости, ускорения и угол между ними в момент времени t1 = 2 c и t2 = 4 c. На плоскости XOY построить траекторию движения материальной точки и векторы скорости и ускорения для t1 и t2. 5. Закон движения материальной точки имеет вид x = b1t +d1t3, y = b2t + c2t2, z = 0, где b1 = 27 м/с; d1 = -1 м/с3; b2 = 32 м/с; с2 = -8 м/с2. На плоскости XOY построить траекторию движения точки в первые 6 с. Определить касательное и нормальное ускорения и радиус кривизны траектории в момент времени t1=2c. 6. Материальная точка движется прямолинейно. Модуль её скорости изменяется со временем по закону v = l,0t2, где v - скорость, м/с; t - -время, с. Вычислить путь, пройденный точкой за первые 10 с движения и среднее значение скорости в интервале от 5 до 10 с. (0,33 км; 58 м/с) 7. Два автомобиля, выехали одновременно из одного пункта, движутся прямолинейно в одном направлении. Зависимость пройденного пути задается уравнениями s1 = At + Bt2 и s2 = Ct + Dt2 + Ft3. Определите относительную скорость автомобилей. 8. Велосипедист проехал первую половину времени своего движения со скоростью v1 = 16 км/ч, вторую половину времени – со скоростью v2 = 12 км/ч. Определите среднюю скорость движения велосипедиста. 9. В течение времени τ скорость тела задается уравнением вида v = A+Bt+Ct2 (0≤ t ≤ τ). Определите среднюю скорость за промежуток времени τ. 10. Трамвай движется на прямолинейном участке между остановками с ускорением, изменяющимся по закону а = a0 - bs, где a0 и b - положительные постоянные; s - пройденный путь. Найти расстояние между этими остановками. (2 a0/b.) 11. Частица движется в плоскости хОу из точки с координатами х = у = 0 со скоростью v = a i + bx j, где а и b - некоторые постоянные; i и j - орты осей х и у. Найти уравнение её траектории. (у = (b/2а)х2) 12. Скорость автомобиля при экстренном торможении изменялась по закону v = 49 – 1,0 t2, где v - скорость, м/с; t - время, с. Определить время торможения и тормозной путь. (7,0 с и 0,23 км.) 13. С башни брошено тело в горизонтальном направлении со скоростью 15 м/с. Пренебрегая сопротивлением воздуха, определить радиус кривизны траектории тела через 2 с после начала движения. (0,1 км.) 14. Материальная точка движется по закону r = 4t2 i + 3t j + 2 k, где i, j, k -орты осей x, yt z; r - радиус-вектор, м; t - время, с, Определить: 1)скорость как функцию времени; 2) модуль скорости в момент времени t = 2,0 с; 3) ускорение точки. (16 м/с; в м/с2) 15. Частица движется в плоскости хОу из точки с координатами х = у = 0 со скоростью v = a i + bx j, где а и b - некоторые постоянные; i и j - орты осей х и у. Найти уравнение её траектории. (у = b/2а)х2) 16. Камень, брошенный с высоты h = 2,1 м под углом a = 45о к горизонту. Падает на землю на расстоянии s = 42 м (по горизонтали) от места бросания (см. рис. 1). Найти начальную скорость камня, время полета и максимальную высоту подъема над уровнем земли. Определить также радиусы кривизны траектории в верхней точке и в точке падения камня на землю.
17. При падении камня в колодец его удар о поверхность воды доносится через t = 5 с. Принимая скорость звука u = 330 м/с, определите глубину колодца 18. Колесо вращается с постоянным угловым ускорением e = 3 рад/с2. Определите радиус колеса, если через t = 1 c после начала движения полное ускорение колеса а = 7,5 м/с2. (R = 79 м) 19. Колесо автомашины вращается равнозамедленно. За время t = 2 мин оно изменило частоту вращения от 240 до 60 мин -1. Определите: 1) угловое ускорение колеса; 2) число полных оборотов, сделанных колесом за это время. (1) e = 0,157 рад/с2; 2) N = 300) 20. Скорость тела изменяется по закону (6,0 см/с; 6,0 м/с2)
21. Движение тела задано уравнениями: ( 22. Точка двигалась в течение времени t1 = 15 с со скоростью u1= 5 м/с, в течение t2 — 10 с со скоростью u2 = 8 м/с и в течение t3 = 6 с со скоростью u3 = 20 м/с. Какова средняя путевая скорость u точки? (uср = 8,9м/с) 23. Движение точки по прямой задано уравнением х = 2t — 0,5t2. Определить среднюю путевую скорость uср точки в интервале времени от tl = 1 с до t2 = 3 с. (u = 0,5 м/с) 24. Точка движется по прямой согласно уравнению х = 6t — 0.125t3. Определить среднюю путевую скорость ucp точки в интервале времени от tl = 2 с до t2 = 6 с. (ucp = 3 м/с) 25. Самолет пролетает расстояние s1 = 500 км на восток от города А в город В за t1 = 45 мин, затем поворачивает на юг и преодолевает расстояние s2 = 1000 км от города В до города С за 1,5 ч, Определить: 1) величину и направление вектора перемещения самолета из А в С; 2) величину и направление вектора средней скорости; 3) среднюю путевую скорость. Направление задается азимутом а, т. е. углом между направлением на север и данным вектором, отсчитывается по часовой стрелке, т, е. от севера к востоку (1) 26. За 3,5 ч воздушный шар снесло на s1 = 21,5 км к северу, затем на s2 = 9.,7 км к востоку, причем высота его подъема увеличилась на h = 2,88 км. Найти: 1) величину вектора его средней скорости; 2) угол b вектора средней скорости с горизонтальной плоскостью. (1) 27. Предполагается, что самолет, имеющий скорость u = 550 км/ч, должен лететь по прямой под углом j = 33,0° к северу от направления на восток. Однако с севера дует постоянный ветер со скоростью ul = 120 км/ч. В каком направлении должен лететь самолет? (Под углом a = 43,5° к северу от направления на восток) 28. Определить время полета самолета между двумя пунктами, находящимися на расстоянии s = 500 км, если скорость самолета относительно воздуха u0 = 100 м/с, а скорость встречного ветра, направленного под углом a = 30° к прямой, соединяющей эти пункты, равна u1 = 30 м/с. Во сколько раз уменьшится время полета, если ветер будет попутным, а его скорость направлена под углом a = 30° к направлению движения? Под каким углом к направлению движения должна быть направлена скорость самолета в обоих случаях? (1,9 ч; 1,7 раз; 9°; 9°) 29. Велосипедист начал движение и в течение времени t1 = 5 с ехал с ускорением а = 1 м/с2, затем в течение следующих t2 = 6 с двигался равномерно и последние 25 м - равнозамедленно до остановки. Найти среднюю скорость на всем пути. ( 30. По прямолинейному шоссе ACD едет машина, которой необходимо за кратчайшее время добраться из пункта А в пункт В, расположенный в поле на расстоянии l = 500 м от дороги (смотри первый рисунок). Известно, что скорость машины по полю в n = 2 раза меньше скорости машины по шоссе. На каком расстоянии s от точки D следует свернуть с шоссе? Проанализировать роль расстояния l между пунктами А и D, лежащими на шоссе. (s = 288,7 м; при L < s машина из А сразу должна съехать с шоссе и зять курс на пункт В)
31. Из пункта A, находящегося на шоссе, необходимо попасть за кратчайшее время в пункт B, находящееся в поле на расстоянии D от шоссе. Известно, что скорость машины по полю в n раз меньше скорости по шоссе. На каком расстоянии от точки В следует свернуть с шоссе. 32. Скорость света в вакууме равна c, а в среде v = c/n1, где n1 – абсолютный показатель преломления света. Обосновать закон преломления света. 33. Зависимость пройденного точкой пути от времени задана уравнением s = 0,14t2 + 0,01t3 (здесь и далее в подобных задачах время измеряется в секундах, расстояние — в метрах). Определить: 1) через какое время t1 ускорение точки будет равно а = 1 м/с2; 2) мгновенную скорость ul в этот момент времени; 3) среднюю путевую скорость ucp за промежуток времени от t = 0 до t1. (tl = 12 с; 2) u1, = 7,68 м/с; 3) u ср = 3,12 м/с) 34. Положение объекта на прямой линии в зависимости от времени дается уравнением х = at + bt2 + ct3, где а = -8 м/с; b = 6 м/с2, с = - 1 м/с3. Найти среднюю скорость ( 35. Две материальные точки движутся согласно уравнениям x1 = 4t + 8t2 -16t3; х2 = 2t – 4t2 + t3. В какой момент времени t1 ускорения этих точек будут одинаковы? Найти скорости u1, и u2 точек в этот момент. (t1 = 0,235 с; u2 = 5,11 м/с; u2 = 0,284 м/с) 36. Движение двух материальных точек выражается уравнениями х, = 20 + 4t - 4t2; x2 = 2 + t• 37. + 0,5t2. В какой момент времени t1 скорости этих точек будут одинаковыми? Определить скорости u1 и u2 и ускорения а 1, и а 2 точек в этот момент. (t1 = 0,333 с; u1 = u2 = 1,33 м/с; а 1 = -8 м/с2, а2 = 1 м/с2) 38. Зависимость пройденного телом пути s от времени t дается уравнением s = 1t - 3t2 + 4t3.Найти расстояние, пройденное телом, скорость и ускорение тела через 2 с после начала движения. (s = 24 м; u = 38 м/с; а = 42 м/с2) 39. Замаскированный полицейский автомобиль, движущийся с постоянной скоростью u1 = 80 км/ч, обогнал лихач. Если полицейский автомобиль, ускоряясь равномерно с ускорением а = 3 м/с2, догнал его через время t = 6 с, то какой была скорость лихача? (u = 108 км/ч) 40. Замаскированный полицейский автомобиль, движущийся с постоянной скоростью u1 = 80 км/ч, обогнал лихач, несущийся со скоростью 100 км/ч. Ровно через D t = 1 с после обгона полисмен нажал на акселератор. Если ускорение полицейского автомобиля а = 3 м/с2, то сколько времени понадобится полицейским, чтобы догнать лихача (будем полагать, что он движется с постоянной скоростью)?
41. Автомобиль, движущийся со скоростью u0 = 50 км/ч, врезается в дерево; передняя часть автомобиля деформируется, а тело водителя перемещается на l = 0,7 м и останавливается. Определить среднее ускорение водителя во время этого столкновения. Выразить ответ в единицах, кратных ускорению свободного падения. g = 9.8 м/с2. (a = u20 /(2l); a = 14g) 42. Поезд длины l = 350 м начинает двигаться по прямому пути с постоянным ускорением а = 3,0´10-2 м/с2. Через t = 30 с после начала движения был включен прожектор локомотива (событие 1), а через τ = 60 с после этого — сигнальная лампа в хвосте поезда (событие 2). Найти расстояние между этими событиями в системах отсчета, связанных с поездом и Землей. Как и с какой постоянной скоростью u относительно Земли должна перемещаться некоторая K-система отсчета, чтобы оба события произошли в ней в одной точке? (u= (l /t) – a (t /2 + t)) 43. Машина едет по шоссе за грузовиком с той же скоростью. Между двойными шинами заднего колеса грузовика застрял камень. На каком расстоянии от грузовика должен ехать легковой автомобиль, чтобы камень, вырвавшийся из-под колеса грузовика, не попал в нее? ( 44. Точка движется по кривой с постоянным тангенциальным ускорением a t= 0,5 м/с2. Определить полное ускорение а точки на участке кривой с радиусом кривизны R = 3м; если точка движется на этом участке со скоростью u = 2м/с. (а =1,42м/с2) 45. Уравнение вращения колеса радиусом R = 0,5 м имеет вид j = At + Bt5, где А = 2 рад/с; В = 0,5 рад/с5. Определить полное ускорение в момент t =1 с точки, находящейся на ободе колеса. (a =11,3 м/с2) 46. Точка начинает движение по окружности радиусом R = 10 м. Пройденный ею путь зависит от времени по закону s = At + Bt3, где А = 8 м/с, В = 1м/с3. Определить скорость и полное ускорение точки b момент t= 2 с, (u = 20 м/с; а = 41,8 рад/с2) 47. По истечении времени t =2 с после начала равноускоренного вращения вектор ускорения точки, лежащей на ободе, составляет угол a = 60° с направлением линейной скорости этой точки. Найти угловое ускорение колеса. (s = 0,43 рад/с2) 48. Материальная точка начинает двигаться по окружности радиуса r = 0,1 м с постоянным касательным ускорением at = 0,004 м/с2. Через какой промежуток времени вектор ускорения
49. Материальная точка начинает двигаться по окружности радиусом r =12,5 см с постоянным тангенциальным ускорением aτ = 0,5 см/с2. Определите: 1)момент времени, при котором вектор ускорения a образует с вектором скорости v угол α = 45 0; 2) путь, пройденный за это время движущейся точкой. 50. Диск вращается вокруг неподвижной оси так, что зависимость угла поворота радиуса диска от времени задается уравнением φ = At2 (A =0,1рад/с2). Определите полное ускорение a точки на ободе диска к концу второй секунды после начала движения, если линейная скорость этой точки в этот момент равна 0,4 м/с. 51. За время tколесо поворачивается на угол j, зависящий от времени по закону j = 5,0t + 3,0t2 - 4,5t4, причем j измеряется в радианах, a t - в секундах. Определить: 1) среднюю скорость колеса; 2) среднее угловое ускорение за промежутки времени от t = 2,0 с до t = 3,0 с; 3) выражение для мгновенной угловой скорости w; 4) выражение для мгновенного углового ускорения e; 5) вычислить значения мгновенной угловой скорости и мгновенного углового ускорения в момент времени t - 3,0 с. (1) -280 рад/с; 2) -340 рад/с2; 3) 5,0 + 6,0t- 18t3; 4) 6 – 54t2; 5) -463 рад/с, -480 рад/с2) 52. Колесо диаметром 40см вращается с постоянным ускорением так, что за 3,6 с частота вращения возрастает от 80 до 300 об/мин. Вычислить: 1) угловое ускорение колеса; 2) радиальную и тангенциальную составляющие вектора линейного ускорения точки на ободе колеса через 2,0 с после начала ускоренного движения колеса. (1) 6,4 рад/с2; 2) 66 м/с2; 2,6 м/с2) 53. Два резиновых диска расположены рядом друг с другом так, что их края соприкасаются. Первый диск радиусом R1 = 3,0 см начинает вращаться с угловым ускорением e = 0,88 рад/с2 и заставляет вращаться второй диск радиусом R2 =5,0 см, причем второй диск вращается относительно первого диска без проскальзывания. Определить: 1) за какой промежуток времени второй диск достигает угловой скорости 33 об/мин, если в начальный момент он находился в покое; 2) угловое ускорение второго диска. (1)6,5 с; 2) 0,53 рад/с2) 54. Колеса автомобиля совершают 55 оборотов за промежуток времени, в течение которого скорость равномерно уменьшилась от 80 км/ч до 55 км/ч. Диаметр колеса равен 1,0 м. Определить: 1) чему было равно угловое ускорение колеса; 2) если автомобиль продолжает замедляться с тем же ускорением, то сколько времени ему понадобится до полной остановки. (1)-1,5 рад/с2; 2) 20 с) 55. Тело брошено со скоростью u0 = 10 м/с под углом a = 30° к горизонту. Найти радиус кривизны через t = 1 с. (R = 6,3м) 56. На большой горизонтальной поверхности закреплена маленькая пушка, которая выбрасывает снаряд со скоростью u0 = 50 м/с. На расстоянии l = 50 м от пушки находится вертикальная стена высотой h = 25 м. Поставлена задача — забросить снаряд как можно дальше за стену. Под каким углом а к горизонту следует стрелять и как далеко улетит снаряд за стену? (g = 10 м/с2, сопротивление воздуха не учитывать.) (a = 33°; s = 227 м) Динамика
57. Тело массой m движется в плоскости xy по закону x = A cos wt, y = B sin wt, где A, B, и – некоторые постоянные. Определите модуль силы, действующей на это тело. 58. Тело массой m = 2 кг движется прямолинейно по закону (F = 3,2 H.) 59. Тело массой m = 2 кг падает вертикально с ускорением a = 5 м/с2. Определите силу сопротивления при движении этого тела. (Fсопр = 9,62 Н.) 60. Снаряд массой m = 5 кг, вылетевший из орудия, в верхней точке траектории имеет скорость u = 300 м/с2. В этой точке он разорвался на два осколка, причем больший осколок массой m1 = 3 кг полетел в обратном направлении со скоростью u1 =100 м/с. Определите скорость u2 второго, меньшего, осколка. (u2 = 900 м/с) 61. Под действием какой силы при прямолинейном движении тела изменение его координаты со временем происходит по закону
62. Тело массой m = 70 кг движется под действием постоянной силы F = 63 Н. Определите, на каком пути s скорость этого тела возрастает в n = 3 раза по сравнению с моментом времени, когда скорость тела была равна u0 = 1,5 м/с. (s = 10 м) 63. Два тела m1= 0,1 кг и m2 = 0,5 кг связаны нерастяжимой нитью длиной l, перекинутой через блок радиуса R = 0,1 м. Определить координаты x1 и x2 этих тел через 5 секунд после начала движения, если x0 = 3,314 м (см. рис.)? Ускорение свободного падения g = 10 м/с2.
64. Простейшая машина Атвуда, применяемая для изучения законов равноускоренного движения, представляет собой два груза с не равными массами m1 и m2 (например m1 > m2), которые подвешены на легкой нити, перекинутой через неподвижный блок. Считая нить и блок невесомыми и пренебрегая трением в оси блока, определите: 1) ускорение грузов; 2) силу натяжения нити T; 3) силу, F действующую на ось блока 65. Пуля массой m = 15 г, летящая с горизонтальной скоростью u = 0,5 км/с, попадает в баллистический маятник М = 6 кг и застревает в нем. Определите высоту h, на которую поднимется маятник, откачнувшись после удара. (h = 7.9 см) 66. На спокойной воде пруда перпендикулярно берегу и носом к нему стоит лодка массой М и длиной L. На корме стоит человек массой m. На какое расстояние s удалится лодка от берега, если человек перейдет с кормы на нос лодки? Силами трения и сопротивления пренебречь. 67. Частица массой 10 г совершает гармонические колебания с периодом 2,0 с. Полная энергия колеблющейся частицы 0,10 мДж. Определить амплитуду колебаний и наибольшее значение возвращающей силы. (45 мм; 4,4 мН) 68. Определить угловую частоту колебаний груза массой 0,80 кг, закрепленного на двух пружинах между горизонтальными опорами. С одной стороны груза жёсткость пружины равна 1500 Н/м, с другой - 500 Н/м. (50 с-1) 69. Вычислить ускорение падающего груза а = 2h/t2, где h - высота, с которой падает тело, измерена линейкой (1 мм/дел.); t - время падения, измерено секундомером (0,2 с/дел.): h, см 87,4 87,5 87,3; t, с 7,8 8,0 7,8 7,6 7,8. 70. Определить максимальную кинетическую энергию материальной точки массой 2,0 г, совершающую гармонические колебания с амплитудой 4,0 см и частотой 5,0 Гц. (1,6 мДж) 71. Груз массой т подвешен на двух параллельных пружинах, жёсткости которых k1 и k2. Определить период колебаний груза. Массами пружин пренебречь.
72. Точка движется замедленно по окружности радиусом R так, что её тангенциальное и нормальное ускорения равны по модулю в каждый момент времени. В начальный момент скорость точки равна yo. Определить зависимость скорости точки и модуля полного ускорения от пройденного пути. (u = u0 exp(-s /К); а = (u02 /R)exp(-2s/R) 73. Тело массой 100 г совершает гармонические колебания с амплитудой 50,0 мм, периодом 10,0 мс и Нулевой начальной фазой. Определить частоту колебаний, угловую частоту, максимальные значения скорости и ускорения, энергию колебательной системы. (100 Гц; 628 с-1; 31,4 м/с;19,7 км/с2; 49,3 Дж) 74. Диск радиусом 24 см колеблется около горизонтальной оси, проходящей через середину одного из радиусов перпендикулярно к плоскости диска. Определить период колебаний. (1,2 с) 75. Материальная точка совершает колебания согласно уравнению х = 5 sin 2t, где х - смещение, см; t - время, с. Найти момент времени (ближайший к началу отсчета), в который потенциальная энергия точки равна 0,1 мДж, а возвращающая сила равна 5 мН. Определить фазу колебаний в этот момент времени. (0,5 с; 0,9 рад) 76. Колебательная система успевает совершить 100 колебаний за 100 с. За это же время амплитуда уменьшается в 2,72 раза. Найти коэффициент затухания колебаний и логарифмический декремент затухания. (0,0100 с-1; 0,0100) 77. Скорость автомобиля при экстренном торможении изменялась по закону u = 49 – 1,0 t2, где u- скорость, м/с; t - время, с. Определить время торможения и тормозной путь. (7,0 с и 0,23 км) 78. Точка участвует одновременно в двух колебаниях с одинаковым периодом и одинаковыми начальными фазами. Амплитуды колебаний равны 3 и 4 см. Найти амплитуду результирующего колебания, если 1) колебания совершаются в одном направлении; 2) колебания взаимно перпендикулярны. (7 см; 5 см) 79. Математический маятник длиной 50 см совершает свободные колебания в среде с коэффициентом затухания 0,90 с-1. Определить время, за которое амплитуда колебаний уменьшится в пять раз. (1,8 с) 80. Частица движется с постоянной по модулю скоростью v по параболической траектории у = k x2, где k – положительная постоянная. Определить ускорение частицы в точке х = 0, (а = 2kv2) 81. Брусок массой т находится на доске массой М, которая лежит на гладкой горизонтальной плоскости. Коэффициент трения между бруском и доской равен k. К доске приложили горизонтальную силу F, зависящую от времени по закону F = At, где А - постоянная. Найти момент времени t0, когда начнется движение бруска относительно доски.
82. Небольшое тело соскальзывает с вершины гладкой сферы радиусом R. Найти скорость тела в момент отрыва от поверхности сферы, если его начальная скорость пренебрежимо мала.
83. Водитель начинает тормозить на расстоянии 10 м от препятствия. Сила трения в тормозных колодках колес равна 17 кН. Какой может быть скорость машины массой 1500 кг, чтобы она остановилась перед препятствием? Потери энергии на трение колес о дорогу не учитывать. (u < 54 км/ч) 84. На краю неподвижной скамьи Жуковского диаметром 0,8 м и массой 6,0 кг стоит человек массой 60 кг. С какой угловой скоростью начнет вращаться скамья, если человек поймает летящий на него мяч массой 0,5 кг? Траектория мяча горизонтальна и проходит на расстоянии 0,4 м от оси скамьи. Скорость мяча 5 м/с. (0,1 рад/с) 85. По рельсам фуникулера, проложенным с уклоном a к горизонту, опускается вагон массой т. Скорость вагона на всём пути равна v, время торможения перед остановкой - t. Найти натяжение каната при торможении. Коэффициент трения между вагоном и рельсами равен k,
86. Автомобиль начинает движение с постоянным тангенциальным ускорением аt по горизонтальной дороге, описывая окружность радиусом R. Коэффициент трения между колесами машины и дорогой равен k. Какой путь s пройдет автомобиль без скольжения, если начальная скорость его была равна нулю?
87. Горизонтальная платформа массой 100 кг вращается вокруг вертикальной оси, проходящей через её центр, совершая 10 об/мин. Человек массой 60 кг стоит на краю платформы. С какой частотой начнет вращаться платформа, если человек перейдет от края: платформы к центру? Считать платформу однородным диском. (0,37 об/с) Работа и энергия 88. При выстреле из пружинного пистолета вертикально вверх пуля массой 20 г поднялась на высоту 5 м. Определить жесткость k пружины пистолета, если она была сжата на 10 см. Массой пружины пренебречь.
89. Комета массой т = 8,38 • 1011 кг сталкивается с Землей, имея относительно нее скорость u = 30 км/ с. 1) Найти энергию E взрыва и выразить ее в единицах тротилового эквивалента (т. е. указать количество тротила, выделяющего при взрыве ту же энергию). Энергия взрыва 1 кг тротила равна W == 4,2 МДж. 2) Оценить диаметр d образующегося при таком взрыве кратера. Обычно диаметр кратера пропорционален кубическому корню из энергии взрыва. Известно также, что взрыв водородной бомбы с тротиловым эквивалентом 1 Мт приводит к образованию кратера диаметром в 1 км. (1) E = 90 000 Мт; 2) d = 45 км) 90. Рассчитать полную работу А, совершаемую вертолетом массой М, который поднимается на высоту h с ускорением, направленным вверх, и равным 0,10g. (A = 1,1Mgh) 91. Вычислить работу, совершаемую на пути s = 12 м силой, равномерно возрастающей с пройденным расстоянием, если в начале пути сила F(0) = 10 Н, в конце пути F(s) = 46 H. (А = 336 Дж) 92. Камень брошен вверх под углом a = 60° к плоскости горизонта. Кинетическая энергия камня в начальный момент Т0 = 20 Дж. Определить кинетическую Т и потенциальную U энергии камня в высшей точке его траектории. (Т = 5Дж; U=15Дж) 93. Материальная точка массой m = 2 кг двигалась под действием некоторой силы согласно уравнению s = А + Bt + Ct2 + Dt3, где А= 10 м; В =- 2 м/с; С = 1 м/с2; D = -0,2 м/с3. Найти мощность, развиваемую при движении, в моменты времени t1 =2c и t2 = 5c. (N1 = 0,32 Вт; N2 = 56 Вт) 94. Ящик массой m1 = 20 кг соскальзывает по идеально гладкому лотку длиной l = 2 м на неподвижную тележку с песком и застревает в нем. Тележка с песком массой m2 = 80 кг может свободно (без трения) перемещаться по рельсам в горизонтальном направлении. Определить скорость v тележки с ящиком, если лоток наклонен под углом α = 30 0 к рельсам. 95. Конькобежец массой m1 = 60 кг, стоя на льду, бросил ядро массой m2 = 5 кг и вследствие отдачи покатился назад со скоростью u1 = 1 м/с. Определить работу A, совершаемую при бросании ядра. (A = 390Дж) 96. Тело массой m1 = 5 кг ударяется о неподвижное тело массой m2 = 2,5 кг. Кинетическая энергия этих тел после удара Т = 5 Дж. Считая удар центральным и неупругим, найти кинетическую энергию первого тела до удара. (T1 = 7,5Дж) 97. Масса одного автомобиля в 2 раза больше массы другого, а его кинетическая энергия равна половине кинетической энергии второго автомобиля. Когда оба автомобиля увеличили свою скорость на 3 м/с, их кинетическая энергия стала одинаковой. Каковы были начальные скорости каждого из автомобилей? (u1 = 2,12 м/с; u2 = 4,24 м/с) 98. Шар массой m испытывает лобовое соударение со вторым шаром (покоившимся до удара) и отлетает от него в противоположную первоначальному движению сторону со скоростью, равной одной трети начальной. Чему равна масса второго шара? (m1 = m2) 99. Покажите, что в общем случае при любом лобовом одномерном упругом столкновении двух тел скорости после него имеют следующие значения:
где u1, u2 - скорости тел до столкновения.
100. Два бильярдных шара с одинаковыми массами движутся под прямым углом друг к другу и сталкиваются в начале системы координат хОу. Первый шар двигался до этого со скоростью 3 м/с вверх вдоль оси Оу, а второй - вправо вдоль оси Ох со скоростью 4,5 м/с. После столкновения второй шар движется вдоль положительного направления оси Оу. В каком направлении движется после соударения первый шар и чему равны при этом скорости обоих шаров? ( 101. Метеор массой около 108 кг сталкивается с Землей (М = 6×1024 кг) при скорости около 15 м/с и застревает в толще Земли. 1) Какова скорость «отдачи», полученная Землей? 2) Какая доля кинетической энергии метеора перешла в кинетическую энергию Земли? 3) На какую величину изменилась кинетическая энергия Земли в результате этого столкновения? (1)2,5×10-16 м/с; 2) 1,7×10-17; 3)1,9×10-7 Дж) 102. В результате взрыва тело распадается на две части, масса одной из которых в полтора раза больше другой. Какую кинетическую энергию приобретает каждая часть, если в процессе взрыва выделилась энергия 4500 Дж? (1,8кДж;2,7кДж) 103. В результате полностью неупругого столкновения между двумя телами с одинаковыми массами и одинаковыми скоростями u до столкновения оба тела начинают двигаться со скоростью u/3. Чему был равен угол между направлениями их скоростей до столкновения? (141°) 104. Из орудия массой ml = 5•103кг вылетает снаряд массой т2 = 100кг. Кинетическая энергия снаряда при вылете Т2 = 7,5 МДж. Какую кинетическую энергию получает орудие? (Т = 150кДж) 105. Два неупругих шара массами ml = 2 кг и т2 = 3 кг движутся со скоростями u1 = 8 м/с и u2 = 4 м/с соответственно. Найти работу А деформации шаров в двух случаях: 1) меньший шар нагоняет больший; 2) шары движутся навстречу друг другу. (1) А = 9,6 Дж; 2) А = 86,4 Дж) 106. Под действием постоянной силы F вагонетка прошла путь s = 5 м и приобрела скорость u = 2 м/с. Определить работу А силы, если масса вагонетки т = 400 кг и коэффициент трения m = 0,01. (A = 996Дж) 107. Лыжник скатывается с холма с нулевой начальной скоростью и проезжает 30 м вниз по склону, составляющему 18° с горизонтом. 1) Чему равна скорость лыжника у подножия холма, если коэффициент трения равен m = 0,08? 2) Если у подножия холма имеется горизонтальная площадка, покрытая снегом с тем же коэффициентом трения, то на какое расстояние по ней укатится лыжник? Используйте энергетические соображения.
108. Тело массой т = 1 кг, брошенное с вышки в горизонтальном направлении со скоростью u = 20 м/с, через t = 3 с упало на землю. Определить кинетическую энергию Т, которую имело тело в момент удара о Землю. (Г=632Дж) 109. На ракете, находящейся на высоте 6400 км от Земли и удаляющейся от нее со скоростью 1850 м/с, запускаются двигатели, которые выбрасывают газы со скоростью 1200м/с (относительно ракеты). Каков должен быть расход газов (в килограммах в секунду), если масса ракеты к этому моменту достигла значения 25 т, чтобы получить ускорение 1,7 м/с2?
110. Сани, наполненные песком, скользят без трения под уклон 30°. Песок высыпается из отверстия со скоростью 2 кг/с. Если движение начинается из состояния покоя с полной массой 40 кг, то какое время понадобится на то, чтобы сани прошли расстояние 120 м по наклонной плоскости? (t =7 с) 111. Два груза массами т1 = 10 кг и m 2 = 15кг подвешены на нитях длиной l = 2 м так, что грузы соприкасаются между собой. Меньший груз был отклонен на угол a = 60° и выпущен. На какую высоту h поднимутся оба груза после удара? Удар грузов считать неупругим. (h = 16 см) 112. Пуля массой т = 10 г, летевшая со скоростью u = 600 м/с, попала в баллистический маятник массой М = 5 кг и застряла в нем. На какую высоту h, откачнувшись после удара, поднялся маятник? (h = 7,35 см) 113. Пуля массой 44 г попадает в деревянный брусок массой 15,4 кг на горизонтальной поверхности прямо напротив ствола оружия. Коэффициент трения между бруском и поверхностью m = 0,28. После застревания пули брусок, прежде чем остановиться, проходит расстояние 18м. Найти начальную скорость пули при вылете из ствола. (3,5 км/с) 114. Частица массой т, движущаяся со скоростью
|
||||
|
Последнее изменение этой страницы: 2016-04-26; просмотров: 1002; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.12.147.12 (0.013 с.) |

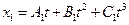 и
и  , где В1 = В2, С1 = -2 м/с2, С2 = 1 м/с2. Определите: 1) момент времени, для которого скорости этих точек будут равны; 2) ускорения а1 и а2 для этого момента.
, где В1 = В2, С1 = -2 м/с2, С2 = 1 м/с2. Определите: 1) момент времени, для которого скорости этих точек будут равны; 2) ускорения а1 и а2 для этого момента. , где
, где 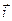 и
и  - орты осей x и y. Определите для момента времени t = 1 c: 1) модуль скорости; 2) модуль ускорения.
- орты осей x и y. Определите для момента времени t = 1 c: 1) модуль скорости; 2) модуль ускорения.
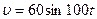 , где v - скорость, мм/с; t ~ время, с. Определить зависимость смещения от времени, а также максимальные значения скорости и ускорения тела.
, где v - скорость, мм/с; t ~ время, с. Определить зависимость смещения от времени, а также максимальные значения скорости и ускорения тела. и
и 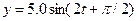 , где x и у - смещения, см; t - время, с. Найти уравнение траектории и скорость тела в момент времени 0,50 с.
, где x и у - смещения, см; t - время, с. Найти уравнение траектории и скорость тела в момент времени 0,50 с. ; 1,4 см/с)
; 1,4 см/с)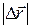 = 1118,0 км; a = 153,4°; 2)
= 1118,0 км; a = 153,4°; 2)  = 496,9 км; a = 153,4°; 3) ucp – 666.7 км/ч)
= 496,9 км; a = 153,4°; 3) ucp – 666.7 км/ч)
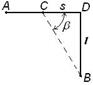
 на интервале от t0 = 0 с до t1 = 1 с и
на интервале от t0 = 0 с до t1 = 1 с и  на интервале от t1 = 1 с до t2 = 2 с.
на интервале от t1 = 1 с до t2 = 2 с.
 , где u0 – скорость автомобилей, h £ 1 м – высота камня в момент отрыва: s ³ 11 м (u0 = 36 км/ч); s ³ 40 м (u0 = 72 км/ч); s ³ 90 м (u0 = 108 км/ч)
, где u0 – скорость автомобилей, h £ 1 м – высота камня в момент отрыва: s ³ 11 м (u0 = 36 км/ч); s ³ 40 м (u0 = 72 км/ч); s ³ 90 м (u0 = 108 км/ч) образует с вектором скорости
образует с вектором скорости  угол a, равный: а) 60; б) 80о (см. рис. 2)? Какой путь пройдет за это время движущаяся точка? На какой угол повернется радиус-вектор, проведенный из центра окружности к движущейся точке, если в начальный момент времени он направлен вертикально вверх? Движение происходит по часовой стрелке.
угол a, равный: а) 60; б) 80о (см. рис. 2)? Какой путь пройдет за это время движущаяся точка? На какой угол повернется радиус-вектор, проведенный из центра окружности к движущейся точке, если в начальный момент времени он направлен вертикально вверх? Движение происходит по часовой стрелке.
 (С = 2 м/с2, D = 0,4 м/с2). Определите силу, действующую на тело в конце первой секунды движения.
(С = 2 м/с2, D = 0,4 м/с2). Определите силу, действующую на тело в конце первой секунды движения. ? Масса тела 2 кг.
? Масса тела 2 кг.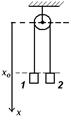

 )
)





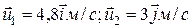 )
)

 вдоль оси <
вдоль оси < 


