
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Тема 1. Кинематика точки. Простейшие движения твёрдого тела.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Кинематика вращательного движения тв. тела. 1.1. Движущийся по дороге велосипедист крутит педали. Каково при этом движение педалей? Отметьте правильный ответ. +: Поступательное, -: Вращательное, -: Плоское. Ответ: Поступательное 1.2. Самолёт летит равномерно, горизонтально со скоростью 180 м/с. Лётчик стреляет из пулемёта вперёд, делая 600 выстрелов в минуту. На каком расстоянии s друг от друга будут ложиться пули на поверхность земли? s = … (м). Ответ: 18 1.3. У сенокосилки нож движется в направлении, перпендикулярном направлению движения косилки. Скорость косилки относительно луга 1,0 м/с, скорость ножа относительно косилки 1,5 м/с. Скорость ножа относительно луга равна (результат вычисления округлить до первого знака после запятой) … (м/с). Ответ: 1,8 1.4. Подъёмный кран поднимает груз вертикально вверх со скоростью 20 м/мин относительно тележки крана. Одновременно тележка движется горизонтально со скоростью 10 м/мин относительно земли. Модуль скорости груза относительно земли равен (результат вычисления округлить до первого знака после запятой) … (м/мин). Ответ: 22,4 1.5. За первые два часа велосипедист проехал 30 км, за следующие два часа 25 км и за последний час 15 км. Средняя скорость на всём пути равна … (км/час). Ответ: 14 1.6. Поезд движется на подъёме со скоростью 10 м/с и затем на спуске со скоростью 25 м/с. Длина спуска в 2 раза больше длины подъёма. Средняя скорость поезда на всём пути равна (результат вычисления округлить до целого числа) … (м/с) Ответ: 17 1.7. Весь путь автомобиль проехал со средней скоростью 80 км/ч. Средняя скорость на первой четверти пути равнялась 120 км/ч. Средняя скорость автомобиля на оставшейся части пути равна …(км/ч). Ответ: 72 1.8. Материальная точка M 1 движется по окружности радиуса R 1; матер. точка M 2 движется по окружности радиуса R 2, причём R 1 = 2ּ R 2. Линейные скорости этих точек равны (v 1 = v 2). Отношение их центростремительных ускорений a 1/ a 2 = … Ответ: 0,5 1.9. Материальная точка M 1 движется по окружности радиуса R 1; матер. точка M 2 движется по окружности радиуса R 2, причём R 1 = 2ּ R 2. Периоды их обращения равны (T 1 = T 2). Отношение их центростремительных ускорений a 1/ a 2 = … +: 2 1. v = … (м/с)
Ответ: 13 1.11. Точка равномерно движется по окружности со скоростью 10 м/с. Найти модуль изменения вектора скорости за одну четверть периода |Δ v 1/4|; половину периода |Δ v 1/2|; целый период |Δ v 1| (результат вычисления округлить до целого числа); |Δ v 1/4| = … (кгּм/с), |Δ v 1/2| = … (кгּм/с), |Δ v 1| = … (кгּм/с). Ответы: 14*20*0 1.12. За какое время t автомобиль, двигаясь с ускорением a = 0,4 (м/с2), увеличит свою скорость с 12 до 20 м/с? t = … (сек) Ответ: 20 1.13. При ударе кузнечного молота по заготовке ускорение при торможении молота было по модулю равно 200 м/с2. Сколько времени t длился удар, если начальная скорость молота была 10 м/с? (Числовой результат определить с точностью до второго знака после запятой) t = …(сек). Ответ: 0,05 1.14. Какую скорость приобретает ракета, движущаяся из состояния покоя с ускорением 60 м/с2, на пути 750 м? v = … (м/с) Ответ: 300 1. Отметьте правильный ответ. -: -: 1.16. Точка описывает фигуру Лиссажу согласно уравнениям x = 2ּ cos t, y = 4ּ cos 2 t. (x, y – в сантиметрах, t – в секундах). Определить модуль скорости точки, когда она находится на оси Oy. v = … (см/с) Ответ: 2
1.17. Двасамолёта одновременно вылетают из одного места по двум взаимно перпендикулярным направлениям. Один со скоростью v 1 = 300 км/час, другой со скоростью v 2 = 400 км/час. Как велико расстояние S между самолётами, когда первый из них пролетел путь S 1 = 900 км? S = … (км). Ответ: 1500 1.18. Копровая баба, ударив о сваю, движется затем вместе с ней в течение 0,02 сек. до остановки, причём свая углубляется в землю на 6 см. Определить начальную скорость v 0 движения сваи, считая его равнозамедленным. v 0 = …(м/с). Ответ: 6 1. v = … (м/с). Ответ: 5
Определить скорость точки в момент времени t 1 = 10 сек.. v 1 = … (м/с). Ответ: 0
1. v = … (м/с). Ответ: 3 1.
Отметьте правильный ответ.
+: 1), -: 2), -: 3), -: 4), -: 5), -: 6).
v = … а 0 ּt 1 (вместо многоточия подставить соответствующий множитель). Ответ: 0 1. Определить скорость точки в момент времени t = 10 с, если а 0 = 10 м/с2, а начальные условия движения точки – нулевые. v = … (м/с). Ответ: 40 1.25. Движение точки задано уравнениями x =5ּ cos (5 t 2), y =5ּ sin (5 t 2). (Значения координат x и y в см, время t в сек.) Определить значение пройденного пути s точкой за время t = 2 сек. от начала движения. s = … (см). Ответ: 100 1.26. Движение точки задано уравнениями x =3ּ sin (t), y =3ּ cos (t). (Значения координат x и y в см, время t в сек.) Определить значение пройденного пути s точкой за время t = 10 сек. от начала движения. s = … (см). Ответ: 30 1.27. Копровая баба падает с высоты 2,5 м, а для её поднятия на ту же высоту требуется втрое больше времени, чем на падение. Сколько ударов n в минуту она сделает, если считать, что свободное падение копровой бабы совершается с ускорением g = 9,8 м/с2? n = … (мин – 1) Ответ: 21 1.28. Пловец, спрыгнув с пятиметровой вышки, погрузился в воду на глубину 2 м. Ускорение свободного падения принять равным 10 м/с2. Сколько времени длилось погружение пловца в воду, и с каким ускорением он двигался в воде? Время погружения в воде … (сек), Модуль ускорения при движении в воде … (м/с2). Ответы: 0,4*25 1.29. При увеличении радиуса круговой орбиты искусственного спутника Земли в 4 раза период его обращения увеличивается в 8 раз. Во сколько раз изменяется скорость движения спутника по орбите? v 2 / v 1 = … Ответ: 0,5 1.30. Тело свободно падает с высоты 80 м. Каково его перемещение s в последнюю секунду падения? Ускорение свободного падения принять равным 10 м/с2. s = … (м) Ответ: 35
1.31. Поезд движется равнозамедленно по дуге окружности радиуса R = 800 м и проходит путь s = 800 м, имея начальную со скоростью v 0 = 54 км/час и конечную скорость v =18 км/час. Определить полное ускорение поезда a в начале дуги. (Результат вычисления округлить до второго знака после запятой.) a = …(м/с2). Ответ: 0,31 1.32. Поезд, имея начальную скорость 54 км/час, прошёл 600 м в первые 30 сек. Считая движение поезда равнопеременным, определить полное ускорение поезда a в конце 30-й секунды, если рассматриваемое движение поезда происходит на закруглении радиуса R = 1 км. (Результат вычисления округлить до второго знака после запятой.) a = …(м/с2). Ответ: 0,71 1.33. При отходе от станции скорость поезда возрастает равномерно и достигает величины 72 км/час через 3 мин после отхода; путь расположен на закруглении радиуса 800 м. Определить полное ускорение поезда a через 2 мин после момента отхода от станции. (Результат вычисления округлить до второго знака после запятой.) a = …(м/с2). Ответ: 0,25
1.34. По наклонной доске пустили катиться снизу вверх шарик. На расстоянии 30 см от начала пути шарик побывал дважды: через 1 сек и через 2 сек от начала движения. Определить начальную скорость v 0 шарика. v 0 = … (см/с). Ответ: 45 1.35. Точка движется по окружности радиуса R = 0,5 м по закону s = t 2 – t (s – в метрах, t – в секундах). Определить момент времени t 1 > 0, когда касательное ускорение точки равно её нормальному ускорению; t 1 = … (сек). Ответ: 1 1.36. Движение точки задано уравнениями x =3ּ cos (πּt/ 3), y =3ּ sin (πּt/ 3). (Значения координат x и y в метрах, время t в сек.) Определить касательное a τ и нормальное a n ускорения точки. (Результат вычисления округлить до первого знака после запятой.) a τ = … (м/с2), a n = … (м/с2). Ответы: 0*3,3 1.37. Камень, брошенный с крыши дома горизонтально с начальной скоростью v 0 = 15 м/с, упал на землю под углом α = 60о к горизонту. Какова высота h дома? g = 9,8 м/с2. (Результат вычисления округлить до первого знака после запятой.) h = … (м). Ответ: 34,4 1.38. Тело брошено горизонтально. Через время t = 3 сек. после броска направления полной скорости v и полного ускорения a составили угол β = 45о. Найти полную скорость v тела в этот момент. Ускорение свободного падения g = 9,8 м/с2. (Результат вычисления округлить до первого знака после запятой.) землю. v = … (м/с). Ответ: 41,6 1. Отметьте правильный ответ. -: tABC = t ADC, +: tABC > t ADC, -: tABC < t ADC.
1.40. Две матер. точки движутся по окружностям одинакового радиуса с одинаковыми по модулю ускорениями. Ускорение первой точки направлено под углом к касательной, второй – по радиусу. У какой из этих точек модуль скорости больше? Отметьте правильный ответ. -: скорости точек равны; -: скорость первой точки больше; +: скорость второй точки больше. 1.41. Два тела брошены одновременно из одной точки – одно вверх, другое вниз, оба с начальной скоростью v 0 = 30 м/с под углом α = 60о к вертикали. Найти разность уровней (y 1 – y 2), на которых будут находиться тела спустя время t = 2 сек. (y 1 – y 2) = … (м). Ответ: 60 1.42. Какую начальную скорость v 0 имел снаряд, вылетевший из пушки под углом α = 30о к горизонту, если он пролете расстояние s = 17 300 м? Известно, что сопротивление воздуха уменьшило дальность полёта в 4 раза. (Результат вычисления округлить до целого числа.) v 0 = … (м/с). Ответ: 885 1.43. Локомотив находился на расстоянии L = 400 м от светофора и имел скорость 72 км/час, когда началось торможение. Определите расстояние L 1 локомотива относительно светофора через 1 минуту после начала торможения, если он двигался с отрицательным ускорением (торможение), равным по величине а = 0,5 м/с2. L 1= … (м). Ответ: 0 1.44. Камень падает в шахту без начальной скорости. Звук от удара камня о дно шахты слышен через 6,5 сек. от момента начала его падения. Скорость звука равна 330 м/с. Определить глубину h шахты. Ускорение свободного падения принять равным g = 9,8 м/с2. (Результат вычисления округлить до целого числа.) h … (м). Ответ: 175 1.45. Круглая пила имеет диаметр 600 мм. На ось пилы насажен шкив диаметром 300 мм, который ремённой передачей приводится во вращение от шкива диаметром 120 мм, насаженного на вал двигателя. Какова частота вращения (в об/мин.) ротора двигателя, если скорость зубьев пилы равна 15 м/с? n = …(об/мин) (результат округлить до целого числа). Ответ: 1194
n 4 = … (об/мин) (результат округлить до целого числа). Ответ: 60 1.47. Какое расстояние пройдёт велосипедист при 60 оборотах педалей, если диаметр колеса 70 см, ведущая зубчатка имеет 48 зубцов, а ведомая – 18 зубцов? s = …(метров) (результат округлить до целого числа). Ответ: 352 1. С какой скоростью движется груз, если верёвку тянуть со скоростью v? v груз = Qּv (определить Q с точностью до второго знака после запятой включительно) Ответ: 0,25
1. Определить ускорение точек обода диска. а = …(м/с2) Ответ: 8
1.50. Колесо 1 зубчатой передачи вращается по закону φ 1 = 2ּ t (φ 1 – в радианах, t – в секундах) и приводит в движение колесо 2. Радиусы колёс R 1 = 0,1 м, R 2 = 0,05 м. Найти ускорение точек обода второго колеса; а 2 = … (м/с2). Ответ: 0,8 1.51. В механической передаче движение от колеса 1 ω 3 = … (рад/с). Ответ: 8 1. ω 3 = …(рад/с). Ответ: 12
1. x = t 2 – t (х – расстояние груза от места схода нити с поверхности вала в метрах, t – в секундах), приводит в движение ремённую передачу. Найти угловое ускорение шкива 2, если радиусы шкивов R 1 = 0,5 м; R 2 = 1,0 м. ε 2 = … (рад/с2). Ответ: 2
x = t 2 – t (х – расстояние груза от места схода нити с поверхности вала в метрах, t – в секундах), приводит в движение ремённую передачу. Радиусы шкивов R 1 = 0,5 м; R 2 = 1,0 м. Найти ускорение точки М обода шкива 2 в момент времени t = 1 сек. a = …(м/с2) (результат округлить до второго знака после запятой включительно). Ответ: 2,24
1. v 6 = …(м/с). (результат округлить до первого знака после запятой включительно). Ответ: 0,6
Ответ: 0,05 1.57. В механизме домкрата при вращении рукоятки А начинают вращаться шестерни 1, 2, 3, 4 и 5, которые приводят в движение зубчатую рейку В домкрата. Определить скорость рейки, если рукоятка А вращается с угловой скорость ω 1 = π рад/с. Числа зубцов шестерён z 1 = 6, z 2 = 24, z 3 = 8, z 4 = 32; радиус пятой шестерни r 5 = 4 см. v B = …(мм/с) (результат округлить до целого числа). Ответ: 8 1.58. ε2 = … (рад/с2). Ответ: 2 1.59. Отметьте правильный ответ. На рисунке изображена система зубчатых колёс (R1 = R4, R2 = R3, R1 + 2R5 + R4 = R2 + R3). Могут ли вращаться зубчатые колёса изображённого механизма? -: Да; +: Нет 1.
Ответ: 90
61. Отметьте правильный ответ. На рисунке изображена система зубчатых колёс (R1 = R6 = R5 = R4, R2 = = R3, R1+ 2R6 + 2R5 + R4 = R2 + R3). Могут ли вращаться зубчатые колёса изображённого механизма? +: Да; -: Нет 1.62. ω3 = … (рад/с). Ответ: 24
Отметьте правильный ответ: +: к точке О -: к точке А -: к точке В -: к точке С
Отметьте правильный ответ: -: к точке О -: к точке А -: к точке В +: к точке С 1.65. Отметьте правильный ответ: -: к точке О -: к точке А +: к точке В
1.66. Диск равномерно вращается с угловой скоростью ω (см. рис.). Вдоль хорды диска движется точка М с относительной скоростью vr. Определить направление ускорения Кориолиса в данный момент времени. Отметьте правильный ответ: -: к точке О -: к точке А +: к точке В -: к точке С 1.67. Подвижный подъёмный кран перемещается по горизонтальным рельсам O 1 D согласно уравнению s = 2 + t – t 2 (см). Стрела крана OK перпендикулярна рельсам; по стрела движется тележка А согласно уравнению x = 1 – 2ּ t (см). Груз В движется вертикально с помощью лебёдки, установленной на тележке, по закону у = 3ּ t 2 + 1 (см).
Варианты ответов:
-: +: -: -:
Определить ускорение стержня. а ст. = … (мм/с2) (результат вычисления округлить до первого знака после запятой включительно). Ответ: 11,5 I: 1.69.
Определить относительную скорость ползуна А (относительно кулисы KLM) в тот момент, когда угол φ = 45о (результат вычисления округлить до первого знака после запятой включительно); v отн = … (см/с). Ответ: 42,4 1.70. Определить скорость кулисы KLM (v 1) в тот момент, когда угол φ = 45о (результат вычисления округлить до первого знака после запятой включительно); v 1 = … (см/с). Ответ: 42,4
Определить относительную скорость ползуна А (относительно кулисы KLM) в тот момент, когда угол φ = 30о (результат вычисления округлить до до целого числа); v отн = … (см/с). Ответ: 52 1.72.
Определить скорость о кулисы KLM (v 1) в тот момент, когда угол φ = 30о); v 1 = … (см/с). Ответ: 30
Определить относительную скорость ползуна А (относительно кулисы KLM) в тот момент, когда угол φ = 60о (результат вычисления округлить до целого числа); v отн = … (см/с). Ответ: 30
1.74. В кривошипно-кулисном механизме кривошип ОА = 10 см вращается с угловой скоростью ω = 6 с –1. Определить скорость кулисы KLM (v 1) в тот момент, когда угол φ = 60о (результат вычисления округлить до целого числа); v 1= … (см/с). Ответ: 52 1.75. Определить скорость кулисы KLM (v 1) в тот момент, когда угол φ = 90о (результат вычисления округлить до целого числа); v 1= … (см/с). Ответ: 60 1.76. Определить относительную скорость ползуна А (относительно кулисы KLM) в тот момент, когда угол φ = 90о; v отн = … (см/с). Ответ: 0
1.77. Прямолинейный стержень вращается в горизонтальной плоскости вокруг вертикальной оси. Вдоль стержня движется точка с относительной скоростью Vr. Кориолисово ускорение направлено НЕВЕРНО на рисунке… ВАРИАНТЫ ОТВЕТОВ: 1)2) 3) 4)
-: 1), +: 2), -: 3), -: 4). 1.78. y = 4ּ(2ּ t + t 2 ) (см). (см). Определить абсолютное ускорение груза В; а абс = …(см/с2)
Определить абсолютное ускорение груза В (результат вычисления округлить до первого знака после запятой включительно); а абс = …(см/с2)
|
||||
|
Последнее изменение этой страницы: 2016-04-07; просмотров: 900; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.189.182.15 (0.013 с.) |

 10. На рис. представлен график зависимости ускорения точки от времени a (t). Вычислить скорость точки v через t = 6 сек от начала движения;
10. На рис. представлен график зависимости ускорения точки от времени a (t). Вычислить скорость точки v через t = 6 сек от начала движения; 15. Ползуны А и В двухползунного механизма движутся соответственно по осям Ох и Оу. Написать уравнение траектории точки М звена АВ механизма, если АМ = a, МВ = b.
15. Ползуны А и В двухползунного механизма движутся соответственно по осям Ох и Оу. Написать уравнение траектории точки М звена АВ механизма, если АМ = a, МВ = b. , +:
, +:  , -:
, -:  ,
, , -:
, -:  , -:.
, -:. 
 19. Матер. точка массы движется вдоль горизонтальной оси Ox. График изменения ускорения аx точки с течением времени представлен на рис. Принимая, что при t = 0 x = x 0 = 0 и
19. Матер. точка массы движется вдоль горизонтальной оси Ox. График изменения ускорения аx точки с течением времени представлен на рис. Принимая, что при t = 0 x = x 0 = 0 и 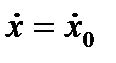 = 2 м/с, определить скорость точки после истечения времени t = 5 сек. от начала движения, если а 1 = 12 м/с2, а 2 = 4,5 м/с2.
= 2 м/с, определить скорость точки после истечения времени t = 5 сек. от начала движения, если а 1 = 12 м/с2, а 2 = 4,5 м/с2. 1.20. Матер. точка движется вдоль горизонтальной оси Ox. График изменения ускорения аx с течением времени представлен на рис., где а 0 = 2 м/с2. Начальная скорость матер. точки равна 6 м/с.
1.20. Матер. точка движется вдоль горизонтальной оси Ox. График изменения ускорения аx с течением времени представлен на рис., где а 0 = 2 м/с2. Начальная скорость матер. точки равна 6 м/с. 21. Матер. точка движется вдоль горизонтальной оси Ox. График изменения ускорения аx с течением времени представлен на рисунке. Принимая, что при t 0 = 0 x = x 0 = 0 и
21. Матер. точка движется вдоль горизонтальной оси Ox. График изменения ускорения аx с течением времени представлен на рисунке. Принимая, что при t 0 = 0 x = x 0 = 0 и  , определить скорость точки в момент времени t = 10 сек от начала движения, если а 1 = 12 (м/с2), а а 2 = 4,5 (м/с2).
, определить скорость точки в момент времени t = 10 сек от начала движения, если а 1 = 12 (м/с2), а а 2 = 4,5 (м/с2). 22. График зависимости от времени ускорения а (t) матер. точки имеет вид, представленный на рис.; начальная скорость точки равна нулю. Определить график зависимости от времени скорости точки.
22. График зависимости от времени ускорения а (t) матер. точки имеет вид, представленный на рис.; начальная скорость точки равна нулю. Определить график зависимости от времени скорости точки.
 1.23. Матер. точка движется вдоль горизонтальной оси Ox. График изменения ускорения аx с течением времени представлен на рисунке. Принимая, что при t 0 = 0 x = x 0 = 0 и
1.23. Матер. точка движется вдоль горизонтальной оси Ox. График изменения ускорения аx с течением времени представлен на рисунке. Принимая, что при t 0 = 0 x = x 0 = 0 и  24. Матер. точка движется вдоль горизонтальной оси Ox. График изменения ускорения аx с течением времени представлен на рисунке.
24. Матер. точка движется вдоль горизонтальной оси Ox. График изменения ускорения аx с течением времени представлен на рисунке. 39. Небольшой шарик движется без трения один раз по желобу АВС (см. рис.), а другой раз по желобу АDС. Части желоба АD и ВС вертикальны, а углы АВС и АDС закруглены. Изобразить графически для обоих случаев зависимость скорости v шарика от времени t, если АВ = ВС = АD = DС = h. Скорость шарика в точке А равна нулю. По какому пути (АВС или АDС) шарик скорее попадёт из точки А в точку С?
39. Небольшой шарик движется без трения один раз по желобу АВС (см. рис.), а другой раз по желобу АDС. Части желоба АD и ВС вертикальны, а углы АВС и АDС закруглены. Изобразить графически для обоих случаев зависимость скорости v шарика от времени t, если АВ = ВС = АD = DС = h. Скорость шарика в точке А равна нулю. По какому пути (АВС или АDС) шарик скорее попадёт из точки А в точку С? 1.46. Движение от шкива I (см. рис.) к шкиву IV передаётся при помощи двух ремённых передач. Найти частоту вращения (об/мин) шкива IV, если шкив I делает 1200 об/мин., а радиусы шкивов r 1 = 8 см; r 2 = 32 см; r 3 = 11 см; r 4 = 55 см. Шкивы II и III жёстко укреплены на одном валу.
1.46. Движение от шкива I (см. рис.) к шкиву IV передаётся при помощи двух ремённых передач. Найти частоту вращения (об/мин) шкива IV, если шкив I делает 1200 об/мин., а радиусы шкивов r 1 = 8 см; r 2 = 32 см; r 3 = 11 см; r 4 = 55 см. Шкивы II и III жёстко укреплены на одном валу. 48. Груз Р подвешен с помощью трёх блоков 1, 2, 3, причем оси блоков 1 и 3 установлены на подвижной раме с грузом, ось блока 2 неподвижна.
48. Груз Р подвешен с помощью трёх блоков 1, 2, 3, причем оси блоков 1 и 3 установлены на подвижной раме с грузом, ось блока 2 неподвижна. 49. Диск радиуса R = 0,5 м приводится в движение грузом Р, который опускается вниз по наклонной плоскости согласно закону x = 2ּ t (х – расстояние от груза до места схода верёвки с диска в метрах, t – в секундах).
49. Диск радиуса R = 0,5 м приводится в движение грузом Р, который опускается вниз по наклонной плоскости согласно закону x = 2ּ t (х – расстояние от груза до места схода верёвки с диска в метрах, t – в секундах). передаётся шкиву 2, а от него – бесконечным ремнём шкиву 3. Радиусы колёс R 1 = 0,2 м; R 2 = 0,5 м; R 3 = 0,25 м, угловая скорость колеса 1 ω 1 = 10 рад/с. Пренебрегая скольжением ремня по шкивам, определить угловую скорость ω 3 шкива 3.
передаётся шкиву 2, а от него – бесконечным ремнём шкиву 3. Радиусы колёс R 1 = 0,2 м; R 2 = 0,5 м; R 3 = 0,25 м, угловая скорость колеса 1 ω 1 = 10 рад/с. Пренебрегая скольжением ремня по шкивам, определить угловую скорость ω 3 шкива 3.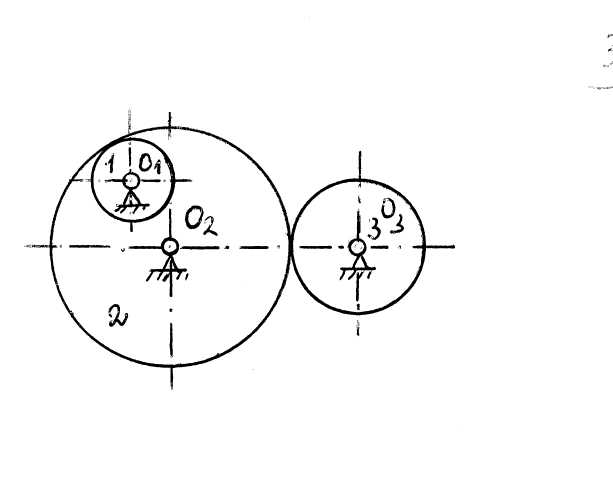 52. В механической передаче движение от колеса 1 передаётся колесу 3. Определить угловую скорость ω 3 колеса 3, если угловая скорость колеса 1 ω 1 = 15 рад/с и числа зубьев колёс z 1 = 20, z 2 = 50, z 3 = 25.
52. В механической передаче движение от колеса 1 передаётся колесу 3. Определить угловую скорость ω 3 колеса 3, если угловая скорость колеса 1 ω 1 = 15 рад/с и числа зубьев колёс z 1 = 20, z 2 = 50, z 3 = 25.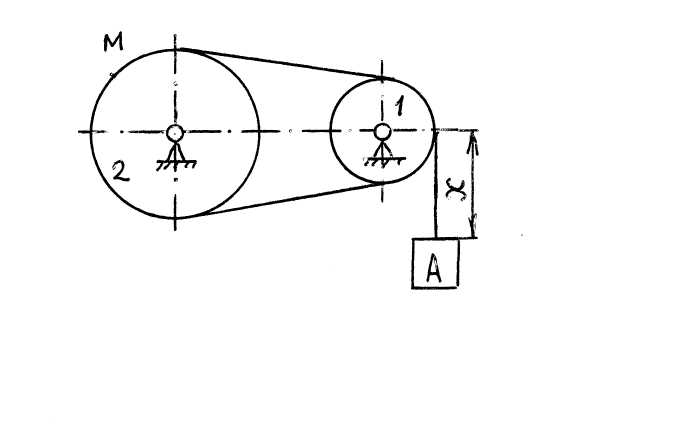 53. Груз А, опускаясь согласно закону
53. Груз А, опускаясь согласно закону 55. В механизме движение от шестерни 1 передаётся шестерням 2, 3, 4, 5 и зубчатой рейке АВ. Определить модуль и направление скорости рейки, если ω 1 = 2 рад/с и радиусы зубчатых колёс R 1 = R 2 = R 3 = R 5 = 0,2 м, R 4 = 0,3 м.
55. В механизме движение от шестерни 1 передаётся шестерням 2, 3, 4, 5 и зубчатой рейке АВ. Определить модуль и направление скорости рейки, если ω 1 = 2 рад/с и радиусы зубчатых колёс R 1 = R 2 = R 3 = R 5 = 0,2 м, R 4 = 0,3 м. 1.56. Механизм, состоящий из барабана 6 и зубчатой передачи, приводится в движение колесом 1. Определить модуль и направление скорости
1.56. Механизм, состоящий из барабана 6 и зубчатой передачи, приводится в движение колесом 1. Определить модуль и направление скорости  груза Р, если ω 1 = 4,5 рад/с и радиусы колёс и барабана равны R 1 = R 6 = 0,1 м; R 2 = R 3 = 0,3 м, R 4 = 0,15 м; R 5 = 0,45 м. Колесо 4 жёстко соединено с колесом 3, колесо 5 – с барабаном 6.
груза Р, если ω 1 = 4,5 рад/с и радиусы колёс и барабана равны R 1 = R 6 = 0,1 м; R 2 = R 3 = 0,3 м, R 4 = 0,15 м; R 5 = 0,45 м. Колесо 4 жёстко соединено с колесом 3, колесо 5 – с барабаном 6. v = … (м/с) (результат округлить до второго знака после запятой включительно).
v = … (м/с) (результат округлить до второго знака после запятой включительно). Радиусы 1-й и 2-й шестерни соответственно равны R 1 = 120 (мм) и R 2 =180 (мм); угловое ускорение 1-й шестерни ε1 = 3 (рад/сек2). Определить угловое ускорение 2-й шестерни.
Радиусы 1-й и 2-й шестерни соответственно равны R 1 = 120 (мм) и R 2 =180 (мм); угловое ускорение 1-й шестерни ε1 = 3 (рад/сек2). Определить угловое ускорение 2-й шестерни. 60. Определить скорость (см/с) тела 4. Значение угловой скорости диска 1 ω 1 = 15 рад/с; радиусы дисков: R 1 = R 3 = 2 R 2 = 60 (мм). V 4 = … (см/с).
60. Определить скорость (см/с) тела 4. Значение угловой скорости диска 1 ω 1 = 15 рад/с; радиусы дисков: R 1 = R 3 = 2 R 2 = 60 (мм). V 4 = … (см/с).
 Определить угловую скорость диска 3. Радиусы дисков 1 и 3: R 1 = 30 мм, R 3 = 40 мм; радиусы двойного диска 2: r 2 = 36 мм, R 2 = 45 мм. Угловая скорость диска 1: ω1 = 40 рад/с;
Определить угловую скорость диска 3. Радиусы дисков 1 и 3: R 1 = 30 мм, R 3 = 40 мм; радиусы двойного диска 2: r 2 = 36 мм, R 2 = 45 мм. Угловая скорость диска 1: ω1 = 40 рад/с; 1.63. Диск равномерно катится по горизонтальной прямой без скольжения, скорость его центра vO (см. рис.). Вдоль хорды диска движется точка М с относительной скоростью vr. Определить направление ускорения Кориолиса в данный момент времени.
1.63. Диск равномерно катится по горизонтальной прямой без скольжения, скорость его центра vO (см. рис.). Вдоль хорды диска движется точка М с относительной скоростью vr. Определить направление ускорения Кориолиса в данный момент времени. 1.64. Диск равномерно катится по горизонтальной прямой без скольжения, скорость его центра vO (см. рис.). Вдоль диаметра диска движется точка М с относительной скоростью vr. Определить направление ускорения Кориолиса в данный момент времени.
1.64. Диск равномерно катится по горизонтальной прямой без скольжения, скорость его центра vO (см. рис.). Вдоль диаметра диска движется точка М с относительной скоростью vr. Определить направление ускорения Кориолиса в данный момент времени.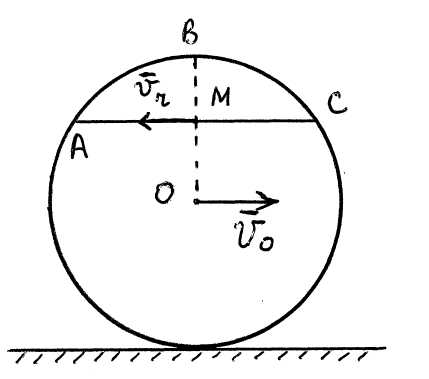 Диск равномерно катится по горизонтальной прямой без скольжения, скорость его центра vO (см. рис.). Вдоль хорды диска движется точка М с относительной скоростью vr. Определить направление ускорения Кориолиса в данный момент времени.
Диск равномерно катится по горизонтальной прямой без скольжения, скорость его центра vO (см. рис.). Вдоль хорды диска движется точка М с относительной скоростью vr. Определить направление ускорения Кориолиса в данный момент времени. -: к точке С
-: к точке С Абсолютное ускорение груза В равно …
Абсолютное ускорение груза В равно …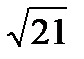




 1.68. Стержень скользит в вертикальных направляющих, опираясь нижним концом на гладкую наклонную поверхность треугольной призмы. Призма движется по горизонтали вправо с постоянным ускорением а 0 = 20 мм/ с2.
1.68. Стержень скользит в вертикальных направляющих, опираясь нижним концом на гладкую наклонную поверхность треугольной призмы. Призма движется по горизонтали вправо с постоянным ускорением а 0 = 20 мм/ с2. S: В кривошипно-кулисном механизме кривошип ОА = 10 см вращается с угловой скоростью ω = 6 с –1 .
S: В кривошипно-кулисном механизме кривошип ОА = 10 см вращается с угловой скоростью ω = 6 с –1 .
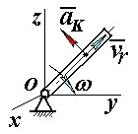

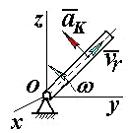
 Подвижный подъемный кран перемещается по горизонтальным рельсам O 1 D согласно уравнению s = 24ּ t – 5ּ t 2 (см). Стрела крана ОК параллельна рельсам, по стреле движется тележка А согласно уравнению x = 2ּ t 2 +3ּ t (см). Груз В движется вертикально с помощью лебедки, установленной на тележке, по закону
Подвижный подъемный кран перемещается по горизонтальным рельсам O 1 D согласно уравнению s = 24ּ t – 5ּ t 2 (см). Стрела крана ОК параллельна рельсам, по стреле движется тележка А согласно уравнению x = 2ּ t 2 +3ּ t (см). Груз В движется вертикально с помощью лебедки, установленной на тележке, по закону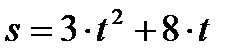 (см). Стрела крана ОК параллельна рельсам, по стреле движется тележка А согласно уравнению
(см). Стрела крана ОК параллельна рельсам, по стреле движется тележка А согласно уравнению  (см). Груз В движется вертикально с помощью лебедки, установленной на тележке, по закону
(см). Груз В движется вертикально с помощью лебедки, установленной на тележке, по закону  (см).
(см).


