
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Тема 7. Общие теоремы динамики (теорема об изменении количества движения; теорема об изменении кинетической энергии; вычисление работы; потенциальное силовое поле. Работа потенциальной силы).Содержание книги
Поиск на нашем сайте
Колебательное движение 7.1. Пружину с жёсткостью 140 Н/м сжали до длины 0,1 м и отпустили. Работа силы упругости при восстановлении пружины равно … Дж, если длина недеформированной пружины равна 0,2 м. Ответ: 0,7
Ответ: – 100
1) Ответы: 9*3 7.4. Определить: 1) работу силы тяжести А (Р) на перемещении груза М1М2; 2) какую минимальную скорость v 1 необходимо сообщить грузу, чтобы он достиг положения М2. (Начальный угол наклона стержня 30о)
7.5. Матер. точка массы m = 2 кг перемещается в вертикальной плоскости Оху. Определить работу А ОМ (Дж) силы тяжести Р = mּg при перемещении матер. точки по дуге OM полуокружности радиуса R = 10 м (см. рис.). Ускорение свободного падения принять равным g = 9,8 м/с2. Результат вычисления округлить до ближайшего целого числа. А ОМ = … (Дж) Ответ: – 392
Ответ: – 196 7.7. А 12 = … (Дж). Ответ: 6,4
А 12 = … (Дж). Ответ: – 10
А 12 = … (Дж). Ответ: 1 7.10. Матер. точка массы m движется по окружности радиуса r в поле центральной силы. Сила притяжения, убывающая обратно пропорционально квадрату расстояния, по модулю равна F (r) = Ответ: 2
7.11. Матер. точка массы m движется по окружности радиуса r в поле центральной силы притяжения. Сила притяжения по модулю равна F (r) = c ּ r, где c = const. (Центр окружности совпадает с силовым центром.) Определить значение скорости v точки при следующих числовых данных параметров: m = 0,25 (кг), c = 100 (Н/м) и r = 0,2 (м). v = … (м/с). Ответ: 4 7.12. Матер. точка массы m движется по окружности радиуса r под действием центральной силы притяжения Ответ: 2.
Ответ: 90
Ответ: – 90 7.15.
7.16. Искусственный спутник Земли движется по круговой орбите на высоте от поверхности Земли h, равной половине радиуса Земли (h = 0,5ּ R). Первая космическая скорость равна v косм1 = 7910 (м/с). Определить скорость v (м/с) спутника на обозначенной орбите. v = … (м/с). Ответ: 6459
Вычислить работу силы тяжести при этом повороте. Массой штанги пренебречь. Ускорение свободного падения принять равным g = 9,8 м/с2. А = … (Дж). (Результат вычисления округлить до первого знака после запятой включительно.) Ответ: 3,9
Вычислить работу силы тяжести при этом повороте. Массой штанги пренебречь. Ускорение свободного падения принять равным g = 9,8 м/с2. А = … (Дж). Ответ: 0
Проекция силы упругости пружины равна Fx = – cּx – b ּ x 3, где x – удлинение пружины; параметры c и b имеют следующие значения: c = 1000 Н/м, b = 4 Н/м3. Вычислить работу упругой силы пружины при перемещении груза на расстояние s = 1 м. А = … (Дж) Ответ: – 501 7.20 На двух одинаковых лёгких спиральных пружинках подвешены две гири, отношение масс которых m 1/ m 2 = 3. Гири получили толчки в вертикальном направлении и колеблются так, что амплитуда колебаний первого груза А 1 в 2 раза больше амплитуды колебаний А 2 второго груза. Как относится энергии их колебаний Е 1/ Е 2 ? Е 1/ Е 2 = … Ответ: 4 7.21. Дифференциальное уравнение движения материальной точки имеет вид 4ּ d 2 x/dt 2 + 12ּ dx/dt + c ּ x = 0. Определить максимальное значение коэффициента жёсткости с пружины, при котором движение будет апериодическим; с = … Отметьте правильный ответ. Ответ: 9 7.22. Дифференциальное уравнение движения материальной точки имеет вид d 2 x/dt 2+100ּ x = 15ּ sin 5 ּt. Определить амплитуду вынужденных колебаний А вынужд; (результат вычисления округлить с точностью до первого знака после запятой); А вынужд = …. Ответ: 0,2
7.23. Тело массой m = 0,1 кг движется прямолинейно по закону x = 2ּ sin (5 ּt) (м) под действием силы F. Определить наибольшее значение этой силы; | F | = …(H). Ответ: 5
7.24. Дифференциальное уравнение движения материальной точки имеет вид 2ּ d 2 x/dt 2 + b ּ dx/dt + 2ּ x = 0. Определить минимальное значение b min точки, при котором движение будет апериодическим: b min = … Ответ: 4 7.25. Дифференциальное уравнение движения материальной точки имеет вид d 2 x/dt 2+ 6ּ dx/dt + 25ּ x = 0. Определить условный период Т затухающих колебаний. Т = … (сек). Ответ: 2 π ּ0,25 7.26. Дифференциальное уравнение движения материальной точки имеет вид m ּ d 2 x/dt 2+2ּ dx/dt +5ּ x = 0. Определить максимальное значение массы m max точки, при котором движение будет апериодическим: m max = … (Результат вычисления определить с точностью до первого знака после запятой); Ответ: 0,2 7.27. Дифференциальное уравнение движения материальной точки имеет вид d 2 x/dt 2+8ּ dx/dt +25ּ x = 0. Определить, каким будет движение: равномерным, равноускоренным, колебательным или апериодическим. Отметьте правильный ответ. -: Равномерное -: Равноускоренное +: Колебательное -: Апериодическое
7.28. Дифференциальное уравнение движения материальной точки имеет вид 2ּ d 2 x/dt 2+8ּ dx/dt +7ּ x = 0. Определить, каким будет движение: равномерным, равноускоренным, колебательным или апериодическим. Отметьте правильный ответ. -: Равномерное -: Равноускоренное -: Колебательное +: Апериодическое 7.29. Груз массой m = 0,2 кг подвешен к пружине, коэффициентом жёсткости которой с = 20 Н/м, и выведен из состояния равновесия. Сила сопротивления движению R = - 4 ּv (Н). Определить, каким будет движение: равномерным, колебательным или апериодическим. Отметьте правильный ответ. -: Равномерное -: Равнозамедленное -: Колебательное +: Апериодическое
7.30. Дифференциальное уравнение движения материальной точки имеет вид 7ּ d 2 x/dt 2 + 28ּ dx/dt + c ּ x = 0. Определить наибольшее значение коэффициента жёсткости с пружины, при котором движение будет апериодическим; c = … Ответ: 28. 7.3I. Дифференциальное уравнение движения материальной точки имеет вид d 2 x/dt 2 + b ּ dx/dt + 100ּ x = 0. Определить минимальное значение b min точки, при котором движение будет апериодическим; b min = … Ответ: 20
(g – ускорение свободного падения). Ответ: Т = 2 ּπּ 0,91 ּ 7.33.
Ответ: 360
Ответ: 0,44 7.35. Груз, подвешенный к пружине, при медленном его опускании вызвал удлинение её на Δ l = 6 см. Определить период Т (сек.) собственных колебаний пружинного маятника. (g = 9,8 м/с2) Ответ: 0,49 7.36. Человек массы m = 60 кг переходит с носа на корму лодки. На какое расстояние по величине | s |переместится лодка длины l = 4 м, если её масса M = 140 кг? | s | = … (м). Ответ: 1,2
Ответ: 0,5
| Q | = … (кгּм/с). Ответ: 18
Определить модуль количества движения | Q | механизма; | Q | = … (кгּм/с). Ответ: 10
Определить модуль количества движения | Q | механизма; | Q | = … (кгּм/с). Ответ: 16
Определить модуль количества движения | Q | механизма в тот момент, когда угол φ = π /2; | Q | = … (кгּм/с). Ответ: 2
Определить модуль количества движения | Q | механизма в тот момент, когда угол α = 0; | Q | = … (кгּм/с). Ответ: 6
Определить модуль главного вектора внешних сил | F (e) | = … (Н), действующих на тело 2.
Ответ: 20 7.47. Поезд массы m = 600 тонн после прекращения тяги тепловоза останавливается под действием силы трения F тр = 0,2 МН (мега-ньютон) через время t = 45 сек. С какой скоростью v шёл поезд до момента прекращения тяги тепловоза? v = …(м/с) Ответ: 15
7.48. Масса платформы с орудием и боеприпасами составляет M = 20 тонн. С этой платформы, движущейся со скоростью u = 2,5 м/с, производится выстрел из орудия. Снаряд массы m = 25 кг вылетает из ствола орудия со скоростью v = 800 м/с (относительно орудия). Найти скорость платформы u 1 (м/с) непосредственно после выстрела, если направления движения платформы и выстрела совпадают. Ответ: 1,5 7.49. Масса платформы с орудием и боеприпасами составляет M = 20 тонн. С этой платформы, движущейся со скоростью u = 2,5 м/с, производится выстрел из орудия. Снаряд массы m = 25 кг вылетает из ствола орудия со скоростью v = 800 м/с (относительно орудия). Найти скорость платформы u 1 (м/с) непосредственно после выстрела, если направления движения платформы и выстрела противоположны. Ответ: 3,5 7.50. Ядро, летевшее со скоростью v = 200 м/с, разорвалось на два осколка с массами m 1 = 10 кг и m 2 = 5 кг. Скорость первого осколка v 1 = 250 м/с и направлена так же, как и скорость ядра до разрыва. Найти скорость v 2 второго (меньшего) осколка; v 2 = … (м/с). Ответ: 100 7.51. Кривошипно-ползунный механизм Ответ: 0,20 ּωּl 7.52. Орудие, имеющее массу ствола М = 400 кг, стреляет в горизонтальном направлении. Масса снаряда m = 4 кг, его начальная скорость v = 500 м/с. При выстреле ствол откатывается на расстояние s = 40 см. Найти среднюю силу торможения F (кН), возникающую в механизме, тормозящем ствол. Ответ: 12,5 7.53. Тело массы M = 990 г лежит на горизонтальной поверхности. В него попадает пуля массы m = 10 г и застревает в нём. Скорость пули v = 600 м/с и направлена горизонтально. Какой путь s (м) пройдет тело до остановки? Коэффициент трения между телом и поверхностью k = 0,1. (g = 10 м/с2) Ответ: 18
Определить угловую скорость ω стержня в момент прохождения им нижнего положения. Ответ: 1,55 ּ
Момент инерции стержня ОА относительно шарнира О (или стержня СВ относительно шарнира С) равен J = (1/3)ּ m ּ(ОА)2 = (1/3)ּ m ּ(CB)2. Определить кинетическую энергию T механизма. T = … (Дж) Ответ: 60
Определить кинетическую энергию T механизма; T = … (Дж) Ответ: 225 7.57. К концу троса, намотанного на барабан, m 1 = m, m 2 = (2/9)ּ m. Определить ускорение тела 1. Ответ: 0,90 ּ 7.58. Дано: m 1, колесо массы m 2 – Ответ: 0,25 ּg
Ответ: 0,30 ּg 7.60. Дано: масса груза m 1, угол α, каток массы Ответ: 0,50 ּgּsinα
“Нулевой” вариант заданий экзаменационных тестов ЦКТ Механике; 2013/2014 учебный год С т а т и к а
Тема 8. Основные понятия, аксиомы и основная теорема статики.
|
||||
|
Последнее изменение этой страницы: 2016-04-07; просмотров: 1033; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 13.59.82.60 (0.012 с.) |

 7.2. Материальная точка массой m = 0,5 кг брошена с поверхности Земли с начальной скоростью v 0= 25 м/с и в положении М имеет скорость v = 15 м/с. Определить работу силы тяжести (Дж) при перемещении точки из положения М 0 в положение М.
7.2. Материальная точка массой m = 0,5 кг брошена с поверхности Земли с начальной скоростью v 0= 25 м/с и в положении М имеет скорость v = 15 м/с. Определить работу силы тяжести (Дж) при перемещении точки из положения М 0 в положение М. 7.3. Груз М весом Р = 20 Н, прикреплённый к невесомой нити длиной l = ОМ = 90 см, начинает двигаться из состояния покоя. Определить: 1) работу силы тяжести А (Р) на перемещении М1М2; 2) скорость v груза М, когда он займёт положение М2. Принять g = 10 м/с2.
7.3. Груз М весом Р = 20 Н, прикреплённый к невесомой нити длиной l = ОМ = 90 см, начинает двигаться из состояния покоя. Определить: 1) работу силы тяжести А (Р) на перемещении М1М2; 2) скорость v груза М, когда он займёт положение М2. Принять g = 10 м/с2. = … (Дж), 2)
= … (Дж), 2)  = … (м/с).
= … (м/с). Груз М весом Р подвешен на невесомой нерастяжимой нити длиной l. В начальный момент времени груз находился в положении М1.
Груз М весом Р подвешен на невесомой нерастяжимой нити длиной l. В начальный момент времени груз находился в положении М1. Ответы: – 0,5*1
Ответы: – 0,5*1 7.6. Матер. точка массы m = 2 кг перемещается в вертикальной плоскости Оху. Определить работу А ОМ (Дж) силы тяжести Р = mּg при перемещении матер. точки по дуге OM окружности радиуса R = 10 м (см. рис.). Ускорение свободного падения принять равным g = 9,8 м/с2. Результат вычисления округлить до ближайшего целого числа. А ОМ = … (Дж)
7.6. Матер. точка массы m = 2 кг перемещается в вертикальной плоскости Оху. Определить работу А ОМ (Дж) силы тяжести Р = mּg при перемещении матер. точки по дуге OM окружности радиуса R = 10 м (см. рис.). Ускорение свободного падения принять равным g = 9,8 м/с2. Результат вычисления округлить до ближайшего целого числа. А ОМ = … (Дж) Матер. точка массы m движется в горизонтальной плоскости Oxy под действием силы, пропорциональной смещению точки от точки от центра О и направленной к этому центру
Матер. точка массы m движется в горизонтальной плоскости Oxy под действием силы, пропорциональной смещению точки от точки от центра О и направленной к этому центру  , где
, где  - радиус-вектор точки, c = 20 Н/см. Вычислить работу А 12 силы
- радиус-вектор точки, c = 20 Н/см. Вычислить работу А 12 силы  при перемещении матер. точки из точки М 1 в точку М 2 (см. рис.); а = 8 см.
при перемещении матер. точки из точки М 1 в точку М 2 (см. рис.); а = 8 см. 7.8. Матер. точка массы m движется в горизонтальной плоскости Oxy под действием силы, пропорциональной смещению точки от точки от центра О и направленной к этому центру
7.8. Матер. точка массы m движется в горизонтальной плоскости Oxy под действием силы, пропорциональной смещению точки от точки от центра О и направленной к этому центру  , где
, где  - радиус-вектор точки, c = 20 Н/см. Вычислить работу А 12 силы
- радиус-вектор точки, c = 20 Н/см. Вычислить работу А 12 силы  7.9. Матер. точка массы m движется в горизонтальной плоскости Oxy под действием силы притяжения
7.9. Матер. точка массы m движется в горизонтальной плоскости Oxy под действием силы притяжения  / r 3 к силовому центру О, убывающей по величине обратно пропорционально квадрату расстояния от точки до силового центра О, | F |= k / r 2, k = 200 (Н/м2). Вычислить работу А 12 силы
/ r 3 к силовому центру О, убывающей по величине обратно пропорционально квадрату расстояния от точки до силового центра О, | F |= k / r 2, k = 200 (Н/м2). Вычислить работу А 12 силы  , где k = const. (Центр окружности совпадает с силовым центром.) Определить значение скорости v точки при следующих числовых данных параметров: k = 16 м3/сек2 и r = 4 м. v = … (м/с).
, где k = const. (Центр окружности совпадает с силовым центром.) Определить значение скорости v точки при следующих числовых данных параметров: k = 16 м3/сек2 и r = 4 м. v = … (м/с). , постоянной по модулю (|
, постоянной по модулю (|  | = F = const), действующей в области 0,01 м < r < 2 м. (Центр окружности совпадает с силовым центром.) Определить значение скорости v (м/с) точки при следующих числовых данных параметров: F = 1 (Н), m = 0,25 (кг), r = 1 (м). v = … (м/с).
| = F = const), действующей в области 0,01 м < r < 2 м. (Центр окружности совпадает с силовым центром.) Определить значение скорости v (м/с) точки при следующих числовых данных параметров: F = 1 (Н), m = 0,25 (кг), r = 1 (м). v = … (м/с). 7.13. Матер. точка массы m движется в горизонтальной плоскости Oxy под действием силы, пропорциональной смещению точки от точки от центра О и направленной к этому центру
7.13. Матер. точка массы m движется в горизонтальной плоскости Oxy под действием силы, пропорциональной смещению точки от точки от центра О и направленной к этому центру  7.14. Матер. точка массы m движется в горизонтальной плоскости Oxy под действием силы, пропорциональной смещению точки от точки от центра О и направленной к этому центру
7.14. Матер. точка массы m движется в горизонтальной плоскости Oxy под действием силы, пропорциональной смещению точки от точки от центра О и направленной к этому центру  Матер. точка массы m движется в горизонтальной плоскости Oxy под действием силы, пропорциональной смещению точки от точки от центра О и направленной к этому центру
Матер. точка массы m движется в горизонтальной плоскости Oxy под действием силы, пропорциональной смещению точки от точки от центра О и направленной к этому центру  Ответ: 25,2
Ответ: 25,2 7.17. На рис. изображена штанга, которая может вращаться вокруг горизонтальной оси шарнира О. Плечи штанги l 1 = 30 см и l 2 = 70 см. На концах штанги закреплены точечные грузы с массами m 1 = 8 кг и m 2 = 4 кг. Штанга совершает поворот вокруг оси О в вертикальной плоскости на угол 90о по часовой стрелке.
7.17. На рис. изображена штанга, которая может вращаться вокруг горизонтальной оси шарнира О. Плечи штанги l 1 = 30 см и l 2 = 70 см. На концах штанги закреплены точечные грузы с массами m 1 = 8 кг и m 2 = 4 кг. Штанга совершает поворот вокруг оси О в вертикальной плоскости на угол 90о по часовой стрелке. 7.19. Груз массой m прикреплён к правому концу пружины, левый конец которой закреплён в стене. В начальном положении пружина не была деформирована. Ось x направлена вдоль оси пружины, причём начало отсчёта находится в правом конце не деформированной пружины.
7.19. Груз массой m прикреплён к правому концу пружины, левый конец которой закреплён в стене. В начальном положении пружина не была деформирована. Ось x направлена вдоль оси пружины, причём начало отсчёта находится в правом конце не деформированной пружины. 7.32. Маятник представляет собой шарнирно соединённую со штативом лёгкую жёсткую спицу с закреплёнными на ней двумя небольшими по размерам грузами массы m каждый (см. рис.). Расстояния между точкой крепления О и верхним грузом и между грузами равны 0,5ּ l. Определить период колебаний.
7.32. Маятник представляет собой шарнирно соединённую со штативом лёгкую жёсткую спицу с закреплёнными на ней двумя небольшими по размерам грузами массы m каждый (см. рис.). Расстояния между точкой крепления О и верхним грузом и между грузами равны 0,5ּ l. Определить период колебаний.
 Тело массы m = 0,4 кг совершает колебания на пружине так, что наибольшее значение скорости v макс = 120 см/сек, наибольшее отклонение от положения равновесия x макс = 4 см Определить коэффициент жёсткости c (Н/м) пружины.
Тело массы m = 0,4 кг совершает колебания на пружине так, что наибольшее значение скорости v макс = 120 см/сек, наибольшее отклонение от положения равновесия x макс = 4 см Определить коэффициент жёсткости c (Н/м) пружины. 7.34. Через неподвижный блок с массой m 1 = 200 г перекинута нить, к концу которой подвешен груз массы m 2 = 390 г. Другой конец нити привязан к пружинке с закреплённым нижним концом (см. рис.). Коэффициент жёсткости пружины c = 100 (Н/м). Вычислить период колебаний груза Т (сек.). Нить не может скользить по поверхности блока; блок однородный цилиндр; трение в оси блока отсутствует.
7.34. Через неподвижный блок с массой m 1 = 200 г перекинута нить, к концу которой подвешен груз массы m 2 = 390 г. Другой конец нити привязан к пружинке с закреплённым нижним концом (см. рис.). Коэффициент жёсткости пружины c = 100 (Н/м). Вычислить период колебаний груза Т (сек.). Нить не может скользить по поверхности блока; блок однородный цилиндр; трение в оси блока отсутствует.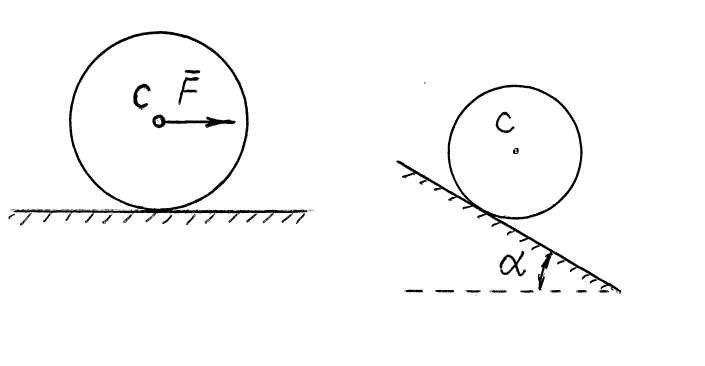 7.37. Колесо радиуса R = 0,5 м, массы m = 10 кг и моментом инерции относительно оси вращения J = 1,5 кгּм2 катится без скольжения по горизонтальной прямой под действием приложенной к нему силы F в центре масс С колеса горизонтально, F = 8 Н. Определить ускорение a C (м/с2) центра масс C колеса. a C = …
7.37. Колесо радиуса R = 0,5 м, массы m = 10 кг и моментом инерции относительно оси вращения J = 1,5 кгּм2 катится без скольжения по горизонтальной прямой под действием приложенной к нему силы F в центре масс С колеса горизонтально, F = 8 Н. Определить ускорение a C (м/с2) центра масс C колеса. a C = … 7.38. Шкив 1 массы М = 10 кг и радиуса R = 0,3 м, вращаясь с угловой скоростью ω = 4,0 рад/с, поднимает груз 2 массы m = 15 кг. Определить модуль количества движения | Q | механизма;
7.38. Шкив 1 массы М = 10 кг и радиуса R = 0,3 м, вращаясь с угловой скоростью ω = 4,0 рад/с, поднимает груз 2 массы m = 15 кг. Определить модуль количества движения | Q | механизма; 7.39. Масса каждого из тёх звеньев шарнирного параллелограмма ОАВС (ОА, АВ, СВ)равна 2 кг. Длина кривошипа ОА равна 0,5 м. Кривошип ОА вращается равномерно с угловой скоростью ω = 5 рад/с.
7.39. Масса каждого из тёх звеньев шарнирного параллелограмма ОАВС (ОА, АВ, СВ)равна 2 кг. Длина кривошипа ОА равна 0,5 м. Кривошип ОА вращается равномерно с угловой скоростью ω = 5 рад/с. 7.44. Цилиндр 1 вращается с угловой скоростью ω = 20 рад/с. Его момент инерции относительно оси вращения Ј = 10 кгּм2, радиус r = 0,4 м. Груз 2 имеет массу m 2 = 2 кг.
7.44. Цилиндр 1 вращается с угловой скоростью ω = 20 рад/с. Его момент инерции относительно оси вращения Ј = 10 кгּм2, радиус r = 0,4 м. Груз 2 имеет массу m 2 = 2 кг. 7.45. В кривошипно-шатунном механизме ОАВ, расположенном в горизонтальной плоскости, кривошип ОА и шатун АВ имеют каждый массу m = 2 кг, а ползун В имеет массу m /2 = 1 кг. Длина кривошипа OA l = 0,5 м, длина шатуна AB 2ּ l = 1,0 м. Угловая скорость кривошипа равна ω = 6 рад/с.
7.45. В кривошипно-шатунном механизме ОАВ, расположенном в горизонтальной плоскости, кривошип ОА и шатун АВ имеют каждый массу m = 2 кг, а ползун В имеет массу m /2 = 1 кг. Длина кривошипа OA l = 0,5 м, длина шатуна AB 2ּ l = 1,0 м. Угловая скорость кривошипа равна ω = 6 рад/с. 7.46. В кривошипно-шатунном механизме ОАВ, расположенном в горизонтальной плоскости, кривошип ОА и шатун АВ имеют каждый массу m = 2 кг и длину l = 0,5 м, а ползун В имеет массу m /2 = 1 кг. Угловая скорость кривошипа равна ω = 6 рад/с.
7.46. В кривошипно-шатунном механизме ОАВ, расположенном в горизонтальной плоскости, кривошип ОА и шатун АВ имеют каждый массу m = 2 кг и длину l = 0,5 м, а ползун В имеет массу m /2 = 1 кг. Угловая скорость кривошипа равна ω = 6 рад/с. прикреплён к станине массы M, установленной на гладком горизонтальном фундаменте. Масса ползуна B механизма равна m, масса станины M = 4ּ m. Длины звеньев OA и AB: OA = l, AB = 2ּ l, их массами пренебречь. Кривошип вращается с постоянной угловой скоростью ω и при t = 0 угол φ = 0 и в этот момент скорость станины равна нулю. Определить максимальное значение v max скорости станины.
прикреплён к станине массы M, установленной на гладком горизонтальном фундаменте. Масса ползуна B механизма равна m, масса станины M = 4ּ m. Длины звеньев OA и AB: OA = l, AB = 2ּ l, их массами пренебречь. Кривошип вращается с постоянной угловой скоростью ω и при t = 0 угол φ = 0 и в этот момент скорость станины равна нулю. Определить максимальное значение v max скорости станины. 7.54. Стержень представляет собой шарнирно соединённую со штативом лёгкую жёсткую спицу с закреплёнными на ней двумя небольшими по размерам грузами массы m каждый (см. рис.); расстояния между точкой крепления О и верхним грузом и между грузами равны l. Первоначально стержень был отклонён в верхнее вертикальное положение, а затем лёгким толчком был выведен из этого положения.(g – ускорение свободного падения).
7.54. Стержень представляет собой шарнирно соединённую со штативом лёгкую жёсткую спицу с закреплёнными на ней двумя небольшими по размерам грузами массы m каждый (см. рис.); расстояния между точкой крепления О и верхним грузом и между грузами равны l. Первоначально стержень был отклонён в верхнее вертикальное положение, а затем лёгким толчком был выведен из этого положения.(g – ускорение свободного падения).
 прикреплён груз 1 массы m 1. К барабану ворота 2 радиуса r и массы m 2 приложен постоянный вращающий момент M. Барабан однородный диск.
прикреплён груз 1 массы m 1. К барабану ворота 2 радиуса r и массы m 2 приложен постоянный вращающий момент M. Барабан однородный диск.
 однородный цилиндр, причем m 2 = 8 ּm 1. Пренебрегая массой блока и каната, также проскальзыванием колеса и силой трения, определить ускорение груза 1.
однородный цилиндр, причем m 2 = 8 ּm 1. Пренебрегая массой блока и каната, также проскальзыванием колеса и силой трения, определить ускорение груза 1. 7.59. Дано: груз массы m 1, колесо массы m 2 – однородный цилиндр, причем m 2 =
7.59. Дано: груз массы m 1, колесо массы m 2 – однородный цилиндр, причем m 2 =  ּm 1. Пренебрегая массой блока и каната, также проскальзыванием колеса и силой трения в блоке, определить ускорение груза 1.
ּm 1. Пренебрегая массой блока и каната, также проскальзыванием колеса и силой трения в блоке, определить ускорение груза 1. m 2 – однородный цилиндр, причем m 2 = 1,6 ּm 1. Пренебрегая массой блока и каната, также проскальзыванием катка и силой трения в блоке, определить ускорение груза 1.
m 2 – однородный цилиндр, причем m 2 = 1,6 ּm 1. Пренебрегая массой блока и каната, также проскальзыванием катка и силой трения в блоке, определить ускорение груза 1.


