
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Основные кинематические характеристики движения мат точки.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте Основные кинематические характеристики движения мат точки. Способы описания движения мат точки. Описание перемещения, скорости и ускорения в векторной и координатной форме. Криволинейное движение мат точки. Движение мат точки по окружности. Векторы угловой скорости и углового ускорения. Кинематика твёрдого тела. Поступательное движение твёрдого тела. Вращательное движение твёрдого тела вокруг неподвижной оси. Плоскопараллельное движение твёрдого тела. 10. Инерциальные системы отсчёта. Преобразования Галилея. Инварианты преобразований. Классический закон сложения скоростей. Механический принцип относительности. Взаимодействия и силы. Силы в механике. Первый закон Ньютона. Масса тела. Второй и третий законы Ньютона. Интерпретация третьего закона Ньютона при взаимодействии движущихся электрических зарядов. Неинерциальные системы отсчёта. Силы инерции. Центробежная сила инерции. Кориолисова сила инерции. Закон всемирного тяготения. Энергия гравитационного взаимодействия. Система мат точек и её импульс. Уравнение движения системы мат точек. Центр масс системы мат точек. Теорема о движении центра масс системы мат точек. Система центра масс. Закон сохранения импульса для изолированной системы. Реактивное движение. Уравнение Мещерского. Формула Циалковского. 19. Движение искусственных спутников Земли, 1, 2 и 3-ья космические скорости, Стационарное движение жидкости. Линии и трубки тока. Уравнение неразрывности струи. Уравнение Бернулли. Полная энергии потока. Лиминарное и турбулентное течения. Число Рейнольдса. Обтекание тел жидкостью и газом. Подъёмная сила и лобовое сопротивление. Эффект Магнуса. Ламинарное течение в трубах. Формула Пуазейля. Столкновения. Упругие и неупругие. Коэффициент восстановления относительной скорости. Предмет, задачи и методы молекулярной физики. Статистический, термодинамический и динамический методы описания мат тел. Модели мат точки, твёрдого тела и мат тела. 35. Модель идеального газа. Массы атомов и молекул. Количество вещества. Число Авогадро и его опытное определение. Координатный способ. В этом случае положение материально точки на плоскости в произвольный момент времени определяется координатами X и Y, которые представляют собой проекции радиус вектора тела на оси. При движении тела координаты его изменяются во времени, являясь функциями (T): X(T) = X, Y(T) = Y, если эти функции известны, то они определяют положение тела в любой момент времени. Зная эти зависимости, можно найти положение тела, проекции на его скорость, модуль и направление a и V в любой момент времени.
Естественный способ. Применяется, если траектория материальной точки известна заранее. На заданной траектории выбирают начало отсчёта - неподвижную точку, а положение материальной точки определяют при помощи дуговой координаты, представляющей собой расстояние вдоль траектории от выбранного начала отсчета до самой материальной точки.
Движение тела считается определённым, если известны его траектория, начало отсчета, положительное направление дуговой координаты и зависимость времени от этой координаты. Перемещение тела – вектор, соединяющий начальное и конечное положение тела. Средняя скорость – отношение перемещения тела к времени. Средняя путевая скорость – отношение пути к времени, за которое был пройден этот путь. Мгновенная скорость – величина, к которой стремится отношение при стремление ∆t к нулю. Вектор мгновенной скорости направлен по касательной к траектории в данной точке в сторону движения тела. В системе СИ длина измеряется в метрах (м), ускорение – метр на секунду в квадрате, скорость – метр на секунду (м\с), время – в секундах (с). Рис. 1.19. Траектория и вектор перемещения при криволинейном движении. При движении по криволинейной траектории вектор перемещения
Рис. 1.20. Мгновенная скорость при криволинейном движении. Криволинейное движение – это всегда ускоренное движение. То есть ускорение при криволинейном движении присутствует всегда, даже если модуль скорости не изменяется, а изменяется только направление скорости. Изменение величины скорости за единицу времени – это тангенциальное ускорение:
или
Где vτ, v0 – величины скоростей в момент времени t0 + Δt и t0 соответственно. Тангенциальное ускорение в данной точке траектории по направлению совпадает с направлением скорости движения тела или противоположно ему. Нормальное ускорение - это изменение скорости по направлению за единицу времени:
Нормальное ускорение направлено по радиусу кривизны траектории (к оси вращения). Нормальное ускорение перпендикулярно направлению скорости. Центростремительное ускорение – это нормальное ускорение при равномерном движении по окружности. Полное ускорение при равнопеременном криволинейном движении тела равно:
Движение тела по криволинейной траектории можно приближённо представить как движение по дугам некоторых окружностей (рис. 1.21).
Движение точки по окружности может быть очень сложным (рис. 17). Рассмотрим подробно движение точки по окружности, при котором v = const. Такое движение называется равномерным движением по окружности. Естественно, вектор скорости не может быть неизменным (v не равно const), так как направление скорости постоянно меняется. Время, за которое траектория точки опишет окружность, называется периодом обращения точки (Т). Число оборотов точки в одну секунду называется частотой обращения (v). Период обращения можно найти по формуле:
Естественно, перемещение точки за один оборот будет равно нулю. Однако пройденный путь будет равен 2ПиR, а при числе оборотов п путь будет равен 2ПиRn или 2ПиRt/T, где t - время движения. Ускорение при равномерном движении точки по окружности направлено к ее центру и численно равно а = v2/R. Это ускорение называется центростремительным (или нормальным). Вывод этого равенства может быть следующим. Приведем векторы скорости к одной точке хотя бы за - Т (можно и за Т/2 или Т) (рис. 18).
Тогда сумма изменений векторов скоростей за малые промежутки времени будет равна длине дуги АВ, которая равна модулю | v2 - v1 | за время t = 1/4*Т. Определим длину дуги. Поскольку радиусом для дуги будет модуль вектора v1=v2=v, то длина дуги l может быть вычислена как длина четверти окружности с радиусом v:
После сокращения получим:
Если же движение равнопеременное, то v Ф const, тогда рассматривают другую составляющую ускорения, обеспечивающую изменение модуля скорости. Это ускорение называется тангенциальным:
Тангенциальное ускорение направлено по касательной к траектории, оно может совпадать по направлению со скоростью (движение равноускоренное) или быть противоположно направленным (движение равнозамедленное). Кинематика твердого тела В кинематике твердого тела определяются: закон движения и кинематические характеристики тела, а также кинематические характеристики точек тела.
В данном методическом пособии рассмотрены следующие виды движения твердого тела: - поступательное; - вращательное; - плоскопараллельное. Поступательное движение Поступательное движение – это движение, при котором любая прямая, связанная с телом, перемещается параллельно самой себе.
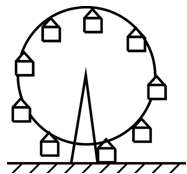
На рисунках 2.1,а и 2.1,б приведены примеры поступательного движения: движение прямоугольника в плоскости чертежа, движение каждой кабины колеса обозрения.
а б Рисунок 2.1
Рисунок 2.2 Исходя из определения поступательного движения, движение твердого тела может быть задано в векторном виде формулой (рисунок 2.2): rM=rA ⊕ AM.
В этой формуле AM - вектор постоянный по величине и направлению, поэтому производная от него равна нулю. Для скорости и ускорения произвольной точки M получим:
То есть скорости и ускорения точек твердого тела при поступательном движении равны и одинаково направлены, а траектории при наложении совпадают.
Для определения кинематических характеристик точек тела достаточно знать закон движения одной из них.
Движение твердого тела, при котором две его точки О и О ' остаются неподвижными, называется вращательным движением вокруг неподвижной оси, а неподвижную прямую ОО ' называют осью вращения.
Рис. 2.12 Проследим за некоторой точкой М этого твердого тела. За время dt точка М совершает элементарное перемещение d r.
Угловой скоростью называется вектор
Если ω – const, то имеет место равномерное вращение тела вокруг неподвижной оси. Пусть v – линейная скорость точки М. За промежуток времени dt точка М проходит путь dr = vdt. В то же время dr = Rd φ (dφ - центральный угол). Тогда, можно получить связь линейной скорости и угловой:
В векторной форме Наряду с угловой скоростью вращения используют понятия периода и частоты вращения.
Введем вектор углового ускорения
Вектор
Рис. 2.13 Как и любая точка твердого тела, точка М имеет нормальную и тангенциальную составляющие ускорения. Выразим нормальное и тангенциальное ускорение точки М через угловую скорость и угловое ускорение:
Обратите внимание. Все кинематические параметры, характеризующие вращательное движение (угловое ускорение, угловая скорость и угол поворота), направлены вдоль оси вращения. равномерное вращение ε = 0; ω = const; φ = φ0 ± ω t, равнопеременное вращение
Плоскопараллельным (плоским) движением (ППД) твердого тела называется такое движение, при котором все точки тела перемещаются в плоскостях параллельных некоторой неподвижной плоскости (рисунок 2.11).
При таком движении точки, лежащие в разных плоскостях на одном отрезке, перпендикулярном неподвижной плоскости (например M1M2) совершают одинаковые движения.
Рисунок 2.11
Рисунок 2.12
Отрезок M1M2 движется поступательно. Поэтому изучение плоскопараллельного движения сводится к изучению движения плоской фигуры в какой-то плоскости.
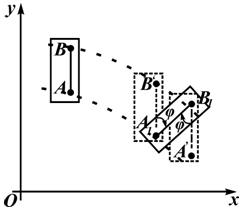
На рисунке 2.12 показано перемещение пластинки в плоской системе отсчета xOy из одного положения в другое. Такое перемещение можно осуществить двигая пластину поступательно с траекторией точки A с последующим поворотом на угол φ вокруг точки A1. Это же перемещение можно выполнить иначе.
Например, перемещая пластинку поступательно с траекторией точки B, с последующим поворотом вокруг B1 на угол φ. Траектории точек A и B различны, а угол поворота в обоих случаях одинаков.
Положение пластинки вполне определяется положением скрепленного с ней отрезка (например AB), закон движения которого можно задать в виде: xA=xA(t), yA=yA(t), φ=φ(t). Точка A в этом случае называется полюсом. Если принять за полюс точку B, то получим уравнения: x B=xB(t), yB=yB(t), φ=φ(t)
За полюс выбирается точка, закон движения которой известен.
ИНЕРЦИАЛЬНАЯ система ОТСЧЕТА - система отсчета, в которой справедлив закон инерции: материальная точка, на которую не действуют никакие силы, находится в состоянии покоя или равномерного прямолинейного движения. Любая система отсчета, движущаяся относительно инерциальной системы отсчета поступательно, равномерно и прямолинейно, также является инерциальной системой отсчета. Все инерциальные системы отсчета равноправны, т. е. во всех таких системах законы физики одинаковы. Преобразования Галилея. Рассмотрим две системы отсчета движущиеся друг относительно друга и с постоянной скоростью v0.Одну из этих систем обозначим буквой K. Будем считать неподвижной. Тогда вторая система K будет двигаться прямолинейно и равномерно. Выберем координатные оси x,y,z системы K и x',y',z' системы K' так что оси x и x' совпадали, а оси y и y', z и z', были параллельны друг другу. Найдем связь между координатами x,y,z некоторой точки P в системе K и координатами x',y',z' той же точки в системе K'. Если начать отсчёт времени с того момента, когда начало координат системы, совпадали, то x=x'+v0, кроме того, очевидно, что y=y', z=z'. Добавим к этим соотношениям принятое в классической механике предположение, что время в обеих системах течёт одинаковым образом, то есть t=t'. Получим совокупность четырёх уравнений: x=x'+v0t;y=y';z=z';t=t', названных преобразованиями Галилея Инвариантами преобразования Галилея являются длина тел и промежуток времени между событиями. Именно поэтому понятия длины и промежутка времени играют такую большую роль в классической физике. [ 4 ] Дифференциал dr являетсяинвариантом преобразований Лоренца, т.е. интервалом времени, не зависящим от ситуации - подвижной или неподвижной является исходная система отсчета. Ньютона о существовании некоего универсального, абсолютного времени. [ 13 ] скорость тела относительно неподвижной системы отсчета равна векторной сумме скорости тела относительно движущейся системы и скорости самой движущейся системы относительно неподвижной
В классической механике справедлив механический принцип относительности: законы динамики одинаковы во всех инерциальных системах отсчета. Рассмотрим две системы отсчета: инерциальную систему К (с координатами x, y, z), условно будем считать неподвижной, и систему К' (с координатами x', y', z'), движущуюся относительно К равномерно и прямолинейно со скоростью υ0 (υ0=const)
Координата точки А по отношению к системе К: х = х' + 00', за промежуток времени t от начала отсчета будет:
Уравнения (3.19) носят название преобразования координат и времени Галилея. Отсчет времени начат с момента, когда начало координат обеих систем совпадают. Продифференцировав по времени t, получим выражение правила сложения скоростей в классической механике: υ=υ'+υ0 (3.20) Ускорения в обеих системах отсчета одинаковы, а это означает, что поведение тел в обеих системах одинаково: a=a' (3.21), т.е. из соотношения (3.21) вытекает подтверждение механического принципа относительности: уравнения динамики при переходе от одной инерциальной системы отсчета к другой не изменяются, т.е. являются инвариантными по отношению к преобразованиям Галилея. Механический принцип относительности можно сформулировать еще следующим образом: никакими механическими опытами, проведенными в данной инерциальной системе отсчета, нельзя установить, покоится ли она или движется равномерно и прямолинейно. Например, сидя в каюте корабля, движущегося равномерно и прямолинейно, мы не можем определить, покоится корабль или движется, не выглянув в окно.
11. Закон ньютона Существуют такие системы отсчёта, называемые инерциальными, относительно которых материальные точки, когда на них не действуют никакие силы (или действуют силы взаимно уравновешенные), находятся в состоянии покоя или равномерного прямолинейного движения. Всякое тело продолжает удерживаться в состоянии покоя или равномерного и прямолинейного движения, пока и поскольку оно не понуждается приложенными силами изменить это состояние. С современной точки зрения, такая формулировка неудовлетворительна. Во-первых, термин «тело» следует заменить термином «материальная точка», так как тело конечных размеров в отсутствие внешних сил может совершать и вращательное движение. Во-вторых, и это главное, Ньютон в своём труде опирался на существование абсолютной неподвижной системы отсчёта, то есть абсолютного пространства и времени, а это представление современная физика отвергает. С другой стороны, в произвольной (скажем, вращающейся) системе отсчёта закон инерции неверен, поэтому ньютоновская формулировка была заменена постулатом существования инерциальных систем отсчета. 12. Второй закон В инерциальной системе отсчёта ускорение, которое получает материальная точка с постоянной массой, прямо пропорционально равнодействующей всех приложенных к ней сил и обратно пропорционально её массе.
В инерциальной системе отсчета скорость изменения импульса материальной точки равна равнодействующей всех приложенных к ней внешних сил.
Третий закон ньютона Материальные точки взаимодействуют друг с другом силами, имеющими одинаковую природу, направленными вдоль прямой, соединяющей эти точки, равными по модулю и противоположными по направлению:
Закон утверждает, что силы возникают лишь попарно, причём любая сила, действующая на тело, имеет источник происхождения в виде другого тела. Иначе говоря, сила всегда есть результат взаимодействия тел. Существование сил, возникших самостоятельно, без взаимодействующих тел, невозможно. 13. 14. Закон всемирного тяготения. Энергия гравитационного взаимодействия. закон всемирного тяготения: все тела притягиваются друг к другу, сила всемирного тяготения прямо пропорциональна произведению масс тел и обратно пропорциональна квадрату расстояния между ними:
Векторы сил всемирного тяготения направлены вдоль прямой, соединяющей тела. Гравитационная энергия — потенциальная энергия системы тел (частиц), обусловленная их взаимным гравитационным тяготением
15. 16. 17. 18. 19. 20. Работа постоянной и переменной силы. Потенциальные силы. Мощность. 1. Если на тело действует постоянная сила F (Рисунок 13), и это приводит к перемещению ∆ r тела, то элементарной работой ∆А постоянной силы называется скалярное произведение вектора силы F и вектора перемещения ∆r: ∆А = (F∙∆r) = ½ F½½∆ r½ cos a, где a - угол между направлениями векторов силы F и перемещения ∆r, (F∙ ∆r) – скалярное произведение двух векторов (см.[8]).
Работа ∆А - скаляр. Если угол a - острый, то ∆А положительная величина, и говорят, что сила совершает работу. Если угол a - тупой, то ∆А - отрицательная величина, и говорят, что работа совершается против действия силы. Если a = 900, т.е. направления силы и перемещения взаимно перпендикулярны, то такая сила работы не совершает ∆А = 0. Такая сила не может изменить величину скорости тела, но она меняет направление скорости. 2. Работа переменной силы. Если сила или равнодействующая сил изменяет свою величину или направление (движение по криволинейной траектории, причем угол α ≠ 900), то работа ∆А, совершаемая переменной силой F (или Fрез) на конечном участке траектории вычисляется следующим образом. На рисунке 14 представлен график зависимости силы F от пути S. Разобьем весь путь на N участков. Перемещение и действующая сила на каждом участке соответственно равны F i и ∆ r i. Тогда работа А, совершаемая силой F, равна алгебраической сумме работ, совершаемых каждой из сил F i на своем малом участке (Рисунок 14): А = ∆А1 + ∆А2 +....+ ∆А N = (F1∙∆ r1) + (F 2∙∆ r2) +...+(F N∙∆ rN) = (Fi∙∆ ri), где i = 1,2...... N - номер элементарного участка траектории.
На участке ∆r i силу Fi можно считать постоянной, тогда элементарная работа ∆Аi на участке ∆r i равна ∆Аi= Fi∙∆ r i и равна площади заштрихованной фигуры на рисунке 14. А=∆Аi - это работа силы F на участке r, равна она численно площади S фигуры, ограниченной кривой зависимости F(х) и осью Х. ПОТЕНЦИАЛЬНЫЕ СИЛЫ - силы, работа которых зависит только от начального и конечного положения точек их приложения и не зависит ни от вида траекторий, ни от закона движения этих точек Мо́щность — физическая величина, равная отношению работы ко времени, за которое она была совершена. В более узком смысле мощность равна отношению работы, выполняемой за некоторый промежуток времени, к этому промежутку времени[1]. Различают среднюю мощность за промежуток времени
мгновенную мощность в данный момент времени:
Потенциальная энергия Потенциальная энергия принимается равной нулю для некоторой конфигурации тел в пространстве, выбор которой определяется удобством дальнейших вычислений. Процесс выбора данной конфигурации называется нормировкой потенциальной энергии. Корректное определение потенциальной энергии может быть дано только в поле сил, работа которых зависит только от начального и конечного положения тела, но не от траектории его перемещения. Такие силы называются консервативными. Также потенциальная энергия является характеристикой взаимодействия нескольких тел или тела и поля. Любая физическая система стремится к состоянию с наименьшей потенциальной энергией. Потенциальная энергия упругой деформации характеризует взаимодействие между собой частей тела.
· В то время, как кинетическая энергия всегда характеризует тело относительно выбранной системы отсчёта, потенциальная энергия всегда характеризует тело относительно источника поля. · Кинетическая энергия характеризуется скоростью относительно системы отсчёта; потенциальная — расположением тел в поле. · Основной физический смысл имеет не само значение потенциальной энергии, а её изменение.
Потенциальная энергия зависит от положения тела. В зависимости от того, куда мы будем (чуть-чуть) смещаться от данной точки, потенциальная энергия будет либо уменьшаться, либо увеличиваться. Вот здесь и живет связь между потенциальной энергией и силой. Сила показывает направление, в котором потенциальная энергия уменьшается быстрее всего, а величина силы определяется скоростью изменения. Другими словами, сила - градиент потенциальной энергии.
В изолированной системе тел положительная работа внутренних сил увеличивает кинетическую энергию и уменьшает потенциальную. Отрицательная работа, напротив, увеличивает потенциальную энергию и уменьшает кинетическую. Именно благодаря этому выполняется закон сохранения энергии.
В то же время эта работа равна уменьшению потенциальной энергии:
Работа силы всемирного тяготения, действующей со стороны камня на Землю, практически равна нулю. Из-за большой массы Земли ее перемещением и изменением скорости можно пренебречь. Так как в формулах (6.24) и (6.25) левые части одинаковы, то равны и правые части:
Равенство (6.26) означает, что увеличение кинетической энергии системы равно убыли ее потенциальной энергии (или наоборот). Отсюда вытекает, что
или
Изменение суммы кинетической и потенциальной энергий системы равно нулю.
Так как изменение полной энергии системы в рассматриваемом случае согласно уравнению (6.27) равно нулю, то энергия остается постоянной:
Таким образом, в изолированной системе, в которой действуют консервативные силы, механическая энергия сохраняется. В этом состоит закон сохранения механической энергии. Энергия не создается и не уничтожается, а только превращается из одной формы в другую: из кинетической в потенциальную и наоборот.
или
Это уравнение позволяет очень просто найти скорость камня v2 на любой высоте h2 над землей, если известна начальная скорость v1 камня на исходной высоте h1.
Полная механическая энергия системы равна сумме ее кинетической и потенциальной энергий. В изолированной системе, в которой действуют только консервативные силы, механическая энергия сохраняется.
Пусть Момент Момент Последнее равенство – уравнение моментов. Для системы материальных точек моменты всех внутренних сил равны нулю и мы можем записать уравнение моментов для множества материальных точек так: Закон сохране |
|||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-06; просмотров: 2619; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.214 (0.017 с.) |

 направлен по хорде (рис. 1.19), а l – длина траектории. Мгновенная скорость движения тела (то есть скорость тела в данной точке траектории) направлена по касательной в той точке траектории, где в данный момент находится движущееся тело (рис. 1.20).
направлен по хорде (рис. 1.19), а l – длина траектории. Мгновенная скорость движения тела (то есть скорость тела в данной точке траектории) направлена по касательной в той точке траектории, где в данный момент находится движущееся тело (рис. 1.20).










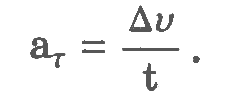


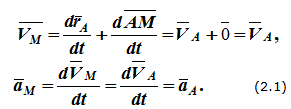

 , ни вторая производная
, ни вторая производная  не могут служить характеристикой движения всего твердого тела.
не могут служить характеристикой движения всего твердого тела.  , проведенный из точки 0 ' в точку М, повернется на угол d φ. На такой же угол повернется радиус-вектор любой другой точки (т.к. тело абсолютно твердое, в противном случае расстояние между точками должно измениться).
, проведенный из точки 0 ' в точку М, повернется на угол d φ. На такой же угол повернется радиус-вектор любой другой точки (т.к. тело абсолютно твердое, в противном случае расстояние между точками должно измениться). 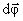 – вектор элементарного поворота тела, численно равный d φ и направленный вдоль оси вращения ОО ' так, чтобы, глядя вдоль вектора, мы видели вращение по часовой стрелке (направление вектора
– вектор элементарного поворота тела, численно равный d φ и направленный вдоль оси вращения ОО ' так, чтобы, глядя вдоль вектора, мы видели вращение по часовой стрелке (направление вектора 
 , численно равный первой производной от угла поворота по времени и направленный вдоль оси вращения в направлении
, численно равный первой производной от угла поворота по времени и направленный вдоль оси вращения в направлении  .
.
 .
.
 .
.  ортогонален к векторам
ортогонален к векторам  .
. ,
,  ,
,  .
. для характеристики неравномерного вращения тела:
для характеристики неравномерного вращения тела: .
.
 направлен в ту же сторону, что и
направлен в ту же сторону, что и  , а
, а  направлен в противоположную сторону при замедленном вращении
направлен в противоположную сторону при замедленном вращении 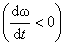 (рис. 2.13).
(рис. 2.13).


 .
.


 (3.19)
(3.19)







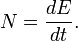

 — скалярная физическая величина, характеризующая способность материальной точки (тела) совершать работу за счет своего нахождения в поле действия консервативных сил. Другое определение: потенциальная энергия — это функция координат, являющаяся слагаемым в лагранжиане системы, и описывающая взаимодействие элементов системы
— скалярная физическая величина, характеризующая способность материальной точки (тела) совершать работу за счет своего нахождения в поле действия консервативных сил. Другое определение: потенциальная энергия — это функция координат, являющаяся слагаемым в лагранжиане системы, и описывающая взаимодействие элементов системы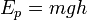 ,
, 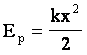








 и
и 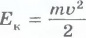 , можно закон сохранения механической энергии записать так:
, можно закон сохранения механической энергии записать так:


 некоторая точка, относительно которой мы будем находить момент вектора силы или вектора импульса. Ее (точку) называют началом или полюсом.
некоторая точка, относительно которой мы будем находить момент вектора силы или вектора импульса. Ее (точку) называют началом или полюсом.  – вектор, проведенный из полюса к точке приложения силы. Момент силы
– вектор, проведенный из полюса к точке приложения силы. Момент силы  относительно точки
относительно точки  .
. не изменится, если точку приложения силы
не изменится, если точку приложения силы  относительно точки
относительно точки  . Производная
. Производная  по времени будет выглядеть так:
по времени будет выглядеть так:  . Т.к.
. Т.к. 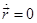 , а
, а  и мы получим
и мы получим 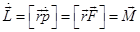 , т.е.
, т.е. 
 – производная момента импульса системы материальных точек по времени относительно неподвижного полюса равна геометрической сумме моментов всех внешних сил относительно того же полюса.
– производная момента импульса системы материальных точек по времени относительно неподвижного полюса равна геометрической сумме моментов всех внешних сил относительно того же полюса.


