Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Движение твёрдого тела вокруг неподвижной точки.Содержание книги
Поиск на нашем сайте
а). Это наиболее сложное вращение твёрдого тела. Существует приём описания такого движения: в каждый момент времени вращения Т.Т. вокруг неподвижной точки рассматривают, как вращение вокруг неподвижной мгновенной оси вращения; отсюда для каждой заданной радиус-вектором точки Т.Т. можно определить ск-ть, используя старые формулы, т.е. Задача: определить ск-ти М.Т. Т.Т., определив угловую ск-ть и зная координаты М.Т. Точка О – это полюс, относительно которого мы определяем положение произвольной м. точки. Полюс вводится для определения начала скользящего вектора. За dt т. М повернётся на
т.е. надо знать проекцию угловой ск-ти на оси выбранной СО. б). Задача: найдём эти проекции.
Т. О=О´, вокруг неё и происходит вращение твёрдого тела, которое мы заменяем вращением подвижной СО. Пусть Разложим вектор
Найдём ωx= ω1x+ ω2x+ ω3x. Найдём проекцию ωx, в конечном итоге выразим через кинематическое уравнение движения, которое в данном случае представлено уравнениями ψ=ψ(t), φ=φ(t), Θ=Θ(t). Т.к. случай вращения твёрдого тела вокруг мгновенной оси – это случай движения твёрдого тела с тремя степенями свобод (см. ранее). в)Проецируем
а) ω1x=0 (угол прямой); б) ω2x= в) ω3x= ωx= Получили проекцию ωx, выраженную через функции кинематических уравнений. Аналогично получаем для других проекций. В зависимости от СО получим разные ωx, но они все выражены через кинематические уравнения движения тела. Вывод: зная ωx, как функцию ωx=f(ψ,φ,Θ) и другие проекции можно получить выражение для Vx, как Vx=f(x,y,z,ψ,φ,Θ) – так решается кинематическая задача описания вращения твёрдого тела вокруг неподвижной точки. Момент инерции. 1). В общем случае при изучении движения важное значение имеет распределение массы, а не просто масса твёрдого тела. Только при поступательном движении достаточной характеристикой является масса твёрдого тела в целом. Инертнее свойства твёрдого тела связанные с распределением массы твёрдого тела описываются новой физической величиной (новой характеристикой) – моментом инерции. Она определяется относительно оси, которую мы выбираем. Момент инерции определяется так:
2). Вводят моменты инерции относительно осей декартовой СО.
У этих моментов инерции есть св-ва: г) А´+B´–C´
3). Теорема Штейнера. а). Теорема связывает момент инерции относительно произвольной оси с моментом инерции оси при параллельном переносе оси, проходящей через центр масс.
Оси S и C – параллельны. б).По определению момента инерции относительно оси S
Задача: сравнить моменты инерции относительно наших 2х осей:
И определим момент инерции
в). Используя определение и выражение для
32. Зависимость момента инерции от направления оси. 1). Момент импульса твёрдого тела сильно зависит от направления оси, т.е.
Положение S задаётся положением единичного вектора
2). Построим момент инерции. Выразим ρ, что самое трудное.
3). Выполним возведение в степень, систематизацию выражений. Подставим выражение в определение момента инерции, ведём обозначения моментов инерции относительно осей СО и центробежных моментов инерции.
Вывод: из формулы очевидно, что Is момент инерции относительно выбранной оси зависит от α, β и γ, причём зависимость эта достаточно сложная. α, β и γ-const. 4). Итак получили ур-е, к-е определяет изменение момента инерции Т.Т. в зависимости от положения α, β и γ оси вращения. Это ур-е сложное. Коэффициентами явл. моменты инерции относительно осей СО и центробежные моменты инерции, т.е. мы решили задачу определения
При изменении СО меняются коэффициенты Объекты, к-е характеризуют св-ва тела и так изменяются при изменении СО получили название тензоров. Они задаются матрицей
можно создать образ тензора инерции, построив эллипсоид инерции (поверхности), заданный ур-ем:
Получим уравнение эллипсоида (геометрия), но для нас это эллипсоид инерции – геометрическая интерпретация. Преобразованием (поворотом) осей СО можно получить форму уравнения эллипсоида:
А, В, С называют главным моментом инерции; в этом случае оси СО совпадают с осями симметрии эллипсоида. В этом случае момент инерции вычисляется проще всего. Вывод: момент инерции более сложная характеристика инертных св-в, чем масса. 33.Принцип виртуальных перемещений. 1. В аналитической механике рассматривается самый общий случай движения механической системы при наличии связи обычно это система материальных точек. Если эта система n точек с m связями, то S=3n–m – число степеней, то есть число независимых параметров, описывающих движение такой системы S. Пусть система из n точек находится в равновесии. Это значит, что силы, действующие на каждую точку равны нулю. Но это значит и следующее:
Если учесть, что силы могут быть заданные и связи, то получаем:
– уравнение для всей системы точек. Если связи идеальные, то:
– определение идеальных связей. В координатном представлении получаем:
– принцип аналитической статики – принцип виртуальных перемещений. 2. В 1770 г. Бернулли, Лагранж и Гамильтон. анализ. Если связей нет, то В этом случае условия равновесия:
В случае наличия связей, то есть для несвободной системы вариации не являются независимыми величинами. В этом случае так получить уравнение равновесия нельзя. Необходимо перейти к независимым параметрам, то есть обобщить принцип виртуальных перемещений. 3. Рассмотрим для этого метод обобщённых координат. Суть его состоит в том, что от зависимых параметров (где i = 1.. n), переходим к
Подставим в уравнение принципа виртуальных перемещений:
Обобщённый принцип виртуальных перемещений будет выглядеть так:
|
||||
|
Последнее изменение этой страницы: 2016-04-18; просмотров: 247; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.219.13.244 (0.007 с.) |

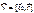 , где
, где 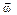 - мгновенная угловая скорость
- мгновенная угловая скорость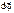 или на перемещение
или на перемещение 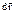 .
.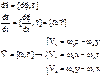
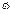 - мгновенная ось вращения, этот вектор проходит через т.О.
- мгновенная ось вращения, этот вектор проходит через т.О.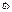 по трём неколлинеарным и некомпланарным направлениям:
по трём неколлинеарным и некомпланарным направлениям: , выбор направлений из соображения удобства.
, выбор направлений из соображения удобства.
 на оси:
на оси:
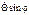
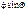 +
+ 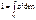

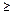 0.
0.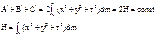 H – момент инерции относительно полюса центра СО (Н=const).
H – момент инерции относительно полюса центра СО (Н=const).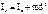 , где d – расстояние между осями.
, где d – расстояние между осями. . Раз оси разные, то момент инерции относительно осей разные.
. Раз оси разные, то момент инерции относительно осей разные.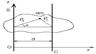 По теореме косинусов имеем:
По теореме косинусов имеем: 

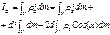
 (
(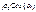 - координата dm, т.е. х
- координата dm, т.е. х 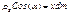 )получим:
)получим: момент инерции относительно оси ч/з центр масс всегда наименьше.
момент инерции относительно оси ч/з центр масс всегда наименьше.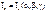 .
.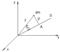 Покажем это.
Покажем это.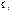 или cos(α), cos(β), cos(γ).
или cos(α), cos(β), cos(γ). 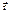 – местоположение момента dm.
– местоположение момента dm.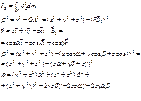 Заметим, что α, β, γ – определяют положение оси и для данного случая постоянны.
Заметим, что α, β, γ – определяют положение оси и для данного случая постоянны.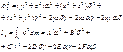
 – имеют смысл моментов инерции, поэтому получили название центробежных моментов инерции.
– имеют смысл моментов инерции, поэтому получили название центробежных моментов инерции.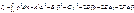
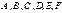 по определённым правилам. Они задаются линейными однозначными ур-ми. Напомним, что
по определённым правилам. Они задаются линейными однозначными ур-ми. Напомним, что 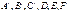 характеризуют инертные св-ва тела, все вместе.
характеризуют инертные св-ва тела, все вместе.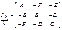
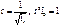 . с учётом, что x = к·α; y=r·β; z=r·γ:
. с учётом, что x = к·α; y=r·β; z=r·γ: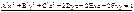
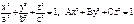 ; А, B, C – относительно нового положения осей.
; А, B, C – относительно нового положения осей.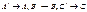
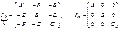
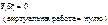 ;
; 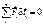
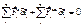
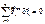

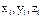 – независимые параметры.
– независимые параметры.
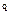 (где j = 1.. S), то есть
(где j = 1.. S), то есть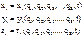 Между зависимыми и независимыми характеристиками системы осуществляется связь:
Между зависимыми и независимыми характеристиками системы осуществляется связь: