
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Классическая механика как теория механического движения макроскопических систем. Границы её применимости. Классическое представление о пространстве и времени.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Классическая механика как теория механического движения макроскопических систем. Границы её применимости. Классическое представление о пространстве и времени. 1. Объекты изучения. Классическая механика изучает движение макроскопических тел. За них принимают материальные объекты от атомов до звёзд. У них есть общее – изменение положения в пространстве с течением времени. Такое движение фундаментально в природе, в принципе оно определяет все другие физические явления (обусловленные движением). 2. Предмет (классическая механика)… Классическая механика – система знаний, в принципе наука. Отсюда её предмет – знание, но особое от других механик, отличающееся более строгим использованием математических моделей (но в том числе и физических моделей). Какие знания изучает классическая механика: а) модели объектов природы – фундамент из них материальная точка (МТ); б) принципы – относительности, дальнодействия, как механизма взаимодействия, симметрии, дополнимости, соответствия; в) понятия и физические величины – основные средства описания объектов и явлений;
г) законом и вершиной является система знаний – теория; 3. Теория. а) Теория – это замкнутая система понятий, объясняющая явления данной области; б) Её структура:
Классические представления о пространстве и времени. 1. Пространство и время в механике не зависят от движения тел – их существование, фундаментальное свойство нашего мира. 2. В механике Ньютона постулируется абсолютность пространства и времени, кроме того, пространство считается непрерывным, однородным, изотропным – евклидовым; время – непрерывно, однородно, однонаправлено. Свойства пространства и времени получают цифровое выражение, говорят об их арифметизации. Эталоны длинны и времени. Границы применимости. а) Всей механики – в новых объектах изучения (микрочастицы, поля, релятивистское движение); б) классическая механика материальной точки – только для данной модели, для малых скоростей, в инерциальных системах отсчёта (ИСО), для малых взаимодействий 2. Уравнения движения. 1. Элементарное механическое событие – это нахождение материальной точки в точке пространства с XYZ в момент t. . Механическим движением называют непрерывную совокупность элементарных механических событий. Для описания механического движения надо иметь систему отсчета. Проблема синхронизации часов в механике решается легко- мгновенный сигнал (дальнодействие) позволяет это делать автоматически.
при движении положение м.т. с течением времени изменяется т.е. 4 в декартовой со положение м.т. определяется тройкой чисел (х,у,z), говорят,чтосвободная м. т. имеет три степени свободы. В этой с о эти Ур дв имеют вид x=x(t) y=y(t) z=z(t). Эти Ур дают и траекторию дв с учетом св- в пространства выбраны и св-ва Ур, они непрерывны, дифференцируемы.. 5. Но удобно использовать полярную систему отсчёта.
ее связь с дек сов случае плоского дв. Простая
От одной системы отсчёта и уравнений, можно перейти к другой. x=x(q1, q2, q3)=f(t) y=y(q1, q2, q3)=f(t) – функция времени. z=z(q1, q2, q3)=f(t) (q1, q2, q3 - обобщённые координаты). 6. Достаточно распространённым является естественный способ движения материальной точки. Он выражается: а) задаётся траектория; б) определяется закон движения по траектории S=S(t). Динамика материальной точки. Основные понятия и законы 1. В науке недостаточно внешнего писания явлений, она вскрывает причины. Единственной причиной механического движения -механич.взаимодействие макроскопических тел на расстоянии и соприкосновении. По природе это гравитационные и электромагнитные взаимодействия. Принцип независимости взаимодействий: материальные причины взаимосвязи не могут зависеть от логики, цели, исчезать и появляться по желанию. 2. Основными понятиями являются: а) Ускорение материальной точки, сила, как характеристика действия, масса, как характеристика инертности. В механике 2 взаимодействия тел: появление ускорений; деформация тел С учетом явления и цели изучения строят модели тела, гениальная – материальная точка. 3. Законы динамики (Ньютона) 1. изолированная МТ находится в покое или равномерном прямолинейном движении (СО в которых это так называют ИСО) 2. ускорение МТ совпадает по направлению с направлением силы, прямо-пропорционально ей, обратно-пропорционально массе. 3. силы, с которыми действуют друг на друга 2 взаимодействующие МТ равны по величине, противоположны по направлениям. 4. Принцип суперпозиции сил:
если на МТ действует n сил, то каждая сила приводит к ускорению а1,..аn, которые в конечном итоге приводят к движению тела с ускорением а, это движение приводимой силы F. 3. Для описания мех.движения вводится система отсчета, наиболее простая – ИСО. В ИСО причиной ускоренного движения явл-ся материальное действие, т.е. реализуется механический детерменизм. Механическая эквивалентность ИСО фиксируется в принципе относительности Галилея:
По принципу независимости действий сила – инвариант, на основе 2 з-на Ньютона масса – инвариант. Роль начальных условий. 1. Получается, что силы однозначно не определяют движение материальной точки. Однозначность решения определяется дополнительными условиями, которые называются начальными, это координаты и скорость в начальный момент времени при t=0.
2. Из этой системы выражающей начальные условия можно получить значения наших неопределённых постоянных.
Имеем право сейчас эти постоянные подставить в общее решение и получить уже частное решение в виде:
Эти кинематические уравнения описывают тот случай движения, который у нас действительно происходит. Принцип причинности. Если заданы силы и начальные условия, то в механике с помощью основного Ур-я можно предсказать состояние системы в любой момент прошлого и будущего. Эта идея получила название механический детерминизм. 1) возникает проблема с точностью определения начальных условий 2) в этой модели невозможно учесть действие случайных сил 3) модель не работает для большого числа частиц и в микромире. Это ограничивает строгий детерминизм. Понятие связи. 1. Разнообразных материальных связей (взаимодействий) м/у телами очень много. Одни действия на тело м. описать силами, другие – трудно, а в теории - невозможно Связи – объективные условия (действия), ограничивающие движение тела (на языке моделей МТ). 2. Классификация связей. а) Удерживающая б) Неудерживающая в) Стационарная связь г) Нестационарная д) Неголономная связь е) Голономная связь
Наложение связи уменьшает число степеней свободы материальной точки на единицу, так как само уравнение связи устанавливает некую взаимосвязь (x,y,z), оставляет независимыми только две координаты. Если на материальную точку накладывается две связи заданные в виде уравнений поверхностей
Различают идеальные и неидеальные связи по принципу – работа идеальных связей равна нулю. Связь накладывает ограничения и на скорость материальной точки.
эта формула показывает, что Принцип относительности. 1. В кинематике материальной точки нет принципиального различия между инерциальными и неинерциальными системами отсчёта. Различие систем отсчёта выражается лишь в формальной сложности уравнений, что не принципиально. 1. В динамике различия между системами отсчёта может быть принципиальным, в частности не во всех системах отсчёта выполняется великий закон 3. Оказывается, существуют такие системы отсчёта, в которых Такие системы отсчёта называют инерциальными, они друг относительно друга двигаются прямолинейно и равномерно. Для них
Классический принцип относительности выражается в инвариантности законов Ньютона, относительно преобразований Галилея. Силы инерции. 1. В случае НИСО, появляются ускорения, к-е нельзя объяснить действием матер. тел – это св-во системы. Ускорения, обусловленные самой системой отсчета сводятся к апер и акар. Вот и получаем
2. Выражениям скобкам может быть приписан смысл силы, их стали называть силами инерции.
Для общего случая при наличии связи имеем уравнение
3. Для случая покоя материальной точки в такой системе отсчёта получаем
Основное уравнение МТ в НИСО
Получаем уравнение: 2. Если связей нет, то r=0 и уравнение будет:
2. Если система отсчёта равномерно вращается (наша Земля), а МТ без связи, но движется, то:
Угловое ускорение: Принцип эквивалентности. 1. Принцип эквивалентности яв-ся обобщением опыта изучения и описания движений тел в разных СО. Он утверждает, что mr =kmr Локальное гравитационное поле равнозначно существованию НИСО, специально выбранных. Если локально-гравитационное поле эквивалентно поступательно и ускоренно движущейся СО, то тогда Ур-е движения МТ с одной стороны – в ИСО в гравитационном поле, с другой стороны – в НИСО без гравитационного поля должны иметь одинаковый вид. а) В ИСО при наличии поля имеем:
б) В НИСО поля нет (СО движется прямолинейно, равноускоренно, то МТ в СО покоится, но на нее действуют силы)
Его легко м. подобрать, чтобы было: Вывод: подбором НИСО м. создать ситуацию (локальную), когда ур-е движения МТ будет равносильно Ур-ю движения МТ в ИСО в гравитационном поле. Работа силы. а) Определение. Для постоянной силы работа определяется Работа физическая величина, единица измерения [Дж], прямого измерения нет, характеризует действие на перемещении. б) Для элементарной работы существует определение:
Оказывается в общем случае правая часть, а значит и элементарная работа не является полным дифференциалом какой-либо функции. в) В интегральном виде для работы получаем
При преобразовании подынтегрального выражения пределы интегрирования может быть и по времени от Потенциальные силы. а) Определение. Потенциальной силой называют силу, которая удовлетворяет условию б) доказательство потенциальности силы может быть разное, в частности опирается на правило
в) Стационарное поле. Сила зависит от времени. СТАЦИОН-Я СИЛА-сила, к-я не зависит от времени.
элементарная работа для такой является дифференциалом функции При интегрировании получаем:
Видно, сто потенциальная энергия в точке зависит от выбора точки отсчёта, от выбора нулевой потенциальной энергии (нормировано), нет однозначности в определении U. Изменяемая лишь разность потенциальных энергий, т.е. работа. г) При определении потенциальности силы удобно использовать
если производная силы опред-ся так, то сила потенциальна. Нестационарная сила- большой класс сил, к-е зависят от времени.
В случае такой силы, у нас работу уже не выражается через разность потенциальной энергии; её расчёт более сложен. Силы инерции. 3. В случае НИСО, появляются ускорения, к-е нельзя объяснить действием матер. тел – это св-во системы. Ускорения, обусловленные самой системой отсчета сводятся к апер и акар. Вот и получаем
2. Выражениям скобкам может быть приписан смысл силы, их стали называть силами инерции.
Для общего случая при наличии связи имеем уравнение
3. Для случая покоя материальной точки в такой системе отсчёта получаем
Основное уравнение МТ в НИСО
Получаем уравнение: 2. Если связей нет, то r=0 и уравнение будет:
4. Если система отсчёта равномерно вращается (наша Земля), а МТ без связи, но движется, то:
Угловое ускорение: Принцип эквивалентности. 1. Принцип эквивалентности яв-ся обобщением опыта изучения и описания движений тел в разных СО. Он утверждает, что mr =kmr Локальное гравитационное поле равнозначно существованию НИСО, специально выбранных. Если локально-гравитационное поле эквивалентно поступательно и ускоренно движущейся СО, то тогда Ур-е движения МТ с одной стороны – в ИСО в гравитационном поле, с другой стороны – в НИСО без гравитационного поля должны иметь одинаковый вид. а) В ИСО при наличии поля имеем:
б) В НИСО поля нет (СО движется прямолинейно, равноускоренно, то МТ в СО покоится, но на нее действуют силы)
Вывод: подбором НИСО м. создать ситуацию (локальную), когда ур-е движения МТ будет равносильно Ур-ю движения МТ в ИСО в гравитационном поле.
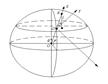
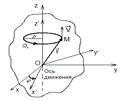
1. Земля - неинерциальная система отсчёта с постоянной скоростью вращения. Равновесие материальной точки (и любой системы материальных точек) важный случай механических явлений на Земле. Если точка покоится, то, значит, действует связь и в общем виде уравнение движения таково:
2. Решим его. На материальную точку действует (см. рис.) две силы Очевидно, на материальную точку действует третья сила – сила реакции опоры, вместе три силы компенсируются, и создаётся условие равновесия. По определению 3. Задача: в целом получается, что уравнение, описывающее движение материальной точки будет равно 1. Задача – определение угла отклонения отвесной линии. Отвесной линией называется линия, по которой располагается тяга материальной точки на нить (математический маятник).
1) Этот 2) 4. Метод определения
(где
5. Задача. Определить, как меняется g с широтой места Геометрический метод решения
Если взять точку на полюсе, то На полюсе радиус вращения материальной точки равен 0, т.е.
б) max на полюсе. Свободное падение МТ в условиях Земли. 1) МТ с высоты Н свободно падает без начальной скорости, значит на нее действует Fг, Iпер.цс., Iкар 2) Основное ур-е: 3) Его решение д.б. последовательным: выбор осей СО, получение ДУ, их решение с учетом начальных условий. 28. Описание движения твёрдого тела. Число степеней свободы. Координаты твёрдого тела. Кинематические уравнения движения. Углы Эйлера. Описание движения твёрдого тела. Проблема описания движения. 1. Твёрдое тело – это модель тела; обычно называют абсолютно твёрдое тело. Абсолютно твёрдое тело – называют неизменную систему м. точек, расстояния между которыми постоянно. 2. Число степеней свободы твёрдого тела. У одной м. точки – три степени свободы или три независимых координаты. Это значит, что для описания её положения необходимо задать три уравнения движения.
Для двух м. точек необходимо задать уже пять уравнений движения: (x2–x1)2+(y2–y1)2+(z2–z1)2=l2
Для трёх точек шесть уравнений движения: Для четырёх точек тоже шесть уравнений движения, т.е. тоже 6 степеней свободы. Вывод: абсолютно твёрдое тело с N точками с составе имеет шесть степеней свободы; для его описания необходимо шесть уравнений движения. 3. Выбор независимых координат для описания твёрдого тела.
Свяжем с абсолютно твёрдым телом ещё одну систему координат. X´Y´Z´ - жестко связана с твёрдым телом и вместе с ним движется.
Задача состоит в том, чтоб описать в неподвижной СО поведение подвижной СО; описание движения подвижной СО равносильно описанию твёрдого тела. Надо выбрать шесть независимых параметров. а) Три параметра – это положение подвижной СО т. О´, т.е. x0, y0, z0. б) Остальные три параметра должны описывать вращение подвижной СО, т.е. изменение осей подвижной СО. Выберем эти три параметра, связанные с вращением. Девять направляющих косинусов задают положение оси, но они не независимы. Рациональный выбор независимых координат, связанных с вращением подвижной СО был сделан Эйлером. Плоскость X´OY´ пересекает плоскость XOY по линии N. ψ – угол прецессии; φ – угол вращения; Θ – угол нутаии. Маятник Фуко. 1. Это типичная задача описания дв-я МТ в конкретной НИСО (земля). Она имеет ситорическое значение: в ней предсказывается, что плоскость качания маятника дв-ся, вращается (1850, Фуко). Решение и опыт док-ли неинерциальность системы Земля. 2. Постановка задачи.
3.Определим проекции нужных векторов на оси., и одновременно запишем само основное уравнение маятника. а)
б)
4. Строим дифф-е ур-я дв-я, проектируя основное уравнение на оси.
5. Упростим сист. ДУ. а) При малости
б) 6. Для решения полученной системы перейдем в новую СО- полярную.(для удобства). Используем искусств прием:
надо подчеркнутые выр-я изменить, увидев в них производные какой-то ф-и.
перейдём к полярной системе
Виды движения. 1). Поступательное движение – это такое движение Т.Т, при котором любая прямая, проведённая в твёрдом теле перемещается параллельно самой себе. При этом траектории точек Т.Т. могут быть сами разными. Получается, что вращательного движения твёрдого тела нет, значит, ψ, φ, Θ - const. Раз точки прямой по определению движутся одинаково, то их движения будет описано, если описано движение одной точки, то есть известен
2). Вращение твёрдого тела вокруг неподвижной оси. а).Это такое движение, при котором в твёрдом теле можно провести прямую, точки которой имеют нулевую скорость. б). Совместим OZ с OZ´. Допустим, ось вращения совпадает с OZ. Выберем произвольную точку М, траектория её движения будет окружность, с радиусом ρ. Положение точки М задаётся радиусом вектором В случае только движения из трёх углов ψ, φ, Θ изменяется лишь один – угол φ, движение имеет одну степень свободы
Докажем, что · по определению
· Вектор Для определения скорости надо знать направление скорости.
То есть при наличии (известных) x, y, z – положение т. М, надо знать проекции угловой скорости на оси неподвижной СО. Момент инерции. 1). В общем случае при изучении движения важное значение имеет распределение массы, а не просто масса твёрдого тела. Только при поступательном движении достаточной характеристикой является масса твёрдого тела в целом. Инертнее свойства твёрдого тела связанные с распределением массы твёрдого тела описываются новой физической величиной (новой характеристикой) – моментом инерции. Она определяется относительно оси, которую мы выбираем. Момент инерции определяется так:
2). Вводят моменты инерции относительно осей декартовой СО.
У этих моментов инерции есть св-ва: г) А´+B´–C´
3). Теорема Штейнера. а). Теорема связывает момент инерции относительно произвольной оси с моментом инерции оси при параллельном переносе оси, проходящей через центр масс.
Оси S и C – параллельны. б).По определению момента инерции относительно оси S
Задача: сравнить моменты инерции относительно наших 2х осей:
И определим момент инерции
в). Используя определение и выражение для
32. Зависимость момента инерции от направления оси. 1). Момент импульса твёрдого тела сильно зависит от направления оси, т.е.
Положение S задаётся положением единичного вектора
2). Построим момент инерции. Выразим ρ, что самое трудное.
3). Выполним возведение в степень, систематизацию выражений. Подставим выражение в определение момента инерции, ведём обозначения моментов инерции относительно осей СО и центробежных моментов инерции.
Вывод: из формулы очевидно, что Is момент инерции относ
|
|||||||
|
Последнее изменение этой страницы: 2016-04-18; просмотров: 1059; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.117.74.47 (0.012 с.) |




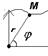
 2. Положение материальной точке в системе отсчёта (обычно выбирают простую, трехмерную, прямолинейную, ортогональную, декартовую с.о.) задается радиус-вектором
2. Положение материальной точке в системе отсчёта (обычно выбирают простую, трехмерную, прямолинейную, ортогональную, декартовую с.о.) задается радиус-вектором  ,где
,где  -единичные орты
-единичные орты  .
.

 - это средство описания мех. дв. – кинематический закон дв. При описании дв. В с.о. стремятся получить уравнения в самой элементарной форме, ч/з простейшее дв по осям х, у, z. x=x(t) y=y(t) z=z(t)-кинематическими уравнениями движения. зная их можно найти все другие ккинемат хар-ки дв
- это средство описания мех. дв. – кинематический закон дв. При описании дв. В с.о. стремятся получить уравнения в самой элементарной форме, ч/з простейшее дв по осям х, у, z. x=x(t) y=y(t) z=z(t)-кинематическими уравнениями движения. зная их можно найти все другие ккинемат хар-ки дв
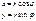





 Итак, получаем: t=0;
Итак, получаем: t=0; 

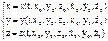
 ;
;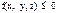 ;
;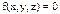 нет t (времени) – стационарная удерживающая связь;
нет t (времени) – стационарная удерживающая связь; ;
; - от скорости зависит;
- от скорости зависит;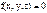 - от скорости зависит;
- от скорости зависит; - неудерживающая, нестационарная, неголономная связь.
- неудерживающая, нестационарная, неголономная связь.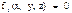 ,
, 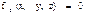 , то материальная точка имеет одну степень свободы, её движение осуществляется по кривой линии.
, то материальная точка имеет одну степень свободы, её движение осуществляется по кривой линии.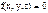

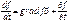
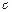 - вектор не может быть любым хотя бы по направлению.
- вектор не может быть любым хотя бы по направлению.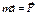 , не инвариантен при переходе из одной системы отсчёта в другую систему отсчёта, в частности мы доказали, что не инвариантно оказывается ускорение в разных системах отсчёта.
, не инвариантен при переходе из одной системы отсчёта в другую систему отсчёта, в частности мы доказали, что не инвариантно оказывается ускорение в разных системах отсчёта.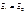 .
.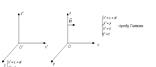 4. Переход из одной ИСО в другую управляется преобразованием Галилея, для простого случая:
4. Переход из одной ИСО в другую управляется преобразованием Галилея, для простого случая: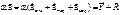 Þ по закону сложения ускорений при сложении движений материальной точки.
Þ по закону сложения ускорений при сложении движений материальной точки.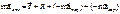
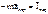 ,
, 
 - Основное уравнение динамики МТ в НИСО
- Основное уравнение динамики МТ в НИСО
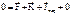

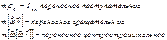
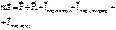
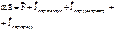
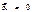
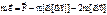 , при отсутствии связей свободное падение.
, при отсутствии связей свободное падение.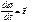
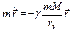 Гравитационная сила
Гравитационная сила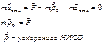
 =
= 
 , скалярное произведение векторов.
, скалярное произведение векторов. , где
, где  - элементарный вектор перемещения.
- элементарный вектор перемещения.

 до
до  , так задачи решают, рассчитывая работу.
, так задачи решают, рассчитывая работу. (u-СКАЛЯРНАЯ ФУНКЦИЯ.)и которая не зависит от скорости и
(u-СКАЛЯРНАЯ ФУНКЦИЯ.)и которая не зависит от скорости и 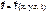
 , если
, если  .
.  , а, значит, проекции ротора на оси равны нулю, т.е.
, а, значит, проекции ротора на оси равны нулю, т.е. 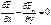 или
или  ;
;  и на другие оси подобные условия.
и на другие оси подобные условия. , тогда для работы имеем
, тогда для работы имеем
 .
. Т.е. работа не зависит от формы траектории, а определяется начальным и конечным положением.
Т.е. работа не зависит от формы траектории, а определяется начальным и конечным положением. , проинтегрируем:
, проинтегрируем:  ,
,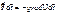


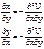
 Квазиупругая сила:
Квазиупругая сила:  .В общем случае имеем три подобных уравнения.
.В общем случае имеем три подобных уравнения.

 Þ по закону сложения ускорений при сложении движений материальной точки.
Þ по закону сложения ускорений при сложении движений материальной точки.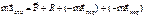
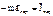
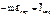
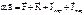 - Основное уравнение динамики МТ в НИСО
- Основное уравнение динамики МТ в НИСО
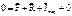

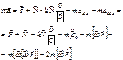
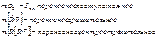
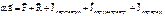

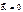
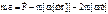 , при отсутствии связей свободное падение.
, при отсутствии связей свободное падение.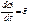
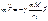 Гравитационная сила
Гравитационная сила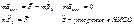
 Его легко м. подобрать, чтобы было:
Его легко м. подобрать, чтобы было: 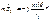

 26.Равновесие МТ на поверхности Земли.
26.Равновесие МТ на поверхности Земли.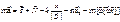 - это и есть уравнение равновесия.
- это и есть уравнение равновесия.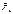 и
и  . Природа одной - действие Земли, природа второй – вращающаяся система отсчёта. Очевидно, что эти две силы не могут привести к равновесию материальной точки.
. Природа одной - действие Земли, природа второй – вращающаяся система отсчёта. Очевидно, что эти две силы не могут привести к равновесию материальной точки.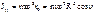 - по определению.
- по определению.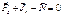 .
.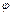 Эта линия вектора
Эта линия вектора 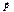 , значит надо знать угол
, значит надо знать угол 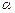 или угол.
или угол.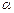 - мал;
- мал;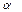 - зависит от положения материальной точки на поверхности Земли.
- зависит от положения материальной точки на поверхности Земли. - геометрически.
- геометрически.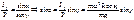
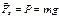 по определению).
по определению).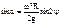 - это выражение позволяет определить
- это выражение позволяет определить 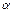 , если известно
, если известно 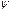 , т.е. положение точки на поверхности Земли, географическая широта (широта места).
, т.е. положение точки на поверхности Земли, географическая широта (широта места).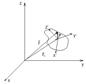 При известной
При известной 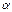 . Принимают при
. Принимают при 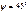 ,
, 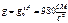 ,
, 
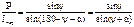
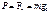 , g0 – на полюсе.
, g0 – на полюсе. .
.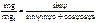
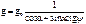 , При малых
, При малых 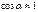 .
. а) ускорение свободного падения МТ зависит от положения МТ на поверхности Земли.
а) ускорение свободного падения МТ зависит от положения МТ на поверхности Земли.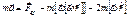
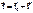
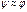 (ввиду малости)-географич-я широта. Угол отклонения маятника малый, т.е. колебания гармонические, в нач-й момент вр-ни маятник находится в центре СО.
(ввиду малости)-географич-я широта. Угол отклонения маятника малый, т.е. колебания гармонические, в нач-й момент вр-ни маятник находится в центре СО.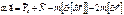 ,
, 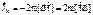


 -сила, действующая со стороны нити на МТ.
-сила, действующая со стороны нити на МТ.  .
. направлена вертикально вниз
направлена вертикально вниз 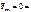
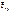 ,
, 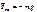
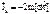
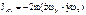
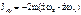
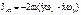
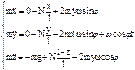 ,
, 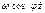 =0
=0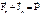 Эта система приближенно описывает движение матем маятника в системе Земля, но хорошо. Решается она приближенно при нек-х дополнительных упрощениях.
Эта система приближенно описывает движение матем маятника в системе Земля, но хорошо. Решается она приближенно при нек-х дополнительных упрощениях.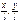 , тогда из условия
, тогда из условия 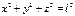 ,
, 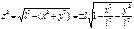 - величина второго порядка малости.
- величина второго порядка малости. 
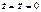
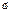 -по величине мала, тогда
-по величине мала, тогда 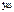 -пренебрегаем. Из 3-го ур-я имеем
-пренебрегаем. Из 3-го ур-я имеем 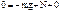 , N=mg. И неком приближении учтем это при изменении 1 и 2 ур-й.
, N=mg. И неком приближении учтем это при изменении 1 и 2 ур-й. 
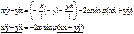
 ,
, 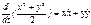
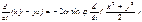
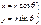
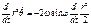 Интегрируем:
Интегрируем: 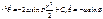 t=0, r=0 – начальное условие Þ С=0.
t=0, r=0 – начальное условие Þ С=0. 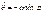 , т.е.
, т.е.  , Угол
, Угол 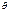 меняется с постоянной скоростью.
меняется с постоянной скоростью.  (скорость) и
(скорость) и  (географ-я широта)постоянные для данной земли и для данной точки местности, что означает, что плоскость колебания маятника вращается.
(географ-я широта)постоянные для данной земли и для данной точки местности, что означает, что плоскость колебания маятника вращается.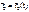 для т. О´.
для т. О´. В этом случае твёрдое тело имеет три степени свободы.
В этом случае твёрдое тело имеет три степени свободы.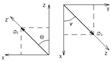 Для описания движения надо знать и скорости точек твёрдого тела, в данном случае, они находятся дифференцированием линейных уравнений движения.
Для описания движения надо знать и скорости точек твёрдого тела, в данном случае, они находятся дифференцированием линейных уравнений движения.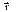 .
. Для характеристики вращения твёрдого тела (а значит и подвижной СО), вводят угловую скорость ω, как
Для характеристики вращения твёрдого тела (а значит и подвижной СО), вводят угловую скорость ω, как 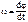 , и вводят вектор угловой скорости
, и вводят вектор угловой скорости  , модуль которого равен
, модуль которого равен 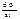 , а направление по оси вращения, по правилу буравчика (правого винта).
, а направление по оси вращения, по правилу буравчика (правого винта).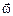 – вектор скользящий. У него нет фиксированного начала.
– вектор скользящий. У него нет фиксированного начала. .
. – касательная к траектории точки М. Её модуль V=ω·ρ, где ω – скорость вращения точки М.
– касательная к траектории точки М. Её модуль V=ω·ρ, где ω – скорость вращения точки М.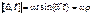
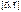 векторного произведения лежит перпендикулярно плоскости, образованной этими векторами. Этот вектор совпадает с направлением вектора
векторного произведения лежит перпендикулярно плоскости, образованной этими векторами. Этот вектор совпадает с направлением вектора 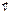 , что и требовалось доказать.
, что и требовалось доказать.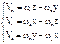
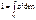

 0.
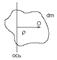
0.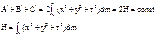 H – момент инерции относительно полюса центра СО (Н=const).
H – момент инерции относительно полюса центра СО (Н=const).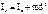 , где d – расстояние между осями.
, где d – расстояние между осями. . Раз оси разные, то момент инерции относительно осей разные.
. Раз оси разные, то момент инерции относительно осей разные.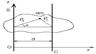 По теореме косинусов имеем:
По теореме косинусов имеем: 
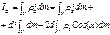
 (
(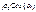 - координата dm, т.е. х
- координата dm, т.е. х 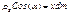 )получим:
)получим: момент инерции относительно оси ч/з центр масс всегда наименьше.
момент инерции относительно оси ч/з центр масс всегда наименьше.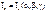 .
.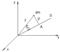 Покажем это.
Покажем это.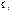 или cos(α), cos(β), cos(γ).
или cos(α), cos(β), cos(γ). 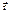 – местоположение момента dm.
– местоположение момента dm.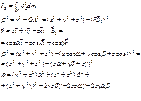 Заметим, что α, β, γ – определяют положение оси и для данного случая постоянны.
Заметим, что α, β, γ – определяют положение оси и для данного случая постоянны.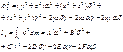
 – имеют смысл моментов инерции, поэтому получили название центробежных моментов инерции.
– имеют смысл моментов инерции, поэтому получили название центробежных моментов инерции.


