
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Кинематика поступательного движения.Содержание книги
Поиск на нашем сайте
КИНЕМАТИ Минимальный курс физики. Составлен доц. Юнусовым Н.Б.
ОГЛАВЛЕНИЕ. Стр.
Физика, ч.1. 2 (Физические основы механики. Механические колебания и волны. Молекулярная физика и термодинамика).
1.1. Основы кинематики. 2 1.2. Основы динамики. 4 1.3. Законы сохранения в механике. 6 1.4. Механика твердого тела. 8 1.5. Релятивистская динамика. 11 1.6. Механические колебания. 13 1.7. Механические волны. 16 1.8. Основы молекулярно-кинетической теории. 17 1.9. Функции распределения Максвелла и Больцмана. 20 1.10. Основы термодинамики. 21
Физика, ч.2. 29 (Электростатика. Электродинамика. Электромагнетизм. Электромагнитные колебания и волны).
2.1. Электрическое поле в вакууме. 29 2.2. Электрическое поле в веществе. 33 2.3. Электрический ток. 37 2.4. Магнитное поле в вакууме. 42 2.5. Магнитное поле в веществе. 49 2.6. Основы теории электромагнитного поля. 52 2.7. Электромагнитные колебания. 55 2.8. Электромагнитные волны. 57
Физика, ч.3. 58 (Волновая и квантовая оптика. Основы квантовой механики. Физика атома и твердого тела. Физика ядра и элементарных частиц).
3.1. Интерференция и дифракция света. 58 3.2. Поляризация и дисперсия света. 62 3.3. Тепловое излучение. 66 3.4. Фотоэффект. Эффект Комптона. Давление света. 68 3.5. Основные положения квантовой механики. 69 3.6. Квантовая теория атома. 74 3.7. Элементы физики твердого тела. 80 3.8. Ядро атома. 81 3.9. Элементарные частицы. 85 ФИЗИКА. Часть 1. ОСНОВЫ КИНЕМАТИКИ. Кинематика поступательного движения. Простейшая форма движения материи – механическое движение, т.е. изменение положения материальных тел в пространстве и во времени. Кинематика изучает движение тел без рассмотрения причин, его вызывающих. Простейшей физической моделью тела является материальная точка – тело, размерами которого в условиях данной задачи можно пренебречь. Для описания движения материальной точки необходима система отсчета: часы для отсчета времени и система координат (обычно выбирают прямоугольную декартову систему координат). Положение материальной точки в момент времени t определяется координатами х, у, z или радиус-вектором Мгновенная скорость материальной точки в момент времени t есть первая производная по времени от радиус-вектора движущейся материальной точки:
Вектор скорости в каждой точке траектории направлен по касательной к траектории в этой точке. Проекции вектора скорости на координатные оси х, у и z равны Характеристикой изменения скорости является ускорение В каждой точке траектории вектор ускорения можно разложить на две составляющие: одна из них направлена по касательной к траектории в данной точке и называется тангенциальным ускорением
Модуль полного ускорения равен Путь, пройденный за промежуток времени от момента t1 до t2,:
ОСНОВЫ ДИНАМИКИ. Законы динамики. В основе динамики лежат три закона Ньютона. Первый закон Ньютона (закон инерции) касается движения тел, не испытывающих внешних воздействий: всякое тело сохраняет состояние покоя или равномерного прямолинейного движения до тех пор, пока воздействие со стороны других тел не заставит его изменить это состояние. Системы отсчета, жестко связанные с такими (свободными) телами, называются инерциальными системами отсчета (ИСО). Для количественного описания воздействия тел друг на друга вводится понятие силы. Сила — векторная величина Сила Второй закон Ньютона утверждает, что быстрота изменения скорости движения тела (ускорение) пропорциональна приложенной силе и происходит по направлению той прямой, по которой эта сила действует: В механике масса – основная характеристика тела, показывающая его способность противостоять ускоряющим силам, т.е. масса характеризует инертность материального тела. Масса тела зависит от его размеров и природы вещества. В механике масса – величина скалярная, положительная, аддитивная и постоянная. В единицах СИ масса измеряется в килограммах (кг), а сила – в ньютонах (Н). Второму закону Ньютона можно придать другую форму, учитывая определение ускорения: Если ввести понятие импульса материальной точки Второй закон Ньютона является уравнением движения материальной точки. Решая его можно определить зависимость координат и скорости материальной точки от времени. При этом, помимо вида функции F(x,y,z,t), должны быть заданы начальные условия: положение и скорость частицы в начальный момент времени. Третий закон Ньютона указывает, что воздействие тел друг на друга носит характер взаимодействия: силы, с которыми действуют друг на друга взаимодействующие тела, равны по величине, противоположны по направлению и никогда не уравновешивают друг друга, так как приложены к разным телам:
Механическая работа. В механике характеристикой такого действия сил, которое вызывает перемещение тел, является работа. В случае, когда тело движется прямолинейно, а сила
В общем случае движения по криволинейной траектории весь путь 12 разбивается на малые участки dℓ, которым соответствуют векторы бесконечно малых перемещений
МЕХАНИКА ТВЕРДОГО ТЕЛА.
Кинетическая энергия вращения. Момент инерции материальной точки и тела относительно неподвижной оси. Пусть материальная точка массой m движется вокруг некоторой оси по окружности радиуса r со скоростью υ. Тогда кинетическую энергию точки с учетом связи линейной и угловой скоростей υ =ω·r можно записать так:
Моментом инерции тела относительно оси называется сумма моментов инерции элементов (материальных точек), из которых состоит тело: Момент инерции сплошного тела определяют интегрированием по всему объему (по всем материальным точкам): Если тело имеет плотность ρ, то последнее равенство можно представить в виде:
Момент инерции сплошного цилиндра массой т и радиуса основания R относительно оси, проходящей через центр масс цилиндра параллельно его образующей, рассчитанный по этой формуле, равен: Для сплошного шара массой т и радиуса R момент инерции относительно оси, проходящей через центр масс шара, равен: Момент инерции для стержня длиной ℓ и массой т относительно оси, проходящей через центр масс стержня перпендикулярно ему,: Момент инерции J тела характеризует, с одной стороны, инертные свойства тела при вращательном движении, а с другой стороны, распределение вещества в пространстве относительно оси. Момент инерции, так же как и масса тела, является аддитивной величиной. Если известен момент инерции Jo тела относительно оси, проходящей через центр масс тела, то можно найти его момент инерции относительно любой другой параллельной ей оси: J = J0 + m·d 2, где d – расстояние между осями. Последнее равенство выражает теорему Штейнера: момент инерции относительно любой оси вращения равен моменту инерции относительно параллельной оси, проходящей через центр масс, сложенному с произведением массы тела на квадрат расстояния центра масс тела от оси вращения. Из теоремы Штейнера очевидно, что всегда J>J0, т.е. минимальное значение момента инерции достигается для оси, проходящей через центр масс. Единицей момента инерции в системе СИ служит 1 кг·м2. Если тело катится, то кинетическая энергия такого тела определяется поступательным движением тела как целого и вращением относительно движущейся оси:
Динамика твердого тела Пусть на материальную точку действует сила Так как Это уравнение легко обобщить на твердое тело, еслипод
Формально все соотношения, описывающие динамику вращательного движения, можно получить из соответствующих соотношений динамики поступательного движения материальной точки, если в последних заменить массу тела на момент инерции, силу – на момент силы, импульс точки – на момент импульса тела, а линейные скорость и ускорение – на угловые скорость и ускорение. Из основного уравнения динамики для вращательного движения В основе закона сохранения момента импульса лежит свойство изотропности (равноправности всех направлений) пространства, которое проявляется в том, что физические свойства и законы движения замкнутой системы не зависят от выбора направлений осей координат инерциальных систем отсчета..
РЕЛЯТИВИСТСКАЯ ДИНАМИКА. В конце 19 века было показано, что классическая механика не применима к описанию движения тел с очень большими, близкими к скорости света, скоростями. Это позволяет делать теория, созданная А.Эйнштейном. Специальная теория относительности (СТО) или по другому релятивистская динамика опирается на два постулата: МЕХАНИЧЕСКИЕ КОЛЕБАНИЯ
Свободные (собственные) колебания –колебания, происходящие без внешних воздействий за счет первоначально полученной телом энергии. Рассмотрим горизонтальный пружинный маятник жесткостью k и массой m, помещенный в среду с коэффициентом сопротивления r, на который вдоль оси х действует переменная внешняя сила F(t), изменяющаяся со временем, например, по гармоническому закону F(t) = F0 · cosΩt с некоторой частотой Ω. Уравнение движения маятника:
где введены обозначения Проанализируем уравнение (2).
1. Свободные гармонические незатухающие колебания.
Его решением является гармоническая функция: в чем легко убедиться, подставив (4) в (3). В (4) xm, ω 0 и φ0 – постоянные величины. xm – амплитуда – величина, указывающая максимальное значение координаты х при отклонении от положения равновесия, ω 0 – собственная частота, аргумент косинуса Частота колебаний зависит только от свойств колеблющейся системы, но не от амплитуды, а амплитуда и начальная фаза колебаний определяются начальными условиями ее движения, выводящими систему из состояния покоя. Скорость колеблющейся частицы равна: Ускорение частицы при таком движении: Складывая кинетическую энергию с потенциальной, найдем полную энергию частицы, колеблющейся под действием упругой силы:
Т.о., полная энергия пропорциональна квадрату амплитуды колебаний. Кинетическая и потенциальная энергии изменяются со временем, как sin2(ω0·t + φ0) и cos2(ω0·t + φ0), так что когда одна из них увеличивается, другая – уменьшается, т.е. процесс колебаний связан с периодическим переходом энергии из потенциальной в кинетическую и обратно. Средние за период колебания значения потенциальной и кинетической энергии одинаковы и равны W/2. Т.о., если на тело действует сила, пропорциональная величине смещения частицы х и направленная в сторону, противоположную этому смещению (таковы, например, упругая сила, F=– k·x, действующая на пружинный маятник, или сила тяжести, действующая на математический или физический маятники), то оно совершает т.н. гармонические колебания (движение совершается по закону синуса или косинуса). Примечание: В механике обычно рассматривают колебания: – математического маятника с периодом – физического маятника с периодом – пружинного маятника с периодом
МЕХАНИЧЕСКИЕ ВОЛНЫ.
Явление распространения колебаний в пространстве называется волновым движением или волной. Уравнение волны выражает зависимость смещения Ψ колеблющейся точки, участвующей в волновом процессе, от ее координаты х и времени t. Волна называется продольной, если колебания частиц происходят вдоль линии распространения волны; если колебания частиц перпендикулярны к направлению распространения волны, то волна называется поперечной. Геометрическое место точек, до которых к некоторому моменту времени дошло колебание, называется фронтом волны. Можно также в среде выделить геометрическое место точек, колеблющихся в одинаковых фазах. Эта совокупность точек образует поверхность одинаковых фаз или волновую поверхность. Форма фронта волны определяет тип волн, например, у сферической волны фронт представляет собой сферу. Скорость распространения волны есть скорость распространения данной фазы (волновой поверхности). Ее называют фазовой скоростью υ волны. Расстояние, на которое определенная фаза колебания распространяется за один период Т колебания, называется длиной волны λ =υ· T. Простейшим видом волн является плоская волна. Колебания частиц среды в ней происходят в плоскостях, перпендикулярных к направлению распространения. Если колебания в каждой точке следуют гармоническому закону и происходят с одной частотой, то волна называется гармонической и монохроматической. Уравнение плоской волны, распространяющейся в положительном направлении оси х, имеет вид: где А(х) = A0·e-rx – амплитуда колебаний точек среды, расположенных на расстоянии x от источника колебаний (в среде без затухания А=А0= const). Так как ω =2π/ T, то: Здесь k=2π/λ=2π/ (υ· T)=2πν/υ=ω/υназывается волновым числом и является модулем волнового вектора Уравнение волны в виде (18) – одно из возможных решений общего дифференциального уравнения, описывающего распространение возмущения в среде. Это общее уравнение называется волновым уравнением. Его можно получить, взяв от функции Ψ вторые производные по х и t,: где учтено, что в данном случае производные являются частными и сделана замена Вещество вместе с волной не переносится. Частицы вещества только колеблются каждая около своего положения равновесия. Колебания передаются вдоль направления распространения волны, вместе с ними передается и их энергия. Для описания этого процесса вводят вектор плотности потока энергии (вектор Умова) Выделим на фронте плоской волны (рис.) единичную площадку S. Через единицу времени фронт сместится на расстояние, равное скорости распространения волны υ и займет положение S ’. Если в единице объема содержится энергия w (плотность энергии), то за единицу времени через сечение S ’= 1 пройдет вся энергия, заключенная в объеме между сечениями S и S ’, т. е. w·υ. Это и есть вектор Умова, если записать в векторной форме:
где ρ – плотность вещества среды; ω – частота колебаний, А0 – амплитуда колебаний. Откуда следует, что: . В самом общем случае энергия волны, заключенная в некотором объеме V, согласно (21), рассчитывается по формуле: ОСНОВЫ ТЕРМОДИНАМИКИ Термодинамика – учение о превращениях одного вида энергии в другой, о передаче энергии от тела к телу. Термодинамика изучает свойства макроскопических тел без рассмотрения их молекулярной структуры. Термодинамическая система (ТС) – макроскопические тела, которые могут обмениваться энергией как друг с другом, так и с внешней средой. Равновесное состояние ТС - состояние, при котором термодинамические параметры (давление, температура и объем) остаются постоянными сколь угодно долго при неизменных внешних условиях. Термодинамический процесс – изменение состояния ТС, характеризующееся изменением ее параметров. Состояние ТС характеризуют также внутренней энергией, которая равна сумме кинетических энергий беспорядочного движения всех молекул и потенциальных энергий взаимодействия молекул друг с другом. Система тел называется изолированной, или замкнутой, если нет обмена энергией с окружающей средой. Первое начало термодинамики Тела и системы могут обмениваться энергией друг с другом. Существует два вида обмена энергией. Это может быть работа, произведенная одним телом (системой) над другим телом (системой). Примером может служить перемещение тела или его частей под действием упругих, электрических или других сил. Другой способ обмена энергией – путем передачи энергии неупорядоченного, хаотического движения молекул. Тогда говорят о передаче тепла. Например, передача энергии от нагретого тела к холодному происходит за счет передачи кинетической энергии хаотически движущихся молекул одного тела хаотическому движению молекул другого тела. В обоих этих случаях изменяется внутренняя энергия U. Сказанное выше можно записать как: Δ U = Q + А’, где Q – энергия, поступающая в систему при теплообмене, а А’ – работа, совершаемая внешними телами над системой. Исторически принято это соотношение записывать как: Q = ΔU + А (18), где А = – А’ –работа, совершаемая самой системой. (18), представляющее собой закон сохранения энергии, получило название первого начала термодинамики: «Подведенное к телу количество теплоты идет на увеличение внутренней энергии тела и на работу, которую тело производит». Очень важно отметить различие между величинами U с одной стороны, и А и Q – с другой. Внутренняя энергия U – это функция состояния системы. Если в состоянии 1 внутренняя энергия равна U1, то что бы ни происходило с системой, какую бы работу она ни совершала, какие бы количества теплоты к ней ни подводились, если система вернулась в то же состояние 1 (т. е. процесс оказался круговым, совершен цикл), ее внутренняя энергия будет снова U1 (Δ U =0). В то же время Q и А – это только передаваемые телу или получаемые от тела порции энергии. Они связаны с передачей энергии, а не с каким-то запасом их в теле. Бессмысленно говорить о запасе работы в теле. И так же бессмысленно говорить о запасе теплоты в теле. Работа и теплота не являются функциями состояния тела. Переходя к бесконечно малым порциям энергии, запишем первое начало в дифференциальной форме: δQ = dU + δA. (19). Здесь специально даны разные обозначения бесконечно малых («d...» и «δ …»), чтобы отразить то обстоятельство, что U – функция состояния, a Q и А – нет. Адиабатический процесс Процесс без обмена теплотой с окружающей средой называется адиабатическим. Он может происходить, если газ (или другое тело) окружен абсолютно не проводящей тепло оболочкой или процесс происходит очень быстро, так что газ не успевает обменяться теплом с другими телами. При таких процессах первое начало термодинамики упрощается: δQ = 0; dU = – δА. (32). Это означает, что если над газом производить работу ( δ А < 0), то dU > 0. Внутренняя энергия газа возрастает, он нагревается. Если же газ расширяется, то он сам производит работу δ А > 0 за счет собственной внутренней энергии и dU < 0. В результате он охлаждается. Согласно (25): dU =ν · CV · dT. Дляδ А используем соотношение (20). Тогда выражение (32) для адиабатического процесса можно записать так:
Подставим сюда р из уравнения Клапейрона-Менделеева (4) иполучим:
Проинтегрируем последнее выражение для пределов изменения переменных от T 1 до T 2 и от V 1 до V 2 и введя обозначение а используя Т = p·V/(ν·R), получаем Соотношения (36-37) носят название уравнений Пуассона или адиабаты. γ – показатель адиабаты.
При любых других процессах (неизотермических и неадиабатических) всегда можно связь между р и V написать в виде (37), но γ уже не будет равна Ср/СV. В этих случаях процесс называется политропическим, а γ – показателем политропы. Можно сказать, что для изотермического (T =const) процесса γ = 1, для изобарического (р = const) γ = 0, для изохорического (V = const) γ = ∞. На рисунке б показаны различные процессы расширения газа: 1 – изотерма, 2 – адиабата, 3 – изохора, 4 – изобара, 5 – политропа. Процессы 2, 3 идут с охлаждением, а 4, 5 – с нагреванием газа. Необратимые процессы
Другой пример: пусть газ находится и слева и справа от теплопроводной перегородки, но температура слева выше, чем температура справа (рис. б). Молекулы обмениваются с перегородкой кинетической энергией, и постепенно температуры обеих частей выравниваются. Такой процесс передачи тепла всегда необратим. Самопроизвольно средняя кинетическая энергия молекул (т. е. температура) слева сама не поднимется за счет кинетической энергии молекул справа. Любой процесс, сопровождающийся трением, также необратим, так как при этом энергия упорядоченного движения переходит в энергию беспорядочного движения молекул, т. е. в теплоту. Энтропия Пусть с рабочим веществом совершаются циклы, при каждом из которых подводится от нагревателя Q1, отдается холодильнику Q2 и производится работа А = Q1 – Q2. Из (38) и (39) можно получить:
Величина Qi /Ti называется приведенной теплотой. Обозначим ее Δ Si. Из (40) следует, что сумма приведенных теплот при циклическом процессе равна нулю. Это означает, что, какой бы циклический процесс мы ни совершали, если мы вернулись в исходное состояние, некоторая величина S не меняется ( Δ S = 0). Следовательно, S – функция состояния. Она получила название энтропии. Таким образом, состояние определяется не только внутренней энергией U, но и энтропией S. Если процесс не циклический и тело переходит из состояния 1 в другое состояние 2, то Рассмотрим теплопередачу при контакте двух тел при температурах Т1 и Т2 (Т1 > Т2) в теплоизолированной системе. Теплота Q, передаваемая телом 1, равна теплоте Q, полученной телом 2. Однако, тело 1 отдает ее при температуре Т1 и В тепловой машине часть теплоты, взятой от нагревателя, преобразуется в работу, а другая часть должна быть передана холодильнику. Нагреватель охлаждается, а холодильник нагревается. С одной стороны, мы знаем, что при этом энтропия возрастает. С другой стороны, к.п.д. такой тепловой машины будет постепенно падать, так как
|
||||
|
Последнее изменение этой страницы: 2016-08-15; просмотров: 2008; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.139.70.69 (0.012 с.) |

 . Модуль и направление радиус-вектора определяются тремя его проекциями на оси координат:
. Модуль и направление радиус-вектора определяются тремя его проекциями на оси координат:  ,
,  , где
, где 
 ,
,  ,
, 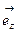 – единичные векторы направлений (орты).
– единичные векторы направлений (орты).  В процессе своего движения точка описывает некоторую линию, называемую траекторией. Расстояние, пройденное материальной точкой по траектории, представляет собой путь s. Вектор
В процессе своего движения точка описывает некоторую линию, называемую траекторией. Расстояние, пройденное материальной точкой по траектории, представляет собой путь s. Вектор  , соединяющий начальную и конечную точки траектории, называется перемещением. Зависимости координат материальной частицы x = x(t), y = y(t), z = z(t) или ее радиус-вектора
, соединяющий начальную и конечную точки траектории, называется перемещением. Зависимости координат материальной частицы x = x(t), y = y(t), z = z(t) или ее радиус-вектора 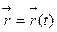 от времени называются кинематическими уравнениями движения.
от времени называются кинематическими уравнениями движения.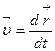 .
. ,
, 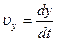 ,
,  , а вектор и модуль скорости определяются выражениями:
, а вектор и модуль скорости определяются выражениями:  и
и 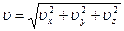 .
.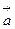 . В общем случае произвольного движения ускорение материальной точки в данный момент времени определяется как первая производная от вектора скорости (или вторая производная от радиус-вектора) по времени:
. В общем случае произвольного движения ускорение материальной точки в данный момент времени определяется как первая производная от вектора скорости (или вторая производная от радиус-вектора) по времени: 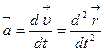 .
.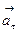 , другая – по нормали к траектории и называется нормальным, или центростремительным, ускорением
, другая – по нормали к траектории и называется нормальным, или центростремительным, ускорением  . Тангенциальное ускорение определяет изменение величины вектора скорости, а центростремительное ускорение – изменение его направления в данной точке траектории. Тангенциальное и нормальное ускорения определяются выражениями:
. Тангенциальное ускорение определяет изменение величины вектора скорости, а центростремительное ускорение – изменение его направления в данной точке траектории. Тангенциальное и нормальное ускорения определяются выражениями: ;
; 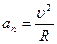 . R – радиус кривизны.
. R – радиус кривизны. , так как
, так как  .
. , где υ – модуль скорости.
, где υ – модуль скорости.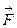 , которая определяется величиной или модулем F, направлениемв пространстве и точкой приложения. Если к материальной точке приложено несколько сил, их действие эквивалентно действию одной силы:
, которая определяется величиной или модулем F, направлениемв пространстве и точкой приложения. Если к материальной точке приложено несколько сил, их действие эквивалентно действию одной силы:  { принцип суперпозиции).
{ принцип суперпозиции).
 или
или  ;коэффициент пропорциональности т называется массой тела, а сила
;коэффициент пропорциональности т называется массой тела, а сила  или
или  .
. (это основная характеристика поступательного движения), товторой закон Ньютона принимает вид:
(это основная характеристика поступательного движения), товторой закон Ньютона принимает вид:  , т.е. быстрота изменения импульса тела равна силе, вызывающей это изменение.
, т.е. быстрота изменения импульса тела равна силе, вызывающей это изменение. .
.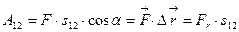
 Здесь Fr –проекция силы на направление перемещения, величина в круглых скобках – скалярное произведение силы
Здесь Fr –проекция силы на направление перемещения, величина в круглых скобках – скалярное произведение силы  . Работа представляет собой величину скалярную и алгебраическую. Если α < 900 , то работа A12 положительна. При α > 900 работа отрицательна. В случае, когда сила все время перпендикулярна перемещению (α = 900) (центростремительная сила), ее работа равна нулю.
. Работа представляет собой величину скалярную и алгебраическую. Если α < 900 , то работа A12 положительна. При α > 900 работа отрицательна. В случае, когда сила все время перпендикулярна перемещению (α = 900) (центростремительная сила), ее работа равна нулю. . Тогда на каждом таком участке силу можно считать постоянной и ее работу равной
. Тогда на каждом таком участке силу можно считать постоянной и ее работу равной  , а полная работа находится как сумма (интеграл) элементарных работ на участках dl, на которые разбивается участок 12,:
, а полная работа находится как сумма (интеграл) элементарных работ на участках dl, на которые разбивается участок 12,: .
.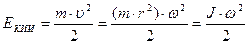 , где величина J=m·r2 называется моментом инерции материальной точки.
, где величина J=m·r2 называется моментом инерции материальной точки. .
. .
. , где учтено, что d т= ρ·dV.
, где учтено, что d т= ρ·dV. .
.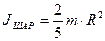 .
. .
. .
. .
.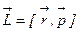 и
и  , то заменяя, получим основное уравнение динамики вращательного движения материальной точки:
, то заменяя, получим основное уравнение динамики вращательного движения материальной точки:  .
. и
и  понимать суммарный момент импульсов частиц
понимать суммарный момент импульсов частиц  , из которых состоит тело, и суммарный момент сил,
, из которых состоит тело, и суммарный момент сил,  , действующих на эти частицы. Приведем различные формы записи этого уравнения при неизменном моменте инерции (J=const):
, действующих на эти частицы. Приведем различные формы записи этого уравнения при неизменном моменте инерции (J=const): .
. для замкнутой системы (
для замкнутой системы ( ) следует закон сохранения момента импульса: в инерциальной системе отсчета момент импульса замкнутой системы частиц остается постоянным как по величине, так и по направлению, т.е.
) следует закон сохранения момента импульса: в инерциальной системе отсчета момент импульса замкнутой системы частиц остается постоянным как по величине, так и по направлению, т.е.  .
.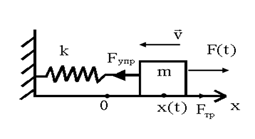 Движение, которое повторяется через равные промежутки времени, называется колебательным. Промежуток времени T, по истечение которого движение повторяется, называется периодом колебания. В моменты времени t и t + Т частица имеет одно и то же положение и одну и ту же скорость. Величина ν, обратная периоду, называется частотой: ν = 1/ Т. Она определяет, сколько раз в секунду повторяется движение, и измеряется в герцах (Гц). Круговой (циклической) частотой называется величина ω = 2 π v.
Движение, которое повторяется через равные промежутки времени, называется колебательным. Промежуток времени T, по истечение которого движение повторяется, называется периодом колебания. В моменты времени t и t + Т частица имеет одно и то же положение и одну и ту же скорость. Величина ν, обратная периоду, называется частотой: ν = 1/ Т. Она определяет, сколько раз в секунду повторяется движение, и измеряется в герцах (Гц). Круговой (циклической) частотой называется величина ω = 2 π v.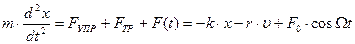 (1), где сила упругости FУПР пропорциональна смещению х, а сила трения (сопротивления) FТР среды – скорости υ= dx/dt. Перепишем (1) по другому:
(1), где сила упругости FУПР пропорциональна смещению х, а сила трения (сопротивления) FТР среды – скорости υ= dx/dt. Перепишем (1) по другому: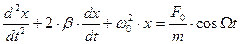 (2),
(2),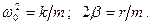
 Маятник в отсутствие силы трения (r =0) и внешней силы (F0= 0) отведен от положения равновесия и отпущен. Уравнение движения имеет вид:
Маятник в отсутствие силы трения (r =0) и внешней силы (F0= 0) отведен от положения равновесия и отпущен. Уравнение движения имеет вид: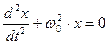 (3).
(3).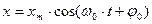 (4),
(4),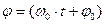 носит название фазы колебания; φ0 — начальная фаза колебания (в момент t = 0).
носит название фазы колебания; φ0 — начальная фаза колебания (в момент t = 0).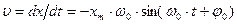 (5).
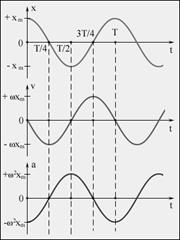
(5).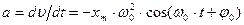 (6). На рис. приведены зависимости x(t), υ(t) и a(t) для φ0 =0.
(6). На рис. приведены зависимости x(t), υ(t) и a(t) для φ0 =0.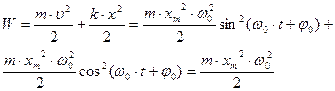 (7).
(7). , где ℓ– длина маятника;
, где ℓ– длина маятника; , где J– момент инерции маятника, a – расстояние от точки подвеса маятника до его центра масс;
, где J– момент инерции маятника, a – расстояние от точки подвеса маятника до его центра масс; , где k– жесткость пружины.
, где k– жесткость пружины.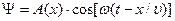 (17),
(17), (18).
(18). , указывающего направление распространения волны.
, указывающего направление распространения волны. (19),
(19), Выражение (19) справедливо для волн любой природы.
Выражение (19) справедливо для волн любой природы. , который направлен в сторону распространения волны, а его модуль равен энергии, переносимой волной через единицу площади за единицу времени.
, который направлен в сторону распространения волны, а его модуль равен энергии, переносимой волной через единицу площади за единицу времени. . Он измеряется в Дж/(с·м2) или, что то же самое, в Вт/м2. Эта формула справедлива не только для механических волн, но и для волн любой природы, например электромагнитных.
. Он измеряется в Дж/(с·м2) или, что то же самое, в Вт/м2. Эта формула справедлива не только для механических волн, но и для волн любой природы, например электромагнитных.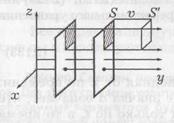 Объемную плотность энергии w упругой волны получим, если рассмотрим в какой-либо области пространства колебание частиц среды объемом dV и массой dm=ρ·dV. Полная энергия колебаний этих частиц, согласно (7), будет равна:
Объемную плотность энергии w упругой волны получим, если рассмотрим в какой-либо области пространства колебание частиц среды объемом dV и массой dm=ρ·dV. Полная энергия колебаний этих частиц, согласно (7), будет равна: (20),
(20),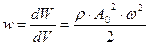 (Дж/м3) (21).
(Дж/м3) (21).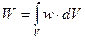 (22).
(22).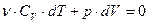 (33).
(33). ;
;  (34).
(34). (35). получим:
(35). получим: 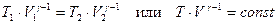 (36),
(36),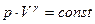 (37).
(37). Поскольку γ > 1, давление в (37) обратно пропорционально не V, как было при изотермическом процессе, а Vγ, т. е. давление убывает с увеличением объема быстрее. На рисунке a кривые 1 и 2 – изотермы (Т 2 < T 1), а кривая 3 – адиабата.
Поскольку γ > 1, давление в (37) обратно пропорционально не V, как было при изотермическом процессе, а Vγ, т. е. давление убывает с увеличением объема быстрее. На рисунке a кривые 1 и 2 – изотермы (Т 2 < T 1), а кривая 3 – адиабата. Рассмотрим процесс расширения газа. Пусть имеется сосуд с перегородкой (рис. а) в левой части которого есть газ, а в правой – нет. Уберем перегородку. Газ расширится и займет обе части. Если молекулы друг с другом не взаимодействуют (идеальный газ), то общая внутренняя энергия при таком процессе не изменится (UI =UII). Однако состояние II отличается от состояния I тем, что тело из состояния II самопроизвольно, без вмешательства извне не вернется в состояние I. Если молекул мало, например 2 или 3, то, двигаясь хаотически, случайно, они все могут в какой-то момент оказаться в левой части, но если молекул много, то это крайне маловероятно. Поэтому процесс расширения газа в пустоту называют необратимым.
Рассмотрим процесс расширения газа. Пусть имеется сосуд с перегородкой (рис. а) в левой части которого есть газ, а в правой – нет. Уберем перегородку. Газ расширится и займет обе части. Если молекулы друг с другом не взаимодействуют (идеальный газ), то общая внутренняя энергия при таком процессе не изменится (UI =UII). Однако состояние II отличается от состояния I тем, что тело из состояния II самопроизвольно, без вмешательства извне не вернется в состояние I. Если молекул мало, например 2 или 3, то, двигаясь хаотически, случайно, они все могут в какой-то момент оказаться в левой части, но если молекул много, то это крайне маловероятно. Поэтому процесс расширения газа в пустоту называют необратимым.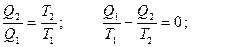 (40).
(40). . Когда тело получает теплоту (Q > 0), его энтропия возрастает, когда теряет (Q < 0) – энтропия уменьшается. При адиабатическом процессе (Q = 0) ΔS = 0 и S=const, поэтому адиабатический процесс называют еще изоэнтропийным.
. Когда тело получает теплоту (Q > 0), его энтропия возрастает, когда теряет (Q < 0) – энтропия уменьшается. При адиабатическом процессе (Q = 0) ΔS = 0 и S=const, поэтому адиабатический процесс называют еще изоэнтропийным. , а тело 2 получает ее при температуре Т2 и
, а тело 2 получает ее при температуре Т2 и  Так как Т1 > T2, следовательно, │Δ S 2│>│Δ S 1│, так что в целом при таком процессе энтропия возрастает. Т.о., при необратимых процессах энтропия увеличивается.
Так как Т1 > T2, следовательно, │Δ S 2│>│Δ S 1│, так что в целом при таком процессе энтропия возрастает. Т.о., при необратимых процессах энтропия увеличивается. и при Т1 → T2 к.п.д. η → 0. Общая энергия системы, включающей нагреватель, холодильник, рабочее вещество и тело, над которым производится работа, остается неизменной, но работы получается все меньше и меньше. В пределе, когда Т1 = T2, теплота от нагревателя не может быть использована вовсе. Тогда внутренняя энергия нагрев
и при Т1 → T2 к.п.д. η → 0. Общая энергия системы, включающей нагреватель, холодильник, рабочее вещество и тело, над которым производится работа, остается неизменной, но работы получается все меньше и меньше. В пределе, когда Т1 = T2, теплота от нагревателя не может быть использована вовсе. Тогда внутренняя энергия нагрев 


