
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Электродвижущая сила (э.д.с.)Содержание книги
Поиск на нашем сайте
Для того, чтобы в цепи шёл постоянный ток, цепь должна быть замкнута, и что-то в этой цепи должно постоянно генерировать электрическое поле. Это "что-то" и называется электродвижущей силой (э.д.с.) ε. Генерация поля (разности потенциалов на клеммах батареи на рисунке) осуществляется силами не электрической природы, например, за счёт химических реакций, продуктом которых является разделение зарядов, либо механическими и магнитными силами (гидро- и газогенераторы). Э.д.с. измеряется в вольтах, то есть это, по сути, не сила, а работа сторонних сил по перемещению единичного заряда против электрического поля (на рисунке положительные заряды внутри батареи должны быть перемещены от отрицательного контакта 1 к положительному 2, а во внешней цепи наоборот): Электрическое сопротивление Носители зарядов (электроны в металлах, ионы в электролитах) при своём движении сталкиваются с молекулами вещества проводника (с ионами кристаллической решётки в металлах, с другими ионами в электролитах). Направленное движение при этом замедляется – электрический ток испытывает сопротивление. Очевидно, что общее сопротивление R зависит от сечения проводника (чем оно больше, тем сопротивление меньше), от длины проводника (чем короче, тем сопротивление меньше), от вещества проводника. Если ввести так называемое удельное сопротивление ρ, зависящее только от материала, то можно записать для электрического сопротивления цилиндрического проводника: Закон Ома
I = Δφ / R. Если реальную электрическую цепь разомкнуть, то, естественно, ток по ней не пойдёт. Поэтому, когда говорят о законе Ома для незамкнутой цепи, имеют в виду, что из сложной электрической цепи, которая, разумеется, замкнута, и по которой идёт ток, мы выделяем незамкнутый участок и анализируем его отдельно от всей остальной цепи. При этом вклад всех остальных, не входящих в наш участок, э.д.с. мы учитываем в виде разности потенциалов на концах нашего участка цепи: Величину Записанная выше форма закона Ома для конечного участка цепи – замкнутого или незамкнутого называется интегральной – в противоположность дифференциальной, когда закон Ома записывается для любой точки проводника (точнее, для бесконечно малой окрестности этой точки). Формально получить закон Ома в дифференциальной форме очень просто. Сделав в законе Ома I = U/R подстановки: I=j·S; U=E·ℓ; R=ρ·ℓ/S, придем к искомой формуле:
где σ =1/ ρ – удельная проводимость вещества (Ом -1·м -1).
Т.о., сила тока I в проводнике пропорциональна напряжению U (закон Ома в интегральной форме) или плотность тока
Закон Джоуля-Ленца При постоянном токе в цепи электрическое поле совершает работу, в точности равную работе сил трения (сопротивления). Последняя полностью переходит в тепловую энергию Q проводника. Приравняв количество выделяемого в проводнике тепла Q работе поля по перемещению зарядов в цепи (А = q·U = I·t . U), получим закон Джоуля-Ленца в интегральной форме: Q = I·U·t=I2·R·t. Работа в единицу времени называется мощностью электрического тока: P = I·U=I2·R. Если использовать выражения: I=j·S; R=ρ·ℓ/S; V=S·ℓ и ввести понятие удельной тепловой мощности Pуд=Q / (V·t) (Дж / c·м3=Вт / м3), т.е. энергии, которая выделяется в единице объема проводника за единицу времени, то получим закон Джоуля-Ленца в дифференциальной форме: Pуд= ρ· j2= E2 / ρ=σ·E2.
|
||||
|
Последнее изменение этой страницы: 2016-08-15; просмотров: 678; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.188.245.152 (0.006 с.) |

 . За положительное направление тока в цепи принято направление движения положительных зарядов. Так, например, в металлических проводниках направление тока противоположно направлению движения носителей отрицательного заряда - электронов.
. За положительное направление тока в цепи принято направление движения положительных зарядов. Так, например, в металлических проводниках направление тока противоположно направлению движения носителей отрицательного заряда - электронов. где R – сопротивление (полное) (Ом); S – сечение проводника (м2); ℓ - длина проводника (м); ρ – удельное сопротивление (Ом·м) (приводится в справочниках). В самом общем случае, когда сечение и (или) удельное сопротивление проводника изменяются вдоль проводника, сопротивление рассчитывается как:
где R – сопротивление (полное) (Ом); S – сечение проводника (м2); ℓ - длина проводника (м); ρ – удельное сопротивление (Ом·м) (приводится в справочниках). В самом общем случае, когда сечение и (или) удельное сопротивление проводника изменяются вдоль проводника, сопротивление рассчитывается как:  .
. В 1826 г. Георг Ом экспериментально показал, что между силой тока в замкнутой цепи и разностью потенциалов Δφ на концах проводника существует простая связь:
В 1826 г. Георг Ом экспериментально показал, что между силой тока в замкнутой цепи и разностью потенциалов Δφ на концах проводника существует простая связь: .
. называют напряжением. Следует также отметить, что источник питания также имеет собственное сопротивление r, его называют внутренним сопротивлением э.д.с.. Обычно его делают малым по сравнению с внешним сопротивлением. Тем не менее, в общем случае внутреннее сопротивление r также нужно учитывать в законе Ома:
называют напряжением. Следует также отметить, что источник питания также имеет собственное сопротивление r, его называют внутренним сопротивлением э.д.с.. Обычно его делают малым по сравнению с внешним сопротивлением. Тем не менее, в общем случае внутреннее сопротивление r также нужно учитывать в законе Ома:  . Напряжение U для замкнутой цепи (
. Напряжение U для замкнутой цепи ( ) равно э.д.с. ε, для незамкнутой – э.д.с. плюс разность потенциалов и просто разности потенциалов, если э.д.с. отсутствует.
) равно э.д.с. ε, для незамкнутой – э.д.с. плюс разность потенциалов и просто разности потенциалов, если э.д.с. отсутствует. ,
, пропорциональна напряженности электрического поля
пропорциональна напряженности электрического поля 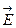 в проводнике (закон Ома в дифференциальной форме).
в проводнике (закон Ома в дифференциальной форме).


