Природа магнетизма. Ферромагнетики.

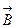Причина усиления в парамагнетиках состоит в том, что ато­мы или молекулы вещества представляют собой магнитные дипо­ли (обладают магнитными моментами). Эти диполи ориентируются во внешнем поле вдоль силовых линий и усиливают его. Если в соленоид вставлен сердечник из пара­магнетика, то дипольные моменты ато­мов (на рис. – стрелки) ориентируются вдоль по полю. В парамагнетике этот эффект очень слаб, и μ близко к единице, так как из-за теплового движения происходит только незначительная преимущественная ориентация диполей вдоль поля (рис.а). В молекулах диамагнетиков магнитный момент отсутствует, но он появляется при помещении диамагнетика во внешнее магнитное поле. Результирующий магнитный момент в диамагнетике мал, всегда направлен против внешнего поля и от температуры не зависит.

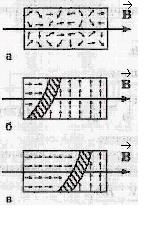Существуют вещества, в которых μ ~ 10² ÷10³ и более. Это железо, кобальт, никель, сплавы редких металлов (иттрия и др.). Такие вещества называются ферромагнетиками. В них очень ве­лико диполь-дипольное взаимодействие, в результате чего маг­нитные диполи атомов в отдельных областях выстраиваются параллельно друг другу без всякого внешнего поля. Этот эффект носит название спонтанного (самопроизвольного) намагничива­ния. На рис. б показаны две такие области, которые по­лучили название домены. Границы между доменами называются доменными стенками (заштриховано на рис. б и в).

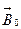Если приложить внешнее магнитное поле , например, вставив кусок ферромагнетика в соленоид, то домен с благоприятной ориентацией диполей разра­стается за счет домена с неблагоприятным намагничиванием. Это происходит путем поворота диполей в тонком слое доменной стен­ки, в результате чего стенка перемещается (рис. в). Ре­зультирующее поле будет намного больше, чем без ферромагнетика. Такая катушка с железным сердечни­ком, создающая сильное поле, называется электромагнитом.

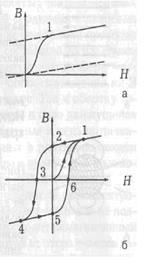В конце концов, весь объем тела превращается в один домен, наступает насыщение (точка 1 на рис. а и б). Если внешнее поле получается за счет тока во внешней катушке соленоида, то дальнейшее увеличение В будет происходить только за счет этого тока, т.е., за счет увеличения напряженности поля H. Таким образом, связь между Н и В оказы­вается нелинейной (рис. а), а μ ≠ const.

Если теперь уменьшать токв соле­ноиде, т.е., H, то В будет уменьшаться, но не до нуля, так как при H = 0 достаточно сильная остаточная индукция В_ОСТ (точка 2 на рис. б) получается за счет спон­танного намагничивания куска ферро­магнетика. Этот кусок можно вынуть из катушки, он будет более или менее долго намагниченным. Это постоян­ный магнит.

Если железный сердечник оста­вить в соленоиде, а ток соленоида пу­стить в обратную сторону, то остаточная индукция В_ОСТ исчезает при некотором отрицательном Н_К ( ко­эрцитивная сила, точка 3 на рис. б). Затем будет происходить намагни­чивание до насыщения в противопо­ложном направлении (точка 4). Если снова уменьшать H до нуля и затем увеличивать в положительном на­правлении, то мы пойдем не по пути 4 → 3→ 2 → 1, а по пути 4 → 5 (остаточное намагничивание в противоположном направлении) → 6 (положительная коэрцитивная сила Н_К) → 1. Так что зависимость B от Н не только нелинейная, но и неоднозначная. Это явление носит на­звание гистерезиса, а получающаяся петля (рис. б) назы­вается петлей гистерезиса.

В разных материалах форма петли гистерезиса разная. На рис. показаны петли гистерезиса для чистого же­леза (а) и для сплавов, из которых делают постоянные маг­ниты (б).

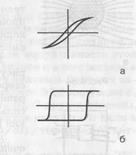При высоких температурах спонтанное намагничивание разрушается тепловым движением и ферромагнетик превращается в парамагнетик.

 

Энергия магнитного поля. Когда в катушке с индуктивностью L и сопротивлением течет изменяющийся ток I (t), к катушке подводится электрическая мощность:

.

Полная работа, необходимая для увеличения силы тока от нуля до I, равна:
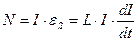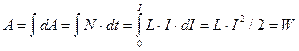. Эта работа равна энергии W, запасенной катуш­кой индуктивности, в которой течет ток.

Эту энергию можно рассматривать как энергию магнитного поля и выразить непосредственно через индукцию магнитного поля. Действительно, подставив вместо L для индуктивности соленоида L = μ₀ μ n² V (),

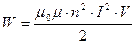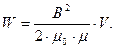и учитывая, что индукция магнитного поля внут­ри соленоида равна В = μ₀ μ· n·I, получим: Эта формула справедлива для однородного поля, заполняющего объем V. В самом общем случае энергия магнитного поля, локализованного в некотором объеме пространства, определяется как: 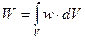, где 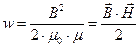– объемная плотность энергии (энергия в единице объема).