
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Кинематика вращательного движения.Содержание книги
Поиск на нашем сайте
Если точка вращается вокруг неподвижной оси, то она описывает окружность с центром на оси вращения, а плоскость этой окружности перпендикулярна оси вращения. Быстроту и направление вращения характеризуют угловой скоростью
Для характеристики неравномерного движения по окружности используется векторная величина, называемая угловым ускорением
Если движение материальной точки ускоренное, то векторы угловой скорости и углового ускорения совпадают по направлению; если движение замедленное, то эти векторы направлены в противоположные стороны. Такие векторы, направление которых совпадает с направлением некоторой оси, называются аксиальными. У них нет определенной точки приложения, они могут изображаться в любом месте на оси вращения. При равнопеременном вращении для величин угловой скорости и углового ускорения выполняются соотношения (аналогичные соотношениям для линейной скорости и линейного ускорения):
ОСНОВЫ ДИНАМИКИ. Законы динамики. В основе динамики лежат три закона Ньютона. Первый закон Ньютона (закон инерции) касается движения тел, не испытывающих внешних воздействий: всякое тело сохраняет состояние покоя или равномерного прямолинейного движения до тех пор, пока воздействие со стороны других тел не заставит его изменить это состояние. Системы отсчета, жестко связанные с такими (свободными) телами, называются инерциальными системами отсчета (ИСО). Для количественного описания воздействия тел друг на друга вводится понятие силы. Сила — векторная величина Сила Второй закон Ньютона утверждает, что быстрота изменения скорости движения тела (ускорение) пропорциональна приложенной силе и происходит по направлению той прямой, по которой эта сила действует: В механике масса – основная характеристика тела, показывающая его способность противостоять ускоряющим силам, т.е. масса характеризует инертность материального тела. Масса тела зависит от его размеров и природы вещества. В механике масса – величина скалярная, положительная, аддитивная и постоянная. В единицах СИ масса измеряется в килограммах (кг), а сила – в ньютонах (Н). Второму закону Ньютона можно придать другую форму, учитывая определение ускорения: Если ввести понятие импульса материальной точки Второй закон Ньютона является уравнением движения материальной точки. Решая его можно определить зависимость координат и скорости материальной точки от времени. При этом, помимо вида функции F(x,y,z,t), должны быть заданы начальные условия: положение и скорость частицы в начальный момент времени. Третий закон Ньютона указывает, что воздействие тел друг на друга носит характер взаимодействия: силы, с которыми действуют друг на друга взаимодействующие тела, равны по величине, противоположны по направлению и никогда не уравновешивают друг друга, так как приложены к разным телам:
|
||||
|
Последнее изменение этой страницы: 2016-08-15; просмотров: 788; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.145.152.168 (0.005 с.) |

 , равной первой производной от углового перемещения
, равной первой производной от углового перемещения  по времени:
по времени:  . Вектор угловой скорости
. Вектор угловой скорости 
 правого винта. Тогда векторы угловой
правого винта. Тогда векторы угловой 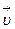 скоростей связаны соотношением:
скоростей связаны соотношением:  , где
, где  –радиус-вектор движущейся точки, а квадратные скобки означают векторное произведение. Модуль вектора линейной скорости υ=ω· rA, где rA – радиус окружности, по которой движется эта точка.
–радиус-вектор движущейся точки, а квадратные скобки означают векторное произведение. Модуль вектора линейной скорости υ=ω· rA, где rA – радиус окружности, по которой движется эта точка. иопределяемая соотношением:
иопределяемая соотношением: .
. .
.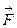 , которая определяется величиной или модулем F, направлениемв пространстве и точкой приложения. Если к материальной точке приложено несколько сил, их действие эквивалентно действию одной силы:
, которая определяется величиной или модулем F, направлениемв пространстве и точкой приложения. Если к материальной точке приложено несколько сил, их действие эквивалентно действию одной силы:  { принцип суперпозиции).
{ принцип суперпозиции).
 или
или  ;коэффициент пропорциональности т называется массой тела, а сила
;коэффициент пропорциональности т называется массой тела, а сила  или
или  .
. (это основная характеристика поступательного движения), товторой закон Ньютона принимает вид:
(это основная характеристика поступательного движения), товторой закон Ньютона принимает вид:  , т.е. быстрота изменения импульса тела равна силе, вызывающей это изменение.
, т.е. быстрота изменения импульса тела равна силе, вызывающей это изменение. .
.


