
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Круговые процессы (циклы). Цикл КарноСодержание книги
Поиск на нашем сайте Газ, получая тепло и расширяясь, производит работу. Для непрерывного получения работы нужно, чтобы рабочее тело все время возвращалось в исходное состояние и снова повторялся тот же процесс, т. е. чтобы процесс был круговым, циклическим. При этом какую-то работу надо совершать над газом, сжимая его и возвращая в исходное состояние. Для того, чтобы тепловая машина совершала положительную работу необходимо, чтобы расширение газа происходило при более высоком давлении, чем сжатие. Это возможно, если при расширении в систему будет поступать энергия Q1 извне, например, от нагревателя, а при сжатии энергия Q2 должна быть отдана внешней среде – холодильнику. После совершения цикла мы возвращаемся в исходное состояние с той же внутренней энергией. Следовательно, Δ U = 0, а подведенное тепло Q 1, за вычетом отдаваемого холодильнику Q 2, переходит в полезную работу A = Q1 – Q2. Для оценки эффективности работы вводят коэффициент полезного действия (кпд) тепловой машины: Работа машины тем эффективнее, чем больше можно получить от нее работы A и чем меньше надо подводить тепла от нагревателя Q1. Как показал С.Карно, максимальный кпд получается для цикла, состоящего из двух изотерм и двух адиабат (т.н. цикл Карно) (рис.) Газ расширяется из точки 1 в точку 2 по изотерме при температуре Т1. При этом в уравнении (19) Δ U = 0, работа расширения газа A > 0, т.е., к газу должна подводиться энергия от нагревателя Q1 > 0.
Пользуясь формулами (23), (36) и (38), можно получить для рассматриваемого цикла Карно: Из (39) следует, что кпд η тем больше, чем выше температура нагревателя Т1 и чем ниже температура холодильника Т2. Необратимые процессы
Другой пример: пусть газ находится и слева и справа от теплопроводной перегородки, но температура слева выше, чем температура справа (рис. б). Молекулы обмениваются с перегородкой кинетической энергией, и постепенно температуры обеих частей выравниваются. Такой процесс передачи тепла всегда необратим. Самопроизвольно средняя кинетическая энергия молекул (т. е. температура) слева сама не поднимется за счет кинетической энергии молекул справа. Любой процесс, сопровождающийся трением, также необратим, так как при этом энергия упорядоченного движения переходит в энергию беспорядочного движения молекул, т. е. в теплоту. Энтропия Пусть с рабочим веществом совершаются циклы, при каждом из которых подводится от нагревателя Q1, отдается холодильнику Q2 и производится работа А = Q1 – Q2. Из (38) и (39) можно получить:
Величина Qi /Ti называется приведенной теплотой. Обозначим ее Δ Si. Из (40) следует, что сумма приведенных теплот при циклическом процессе равна нулю. Это означает, что, какой бы циклический процесс мы ни совершали, если мы вернулись в исходное состояние, некоторая величина S не меняется ( Δ S = 0). Следовательно, S – функция состояния. Она получила название энтропии. Таким образом, состояние определяется не только внутренней энергией U, но и энтропией S. Если процесс не циклический и тело переходит из состояния 1 в другое состояние 2, то Рассмотрим теплопередачу при контакте двух тел при температурах Т1 и Т2 (Т1 > Т2) в теплоизолированной системе. Теплота Q, передаваемая телом 1, равна теплоте Q, полученной телом 2. Однако, тело 1 отдает ее при температуре Т1 и В тепловой машине часть теплоты, взятой от нагревателя, преобразуется в работу, а другая часть должна быть передана холодильнику. Нагреватель охлаждается, а холодильник нагревается. С одной стороны, мы знаем, что при этом энтропия возрастает. С другой стороны, к.п.д. такой тепловой машины будет постепенно падать, так как Энтропию можно связать со степенью упорядоченности системы. Увеличение энтропии соответствует увеличению беспорядка. Энтропия – это мера беспорядка. В наших примерах (рис.) система переходила из менее вероятного, упорядоченного, неравновесного состояния в более вероятное, неупорядоченное, равновесное. Вычислим изменение энтропии для идеального газа, исходя из дифференциальных выражений для изменения энтропии и I начала термодинамики: dS=δQ / T; Учитывая, согласно уравнению Клапейрона, что
Второе начало термодинамики Первое начало термодинамики (19, 41), т. е. закон сохранения энергии, справедливо при любом процессе обмена энергией. Оно не указывает направление процесса, для него неважно, будет ли тепло передаваться от горячего тела к холодному или наоборот, будет ли газ самопроизвольно расширяться или сжиматься и т. д.. Однако из рассмотренного выше вытекает, что: 1. Любая система, выведенная из состояния равновесия и предоставленная самой себе, возвращается в равновесное состояние. Таковы, например, необратимые процессы переноса: вещества (диффузия), энергии (теплопроводность), импульса упорядоченного движения (внутреннее трение или вязкость). 2. Механическая работа может быть полностью превращена в теплоту, т. е. энергия упорядоченного движения может полностью перейти в энергию неупорядоченного движения. Однако, энергия неупорядоченного движения (теплота) может быть преобразована в энергию упорядоченного движения (работу) лишь частично. Невозможен процесс, единственным результатом которого было бы полное превращение теплоты в работу. Т.е., кпд тепловой машины η < 1. 3. Предоставленная самой себе система всегда переходит из менее вероятного в более вероятное состояние. Больцман получил соотношение, связывающее изменение энтропии при необратимых процессах с термодинамическими вероятностями (числом способов реализации того или иного состояния) начального W 1 и конечного W 2 состояний: Δ S = k · ℓn (W 2/ W 1). Из этого соотношения вытекает, что процессы с уменьшением энтропии не невозможны, а настолько маловероятны, что практически никогда не реализуются.
Используя понятие энтропии, можно сформулировать еще одно равносильное утверждение: «В замкнутой, изолированной системе (системе с постоянной энергией) при любых процессах энтропия не может убывать, т.е. ΔS≥0». Все эти формулировки эквивалентны. Все они указывают направление процессов в изолированной или что то же самое в предоставленной самой себе системе. Это и есть второе начало термодинамики – важнейший закон природы. Не следует думать, что этот закон вообще запрещает передачу тепла от холодного тела к нагретому. Это возможно, но только в незамкнутой (открытой) системе. Например, это осуществляется в холодильнике. Можно также уменьшить энтропию системы, например поршнем сжать газ и снова собрать его в одной половине сосуда. Можно увеличить порядок в системе (т. е. уменьшить энтропию), но для этого необходимо вмешательство внешних сил.
ФИЗИКА. Часть 2.
|
||
|
Последнее изменение этой страницы: 2016-08-15; просмотров: 844; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.33 (0.01 с.) |

 (38).
(38). При расширении по адиабате из точки 2 в точку 3 обмен теплотой равен нулю и работа расширения А производится за счет изменения внутренней энергии Δ U (газ охлаждается). Далее, внешние силы сжимают газ по изотерме 3 → 4 при температуре Т2. Здесь опять Δ U = 0, и из (19) следует, что А < 0, Q2 < 0. Чтобы произвести изотермическое сжатие, надо отводить тепло, отдавать его более холодному телу – холодильнику. Далее внешние силы сжимают газ по адиабате 4 → 1, возвращая газ в первоначальное состояние.
При расширении по адиабате из точки 2 в точку 3 обмен теплотой равен нулю и работа расширения А производится за счет изменения внутренней энергии Δ U (газ охлаждается). Далее, внешние силы сжимают газ по изотерме 3 → 4 при температуре Т2. Здесь опять Δ U = 0, и из (19) следует, что А < 0, Q2 < 0. Чтобы произвести изотермическое сжатие, надо отводить тепло, отдавать его более холодному телу – холодильнику. Далее внешние силы сжимают газ по адиабате 4 → 1, возвращая газ в первоначальное состояние. (39).
(39). Рассмотрим процесс расширения газа. Пусть имеется сосуд с перегородкой (рис. а) в левой части которого есть газ, а в правой – нет. Уберем перегородку. Газ расширится и займет обе части. Если молекулы друг с другом не взаимодействуют (идеальный газ), то общая внутренняя энергия при таком процессе не изменится (UI =UII). Однако состояние II отличается от состояния I тем, что тело из состояния II самопроизвольно, без вмешательства извне не вернется в состояние I. Если молекул мало, например 2 или 3, то, двигаясь хаотически, случайно, они все могут в какой-то момент оказаться в левой части, но если молекул много, то это крайне маловероятно. Поэтому процесс расширения газа в пустоту называют необратимым.
Рассмотрим процесс расширения газа. Пусть имеется сосуд с перегородкой (рис. а) в левой части которого есть газ, а в правой – нет. Уберем перегородку. Газ расширится и займет обе части. Если молекулы друг с другом не взаимодействуют (идеальный газ), то общая внутренняя энергия при таком процессе не изменится (UI =UII). Однако состояние II отличается от состояния I тем, что тело из состояния II самопроизвольно, без вмешательства извне не вернется в состояние I. Если молекул мало, например 2 или 3, то, двигаясь хаотически, случайно, они все могут в какой-то момент оказаться в левой части, но если молекул много, то это крайне маловероятно. Поэтому процесс расширения газа в пустоту называют необратимым.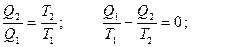 (40).
(40). . Когда тело получает теплоту (Q > 0), его энтропия возрастает, когда теряет (Q < 0) – энтропия уменьшается. При адиабатическом процессе (Q = 0) ΔS = 0 и S=const, поэтому адиабатический процесс называют еще изоэнтропийным.
. Когда тело получает теплоту (Q > 0), его энтропия возрастает, когда теряет (Q < 0) – энтропия уменьшается. При адиабатическом процессе (Q = 0) ΔS = 0 и S=const, поэтому адиабатический процесс называют еще изоэнтропийным. , а тело 2 получает ее при температуре Т2 и
, а тело 2 получает ее при температуре Т2 и  Так как Т1 > T2, следовательно, │Δ S 2│>│Δ S 1│, так что в целом при таком процессе энтропия возрастает. Т.о., при необратимых процессах энтропия увеличивается.
Так как Т1 > T2, следовательно, │Δ S 2│>│Δ S 1│, так что в целом при таком процессе энтропия возрастает. Т.о., при необратимых процессах энтропия увеличивается. и при Т1 → T2 к.п.д. η → 0. Общая энергия системы, включающей нагреватель, холодильник, рабочее вещество и тело, над которым производится работа, остается неизменной, но работы получается все меньше и меньше. В пределе, когда Т1 = T2, теплота от нагревателя не может быть использована вовсе. Тогда внутренняя энергия нагревателя становится бесполезной. Таким образом, возрастание энтропии соответствует обесцениванию энергии.
и при Т1 → T2 к.п.д. η → 0. Общая энергия системы, включающей нагреватель, холодильник, рабочее вещество и тело, над которым производится работа, остается неизменной, но работы получается все меньше и меньше. В пределе, когда Т1 = T2, теплота от нагревателя не может быть использована вовсе. Тогда внутренняя энергия нагревателя становится бесполезной. Таким образом, возрастание энтропии соответствует обесцениванию энергии. (41)
(41) , и подставив p в δ Q, а δ Q в выражение для d S, получим:
, и подставив p в δ Q, а δ Q в выражение для d S, получим: , которое после интегрирования определяет изменение энтропии идеального газа при переходе от состояния 1 с Т 1 и V 1 к состоянию 2 с Т 2 и V 2:
, которое после интегрирования определяет изменение энтропии идеального газа при переходе от состояния 1 с Т 1 и V 1 к состоянию 2 с Т 2 и V 2:  (42).
(42).


