
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Теплоемкость. Молярная теплоемкость газа. Степени свободы.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте Под теплоемкостью С телапонимают то количество тепла, которое надо сообщить телу, чтобы повысить его температуру на один градус Кельвина:
Если передается энергия не всему телу, а одному килограмму, то говорят об удельной теплоемкости с = С/m (Дж/(кг·К)). Если речь идет об одном моле, то говорят о молярной теплоемкости Поскольку при переходе тела из одного состояния в другое δQ зависит от процесса, по которому производится этот переход, теплоемкость тоже зависит от процесса. Если процесс изохорический (V = const), то теплоемкость обозначается СV. Если процесс изобарический, то – Ср. При изотермическом процессе dT = 0, a δQ не равно нулю и соответствующая теплоемкость устремляется к бесконечности СТ → ∞. Определим СV (теплоемкость 1 моля при постоянном объеме), использовав первое начало термодинамики в дифференциальной форме (19). Поскольку V = const, то dV = 0 и δA = 0 и для СV получаем:
Значок вне скобок указывает на тип процесса, т. е. что V = const. Соотношение (25) означает, что при постоянном объеме все подводимое тепло идет только на изменение внутренней энергии U. При изобарическом процессе (р = const), для теплоемкости Ср получаем:
Найдем (dV/dT)p из уравнения Клапейрона (4):
и подставив в (26), получим уравнение Майера: Cp больше, чем СV, так как подведенная теплота идет не только на увеличение внутренней энергии, но и на работу расширения газа. Определим dU/dT, так как эта производная входит в (25) и (26). Для идеального газа внутренняя энергия равна сумме средних кинетических энергий всех N молекул:
Вращение вокруг оси z не дает вклада в энергию, так как энергия вращательного движения равна J·ω2/2 = m·r2·ω2/2, а двухатомная молекула не имеет пространственной протяженности вдоль осей x и y. Надо не только задать три координаты, чтобы определить положение центра масс молекулы в пространстве, но и задать еще две (вращательные) координаты, чтобы определить ее ориентацию в пространстве. Т.о., число степеней свободы для двухатомной молекулы i = 5. Для трех- и более атомной молекулы вклад в энергию даст и вращение вокруг оси z. Для них i = 6. Молекулы мы считали жесткими; колебательные степени свободы не Итак, для жестких молекул внутренняя энергия и молярные теплоемкости равны: Все это сильно упрощенные рассуждения, непригодные, например, при очень низких или высоких температурах. Более последовательная теория теплоемкости строится на основе квантовой физики. Адиабатический процесс Процесс без обмена теплотой с окружающей средой называется адиабатическим. Он может происходить, если газ (или другое тело) окружен абсолютно не проводящей тепло оболочкой или процесс происходит очень быстро, так что газ не успевает обменяться теплом с другими телами. При таких процессах первое начало термодинамики упрощается: δQ = 0; dU = – δА. (32). Это означает, что если над газом производить работу ( δ А < 0), то dU > 0. Внутренняя энергия газа возрастает, он нагревается. Если же газ расширяется, то он сам производит работу δ А > 0 за счет собственной внутренней энергии и dU < 0. В результате он охлаждается. Согласно (25): dU =ν · CV · dT. Дляδ А используем соотношение (20). Тогда выражение (32) для адиабатического процесса можно записать так:
Подставим сюда р из уравнения Клапейрона-Менделеева (4) иполучим:
Проинтегрируем последнее выражение для пределов изменения переменных от T 1 до T 2 и от V 1 до V 2 и введя обозначение а используя Т = p·V/(ν·R), получаем Соотношения (36-37) носят название уравнений Пуассона или адиабаты. γ – показатель адиабаты.
При любых других процессах (неизотермических и неадиабатических) всегда можно связь между р и V написать в виде (37), но γ уже не будет равна Ср/СV. В этих случаях процесс называется политропическим, а γ – показателем политропы. Можно сказать, что для изотермического (T =const) процесса γ = 1, для изобарического (р = const) γ = 0, для изохорического (V = const) γ = ∞. На рисунке б показаны различные процессы расширения газа: 1 – изотерма, 2 – адиабата, 3 – изохора, 4 – изобара, 5 – политропа. Процессы 2, 3 идут с охлаждением, а 4, 5 – с нагреванием газа.
|
||
|
Последнее изменение этой страницы: 2016-08-15; просмотров: 1049; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.33 (0.008 с.) |

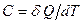 (Дж/К) (24)
(Дж/К) (24)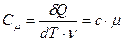 , измеряемой в Дж/(моль·К). О ней мы и будем говорить далее.
, измеряемой в Дж/(моль·К). О ней мы и будем говорить далее. (25).
(25). (26).
(26). (27)
(27) (28).
(28).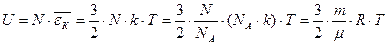 (29).Тогда
(29).Тогда  ;
;  ;
;  (30). В выражении для
(30). В выражении для  учитывалась только кинетическая энергия поступательного движения в трехмерном пространстве. Число независимых координат, необходимых, чтобы полностью определить положение тела в пространстве, называется числом степеней свободы i. Будем считать атомы, из которых состоит молекула, материальными точками, тогда одноатомная молекула имеет три степени свободы поступательного движения i = 3. И т.о., на каждую степень свободы приходится энергия по (1/2) kТ.
учитывалась только кинетическая энергия поступательного движения в трехмерном пространстве. Число независимых координат, необходимых, чтобы полностью определить положение тела в пространстве, называется числом степеней свободы i. Будем считать атомы, из которых состоит молекула, материальными точками, тогда одноатомная молекула имеет три степени свободы поступательного движения i = 3. И т.о., на каждую степень свободы приходится энергия по (1/2) kТ.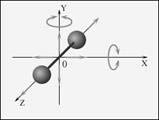 Если молекула двухатомная (рис.), то, кроме поступательного движения, она может еще вращаться вокруг осей x и y.
Если молекула двухатомная (рис.), то, кроме поступательного движения, она может еще вращаться вокруг осей x и y.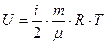 ;
;  (31).
(31).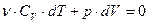 (33).
(33). ;
;  (34).
(34). (35). получим:
(35). получим: 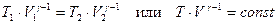 (36),
(36),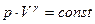 (37).
(37). Поскольку γ > 1, давление в (37) обратно пропорционально не V, как было при изотермическом процессе, а Vγ, т. е. давление убывает с увеличением объема быстрее. На рисунке a кривые 1 и 2 – изотермы (Т 2 < T 1), а кривая 3 – адиабата.
Поскольку γ > 1, давление в (37) обратно пропорционально не V, как было при изотермическом процессе, а Vγ, т. е. давление убывает с увеличением объема быстрее. На рисунке a кривые 1 и 2 – изотермы (Т 2 < T 1), а кривая 3 – адиабата.


