Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Определение отношения удельных теплоемкостей газов методом клемана-дезормаСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Приборы и принадлежности: стеклянный баллон с трехходовым краном, манометр, воздушный насос. Краткая теория Опыт показывает, что количество теплоты
где с - удельная теплоемкость вещества. Из формулы (1) следует
Отсюда видно, что удельной теплоемкостью называется количество теплоты, необходимое для нагревания вещества массой 1 кг на 1 К. Положив m=1 кг, Кроме удельной теплоемкости вещества вводится понятие молярной теплоемкости С. Молярной теплоемкостью называется количество теплоты, необходимое для нагревания моля вещества на 1 К. Из определения удельной теплоемкости следует, что она связана с молярной соотношением
где μ - молярная масса вещества. Единицей С является Дж/(моль×К). Состояние газа может быть охарактеризовано тремя величинами - параметрами состояния: давлением p, объемом V и температурой T. Уравнение, связывающее эти величины, называется уравнением состояния вещества. Для случая идеального газа уравнением состояния является уравнение Менделеева-Клапейрона, которое для одного моля газа будет иметь вид pV = RT (4) где R - универсальная газовая постоянная. Величина теплоемкости газов зависит от условий нагревания. Выясним эту зависимость, воспользовавшись уравнением состояния (4) и первым началом термодинамики, которое можно сформулировать следующим образом: количество теплоты По определению теплоемкости Из уравнения (6) видно, что теплоемкость может иметь различные значения в зависимости от способов нагревания газа, так как одному и тому же значению Внутренняя энергия 1 моля газа где i- число степеней свободы. Числом степеней свободы газа называется число независимых координат, определяющих положение тела в пространстве. При движении точки по прямой линии для оценки ее положения надо знать одну координату, т.е. точка имеет одну степень свободы. Если точка движется по плоскости, ее положение характеризуется двумя координатами, т.е. точка обладает двумя степенями свободы. Положение материальной точки в пространстве определяется тремя координатами.
Рассмотрим основные процессы, протекающие в идеальном газе при изменении температуры, когда масса газа остается неизменной и равна одному молю. Количество теплоты, необходимое для нагревания одного моля газа на 1К, определяется молярной теплоемкостью. Изохорический процесс. Процесс называется изохорическим, если объем тела при изменении температуры остается постоянным, т.е. V=const. В этом случае: Изобарический процесс. Процесс, протекающий при постоянном давлении (P =const), называется изобарическим. Для этого случая формула (6) перепишется в виде: Из уравнения газового состояния (4) получаем:
Но Р =const и d Р =0. Следовательно, Сравнив (8) и (11), получим Изотермический процесс. Изотермическим процессом называется процесс, протекающий при постоянной температуре (T=const). В этом случае Адиабатический процесс. Процесс, протекающий без теплообмена с окружающей средой, называется адиабатическим. Первое начало термодинамики для такого процесса будет иметь вид т.е. при адиабатическом процессе расширения или сжатия, работа совершается газом только за счет изменения запаса внутренней энергии. Выведем уравнение адиабатического процесса. При адиабатическом расширении работа совершается за счет убыли внутренней энергии
Но Разделив уравнение (10) на (12) и учитывая (12), получим
где Интегрируя и потенцируя, получим уравнение Пуассона:
Используя формулы (11) и (12), для γ можно получить:
Эта формула справедлива как для молярных, так и для удельных теплоемкостей газов. Таким образом, по значениям теплоемкостей все газы можно разделить на три сорта: одноатомные, двухатомные, многоатомные газы. Описание и теория метода Предлагаемый метод определения g основан на применении уравнений адиабатического и изохорического процессов.
Обозначим через Т1 термодинамическую температуру окружающего воздуха и через р1 - давление газа внутри сосуда, соответствующее показанию манометра h1. Очевидно, давление, установившееся в баллоне, будет равно где р0 - атмосферное давление (конечно, при этом р0 и h1 должны быть выражены в одинаковых единицах). Эти два параметра Т1 и р1 характеризуют состояние газа, которое мы назовем первым состоянием газа. Если теперь быстро открыть кран, то воздух в баллоне будет расширяться адиабатически, пока давление его не сделается равным р0; при этом он охладится до температуры Т2. Это будет второе состояние газа: Т2 и р0. Если сразу после открывания снова закрыть кран, то давление внутри баллона начнет возрастать вследствие того, что охладившийся при расширении воздух в баллоне станет снова нагреваться. Возрастание давления прекратится, когда температура воздуха в баллоне сравняется с внешней температурой Т1. Обозначим давление воздуха в баллоне в этот момент через р2 и соответствующее показание манометра - через h2. Это будет третье состояние газа: Т1 и р2. Ясно, что К переходу из первого состояния во второе (процесс адиабатического расширения) применяем уравнение Пуассона в форме: Эта форма уравнения Пуассона может быть легко получена из обычной (13) Подставляя в уравнение (18) значение р1 из (15) и переставляя члены, получаем:
Разлагая оба двучлена по биному Ньютона и ограничиваясь членами первого порядка малости, получаем:
Но выражение, стоящее в левой части этого уравнения, есть не что иное, как h2; действительно, подставив в уравнение (17) значение р1 из уравнения (16) и разрешив его относительно h2, получим: Следовательно, можно записать: Выполнение работы С помощью трехходового крана Д баллон может соединяться с воздушным насосом, с атмосферой либо перекрываться совсем. Для проведения измерений кран ставят в положение, при котором воздух нагнетается в баллон с помощью насоса. Когда разность уровней в манометре достигает 20-25 делений шкалы манометра, отключают баллон от насоса и атмосферы. После того как давление окончательно установится, производят отсчет h1 - разности уровней жидкости в обоих коленах манометра (если нуль шкалы манометра находится внизу, то h1 определяется как разность уровней в манометре; если нуль шкалы находится в середине, то берется сумма показаний манометра по обе стороны от нуля). Затем производят на некоторый момент сообщение баллона с атмосферой и быстро его перекрывают (рекомендуется перекрывать баллон сразу после прекращения звука выходящего воздуха). Когда давление окончательно установится, производят второй отсчет по манометру - h2. Опыт повторить не менее десяти раз, меняя всякий раз величину h1. Подставляя в формулу (19) значения h1 и h2, взятые из отдельных наблюдений, находят величину g, а все результаты заносят в таблицу:
Окончательно величину g находят как среднее значение всех g, полученных при наблюдении. Контрольные вопросы 1. Что называется удельной (молярной) теплоемкостью вещества? 2. Почему теплоемкости газа зависят от условий его нагревания? 3. Что называется числом степеней свободы тела? 4. Чему равно отношение молярной теплоемкости газа и его удельной теплоемкости? 5. Чему равно g для воздуха? 6. Дайте определение адиабатического процесса и покажите, как в координатах P и V графически изображаются адиабатический и изотермический процессы. РАБОТА № 13 ОПРЕДЕЛЕНИЕ СКОРОСТИ ЗВУКА В ВОЗДУХЕ И ОТНОШЕНИЕ УДЕЛЬНЫХ ТЕПЛОЕМКОСТЕЙ СР/СV ДЛЯ ВОЗДУХА МЕТОДОМ СТОЯЧИХ ЗВУКОВЫХ ВОЛН Особым примером результата интерференции двух волн служат так называемые стоячие волны, образующиеся в результате наложения двух встречных когерентных волн с одинаковыми амплитудами. Предположим, что две плоские волны с одинаковыми амплитудами, отстоящие на полпериода, распространяются - одна вдоль положительного направления Y, другая - вдоль отрицательного направления Y (рис. 1). Если начало координат в такой точке, в которой встречные волны имеют одинаковые фазы, и выбрать отсчет времени так, чтобы начальные фазы оказались равными нулю, то уравнения обеих бегущих волн будут иметь вид: : Разные знаки в аргументах синусов обусловлены тем, что волны движутся навстречу друг другу, т.е. их скорости V различаются по знаку. По принципу суперпозиции (наложения) интерферирующих волн смещение X в результирующей волне будет равно:
Пользуясь выражением для суммы синусов получаем
Каждая точка совершает гармоническое колебание с периодом Т. В данном уравнении стоячей волны (4) амплитуда Аст для каждой точки волны вполне определена, но при переходе от одной точки волны к другой она изменяется в зависимости от расстояния Y. На рисунке 1 видно, что ряд точек на оси ОY в результате интерференции встречных волн вообще не колеблется. А именно, это все те точки, для которых где n=..,-2,-1,0,1,2,.. Точки на оси ОY, координаты которых задаются условием (5), называются узлами (т. 2, 4, 6 и т.д.). Если же Из (5) и (6) нетрудно найти, что расстояние между двумя соседними узлами (или пучностями), называемое длиной стоячей волны, будет равно Как известно, длиной бегущей волны называется расстояние, на которое распространяются колебания за один период, т.е. l=vT. Так как T=1/n, где n - частота колебаний, то V=ln. Тогда, используя (7), получим, что скорость распространения для бегущей волны равна: V=2lcnn (8) В отличие от бегущих волн в стоячей волне отсутствует перенос энергии вследствие того, что образующие эту волну прямая и обратная бегущие волны переносят энергию в равных количествах и в противоположенных направлениях. Скорость распространения звуковых волн во многом зависит от упругих свойств среды, в которой они распространяются. При распространении звуковой волны частицы среды совершают колебания около положения равновесия. При этом происходит передача энергии без переноса вещества. Если колебания частиц среды происходят в том же направлении, что и распространение энергии, волны называются продольными. Если колебания частиц перпендикулярны к направлению распространения энергии, то такие волны называются поперечными. Можно показать, что скорость распространения продольных звуковых волн в сплошной среде определяется формулой где Е - модуль упругости среды (модуль Юнга), а r - плотность среды. Кроме того, по закону Гука для деформируемого упругого стержня:
где s - механическое напряжение, т.е. сила, отнесенная к единице поперечного сечения стержня и измеряемая в тех же единицах, что и давление; ∆l ⁄ l - относительное изменение длины стержня. Поскольку основной средой, в которой распространяются звуковые волны, является воздух, рассмотрим вопрос о скорости распространения упругих продольных волн в газах. Для столба газа величина s в (10) должна быть заменена добавочным давлением ∆p, вызывающим сжатие газа. Относительную линейную деформацию ∆l ⁄ l можно заменить относительной объемной деформацией ∆V ⁄ V, так как мы полагаем, что столб газа сжимается лишь вдоль своей длины, не меняя своего поперечного сечения. Таким образом, имеем
Полагая изменение давления и объема бесконечно малыми, можно записать (11) в виде: Знак минус ставим потому, что положительному dp, т.е. увеличению давления, соответствует уменьшение объема, т.е. отрицательное dV, тогда
Звуковые колебания происходят настолько быстро, что сжатие и разряжение газа будут происходить без теплообмена, т.е. адиабатически. Для такого газового процесса справедливо уравнение Пуассона: PVg=const (14), где g=Cp/Cv - отношение удельных (молярных) теплоемкостей газа. Дифференцируя уравнение (14) сначала по р, а затем по V, получаем следующее соотношение: Подставляя (15) в (13), находим, что Из уравнения Клапейрона-Менделеева для любой массы газа: где m - молярная масса газа, можно найти плотность газа r: Подставляя уравнения (16) и (17) в формулу (9), получим выражение для скорости звука в газе Таким образом, для данного газа скорость звука прямо пропорциональна корню квадратному из термодинамической температуры T и не зависит от давления газа Р. Зная скорость звука в данной газовой среде и его термодинамическую температуру, из (18) можно определить величину g=СР / CV: Описание установки В данной работе для определения скорости звука при комнатной температуре, а затем g=СР / CV используется установка, изображенная на рисунке 2. Здесь Д - длинная стеклянная трубка с миллиметровой шкалой. Нижним концом трубка соединяется резиновым шлангом с сосудом S, заполненным жидкостью. На верхний конец трубки надето эбонитовое кольцо. К верхнему отверстию которого прикреплен электроакустический преобразователь от телефона. В боковую стенку нижней части эбонитового кольца вставлена слуховая трубка С. Катушка телефонного преобразователя подключается к выходным клеммам звукового генератора (ЗГ). Через катушку протекает синусоидальный ток, генерируемый звуковым генератором. Колебания мембраны телефона будут передаваться частицам воздуха, заключенным в трубке Д, в результате чего в ней образуются воздушные звуковые волны. При отражении от жидкости прямая и отраженная волны накладываются друг на друга и образуют стоячую звуковую волну. Перемещая уровень жидкости в трубке Д подниманием или опусканием сосуда S, добиваются резонанса, т.е. максимального звучания воздушного столба, заключенного в трубке. Длину звуковой волны можно вычислить, измерив расстояние l, на которое должен переместиться уровень жидкости в трубке Д при переходе от одной точки с максимальным звучанием к следующей. (Очевидно, что l =lСТ.) Выполнение работы Включают звуковой генератор и по указанию преподавателя устанавливают его на частоту в пределах от 800 до 1500 Гц.
Подобным образом находят последующие за этим другие максимумы звучания при нескольких подъемах и опусканиях уровня. После усреднения отсчетов положения максимумов звучания находят разность между средними соседними максимумами звучания По формуле (8) вычисляют среднее значение скорости звука при данной температуре и для данной частоты. Таблица 1
Аналогичные измерения проводят для других частот и все данные заносят в таблицы. По формуле (9), используя полученные значения скорости звука, получают ряд значений γ и усредняют их. Контрольные вопросы 1. Как связаны скорость распространения колебаний с упругостью среды? 2. Почему можно применять уравнения адиабатического процесса к газу, в котором распространяется звуковая волна? 3. Объясните возникновение стоячих волн. 4. Переносит ли стоячая волна энергию? 5. Что называется теплоемкостью? 6. Почему теплоемкость газа при постоянном объеме СV не равна теплоемкости газа при постоянном давлении СР? РАБОТА №14
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-08-16; просмотров: 913; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.227.72.27 (0.011 с.) |

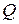 , необходимое для нагревания массы однородного вещества от температуры Т1 до Т2 градусов, пропорционально массе вещества и изменению температуры:
, необходимое для нагревания массы однородного вещества от температуры Т1 до Т2 градусов, пропорционально массе вещества и изменению температуры: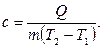 (2)
(2)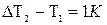 , получим единицу удельной теплоемкости:
, получим единицу удельной теплоемкости: 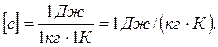
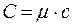 , (3)
, (3)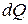 , переданное системе, затрачивается на увеличение ее внутренней энергии
, переданное системе, затрачивается на увеличение ее внутренней энергии 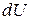 и на работу
и на работу 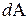 , совершаемую системой против внешних сил
, совершаемую системой против внешних сил 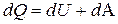 . (5)
. (5)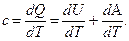 (6)
(6)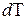 могут соответствовать различные значения
могут соответствовать различные значения 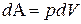 .
.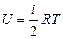 , (7),
, (7), Число степеней свободы молекулы обычно обозначается буквой i-. Молекулы, которые состоят из одного атома, считаются материальными точками и имеют число степеней свободы i- =3. Такими являются молекулы аргона, гелия и др. Двухатомные молекулы (H2, N2 и др.) обладают числом степеней свободы i =5; они имеют три степени свободы поступательного движения вдоль осей X, Y, Z и две степени свободы вращения вокруг осей X и Z (рис.1, а). Вращением вокруг оси Y можно пренебречь, т.к. момент инерции ее относительно этой оси очень мал. Молекулы, состоящие из трех и более жестко связанных атомов, не лежащих на одной прямой (рис.1, б), имеют число степеней свободы i = 6: три степени свободы поступательного движения и три степени свободы вращения вокруг осей X, Y, Z. Столько же степеней свободы имеют и другие многоатомные молекулы.
Число степеней свободы молекулы обычно обозначается буквой i-. Молекулы, которые состоят из одного атома, считаются материальными точками и имеют число степеней свободы i- =3. Такими являются молекулы аргона, гелия и др. Двухатомные молекулы (H2, N2 и др.) обладают числом степеней свободы i =5; они имеют три степени свободы поступательного движения вдоль осей X, Y, Z и две степени свободы вращения вокруг осей X и Z (рис.1, а). Вращением вокруг оси Y можно пренебречь, т.к. момент инерции ее относительно этой оси очень мал. Молекулы, состоящие из трех и более жестко связанных атомов, не лежащих на одной прямой (рис.1, б), имеют число степеней свободы i = 6: три степени свободы поступательного движения и три степени свободы вращения вокруг осей X, Y, Z. Столько же степеней свободы имеют и другие многоатомные молекулы.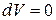 . Следовательно, и
. Следовательно, и 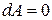 , т.е. при этом вся подводимая к газу теплота идет на увеличение его внутренней энергии. Тогда из уравнения (6) следует, что молярная теплоемкость газа при постоянном объеме равна
, т.е. при этом вся подводимая к газу теплота идет на увеличение его внутренней энергии. Тогда из уравнения (6) следует, что молярная теплоемкость газа при постоянном объеме равна 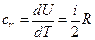 . (8)
. (8)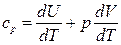 . (9)
. (9)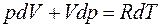 . (10)
. (10)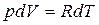 . Подставляя это выражение в уравнение (9), получим
. Подставляя это выражение в уравнение (9), получим 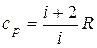 . (11)
. (11)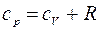 . (12)
. (12)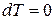 и
и 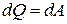 , т.е. внутренняя энергия газа остается постоянной и все подводимое тепло расходуется на работу.
, т.е. внутренняя энергия газа остается постоянной и все подводимое тепло расходуется на работу.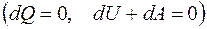 :
: 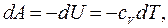
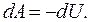
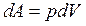 и
и 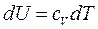 , значит,
, значит, 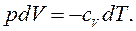
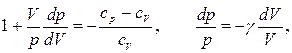
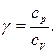 называется отношением удельных теплоемкостей
называется отношением удельных теплоемкостей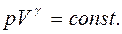 (13)
(13)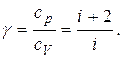 (14)
(14)
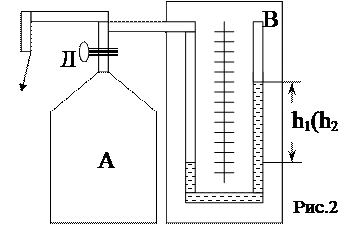 Установка состоит из стеклянного баллона А, соединенного с манометром В и насосом (рис.2). Посредством крана Д баллон может быть соединен с атмосферой, и будем считать, что первоначально в нем было атмосферное давление. Если с помощью насоса накачать в баллон некоторое количество воздуха и закрыть кран, то давление в баллоне повысится; но если это повышение было произведено достаточно быстро, то манометрический столбик не сразу займет окончательное положение, так как сжатие воздуха было адиабатическим и, следовательно, температура его повысится. Окончательная разность уровней в манометре h установится только тогда, когда температура воздуха внутри баллона сравняется, благодаря теплопроводности стенок, с температурой окружающего воздуха.
Установка состоит из стеклянного баллона А, соединенного с манометром В и насосом (рис.2). Посредством крана Д баллон может быть соединен с атмосферой, и будем считать, что первоначально в нем было атмосферное давление. Если с помощью насоса накачать в баллон некоторое количество воздуха и закрыть кран, то давление в баллоне повысится; но если это повышение было произведено достаточно быстро, то манометрический столбик не сразу займет окончательное положение, так как сжатие воздуха было адиабатическим и, следовательно, температура его повысится. Окончательная разность уровней в манометре h установится только тогда, когда температура воздуха внутри баллона сравняется, благодаря теплопроводности стенок, с температурой окружающего воздуха.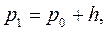 (15)
(15)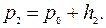
 (16) Так как переход от второго состояния (после закрытия крана) к третьему произошел без изменения объема, то можно применить здесь закон Гей-Люссака:
(16) Так как переход от второго состояния (после закрытия крана) к третьему произошел без изменения объема, то можно применить здесь закон Гей-Люссака: 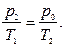 (17)
(17)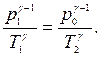 (18)
(18)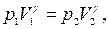 если воспользоваться для этой цели уравнением состояния газа
если воспользоваться для этой цели уравнением состояния газа 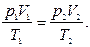 Возводя последнее уравнение в степень g и разделив его почленно на уравнение Пуассона, получим:
Возводя последнее уравнение в степень g и разделив его почленно на уравнение Пуассона, получим: 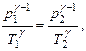 т.е. уравнение, аналогичное (18).
т.е. уравнение, аналогичное (18).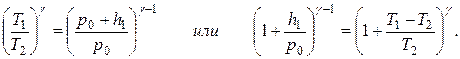
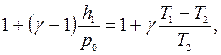 откуда
откуда 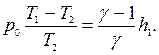
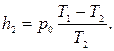
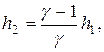 откуда окончательно находим:
откуда окончательно находим: 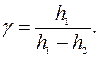 (19)
(19)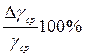
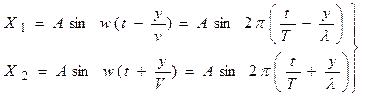 (1)
(1)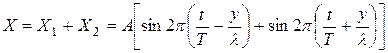
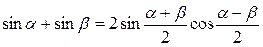 ,
,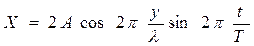 . (2)
. (2)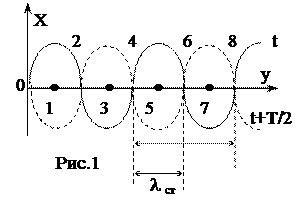 Это есть уравнение стоячей волны, которое определяет смещение любой точки среды. В этом уравнении множитель
Это есть уравнение стоячей волны, которое определяет смещение любой точки среды. В этом уравнении множитель 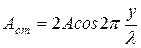 (3) не зависит от времени и определяет амплитуду любой колеблющейся точки с координатой x. Поэтому уравнение стоячей волны (2) можно записать так:
(3) не зависит от времени и определяет амплитуду любой колеблющейся точки с координатой x. Поэтому уравнение стоячей волны (2) можно записать так: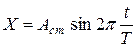 (4)
(4)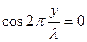 . Т.е.
. Т.е. 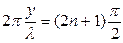 , или
, или 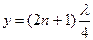 , (5)
, (5)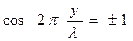 , то амплитуда колебаний максимальна; такие точки называются n пучностями (т. 2, 3, 5, и т.д.). Для них
, то амплитуда колебаний максимальна; такие точки называются n пучностями (т. 2, 3, 5, и т.д.). Для них 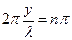 (6)
(6)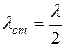 (7), где l - длина бегущих волн.
(7), где l - длина бегущих волн.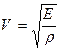 , (9)
, (9)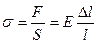 , (10)
, (10)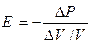 (11)
(11)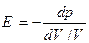 (12)
(12)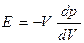 (13)
(13)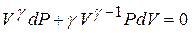 (15)
(15)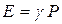 (16)
(16)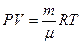 ,
,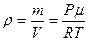 (17)
(17)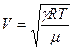 (18)
(18)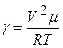 (19)
(19)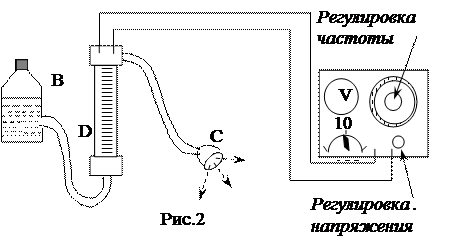 Перемещая уровень жидкости в трубке поочередно вверх и вниз, определяют по слуху максимум звучания воздушного столба. Отмечают его положение по миллиметровой шкале.
Перемещая уровень жидкости в трубке поочередно вверх и вниз, определяют по слуху максимум звучания воздушного столба. Отмечают его положение по миллиметровой шкале.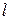 и так же усредняют их.
и так же усредняют их. , мм
, мм
 мм
мм
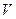 ,
м/с
,
м/с
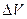 ,
м/с
,
м/с
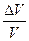 100%
100%