
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
При помощи крутильных колебанийСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Приборы и принадлежности: крутильный маятник, набор тел. Описание установки Общий вид крутильного маятника показан на рис. 1.Крутильный
Конструкция рамки позволяет закреплять исследуемые тела 10, значительно отличающиеся друг от друга по внешним размерам. Тела крепятся при помощи подвижной балки 12, которая перемещается по направляющим между неподвижными балками. Подвижная балка закрепляется путем затягивания гаек на зажимных втулках. Описание метода определения моментов инерции твердых тел. При отклонении рамки от положения равновесия возникает момент сил упругости (кручения) проволоки, пропорциональной по закону Гука углу закручивания a и направленный в противоположную сторону: M=- k a, (1) где k – коэффициент упругости проволоки. Тормозящим моментом сил трения, который будет в нашем случае мал по сравнению с моментом упругости можно пренебречь. Таким образом, основной закон динамики для возникших крутильных колебаний M=Jb с учетом формулы углового ускорения
где - угловое ускорение, а J – момент инерции рамки. Уравнение (2) представляет собой дифференциальное уравнение гармонических колебаний. Решение его, как известно, является функция
где a0 – амплитуда, w - собственная циклическая частота, j - начальная фаза колебаний.Частота w может быть найдена подстановкой решения (3) в уравнение (2):: Тогда период колебаний Т будет равен: Таким образом, нахождение моментов инерции тел можно свести к определению периода крутильных колебаний при известном коэффициенте упругости проволоки k. Обозначим через Jk момент инерции исследуемого тела. Если коэффициент упругости k неизвестен, то найти Jk, определив период колебаний Т эт, некоторого эталонного тела, имеющего известный момент инерции J эт. В качестве эталонного тела можно взять любое тело, имеющее правильные геометрические размеры, момент инерции которого легко рассчитывается по известным формулам. (см. рис 5, стр. 6). Итак, обозначим через J 0 момент инерции ненагруженной рамки. Тогда период ее колебаний будет равен а период колебаний рамки с эталонным телом Очевидно, что период колебания рамки с исследуемым телом
Исключая из (6-8) коэффициент k, получим формулу для определения момента инерции исследуемого тела:
Выполнение работы 1. Подключить прибор к сети. По очереди нажать кнопки «сеть» и «сброс». На цифровом табло должны высвечиваться нули. 2. Отклонить рамку прибора таким образом, чтобы стрелка 9 приблизилась к сердечнику электромагнита 7, который зафиксирует рамку в заданном положении. Положение электромагнита задается преподавателем. 3. Нажать кнопку «пуск». При этом освобожденная рамка начнет совершать крутильные колебания. На цифровом табло будет высвечиваться число полных колебаний n и соответствующее им время колебаний. После завершения 10-20 колебаний нажать кнопку «стоп». Записать соответствующие показания n и t. По формуле T0 = t/n определить период колебаний ненагруженной рамки. Измерения проделать не менее трех раз и найти среднее значение T0. 4. Поместить эталонное тело между неподвижной и подвижной балками рамки. Затягивая гайки 12 на зажимных втулках, проверить надежность крепления эталонного тела. В нашей работе в качестве эталонных тел используются сплошные металлические цилиндры, момент инерции которых относительно оси цилиндра равен Тогда окончательная расчетная формула для определения момента инерции будет иметь следующий вид: 5. Повторяя последовательно пункты 1, 2, 3, определить период колебаний Т эт рамки с эталонным телом. 6. Заменить в рамке эталонное тело на тело с неизвестным моментом инерции (по указанию преподавателя) и в соответствии с п. 5 определить период колебаний Тх рамки с телом, момент инерции которого необходимо определить. 7. По формуле (10) определить неизвестный момент инерции, подставив в нее значения Т 0, Т эт, Тх и рассчитанное значение Jэт. 8. Определить моменты инерции того же тела относительно других осей вращения, для чего поменять положение тела в рамке и повторить пункты 6 и 7. 9. Для одного из полученных неизвестных моментов инерции необходимо оценить абсолютную и относительную погрешности измерений Контрольные вопросы 1. Что называется моментом инерции тела относительно оси вращения? В каких единицах измеряется момент инерции? 2. Может ли твердое тело иметь несколько моментов инерции? 3. Как связаны между собой момент силы и момент инерции тела? 4. Каким образом объясняется вращение фигуристов в пируэте? РАБОТА № 5-2
|
||||
|
Последнее изменение этой страницы: 2016-08-16; просмотров: 506; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.135.241.191 (0.008 с.) |

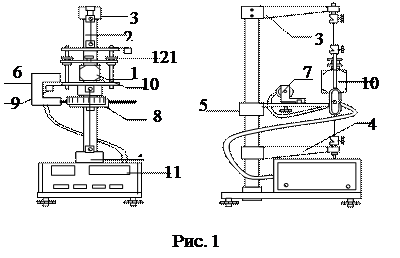 маятник состоит из рамки 1, подвешенной с помощью стальной проволоки 2 к кронштейнам 3 и 4. На кронштейне 5 закреплена стальная плита, которая служит основанием фотоэлектрическому датчику 7 и угловой шкале 8. Электромагнит 7 может изменять положение на плите, а его положение относительно фотоэлектрического датчика указывает по угловой шкале стрелка 9, притягиваемая к электромагниту. Фотоэлектрический датчик и электромагнит соединены электронным секундомером 11.
маятник состоит из рамки 1, подвешенной с помощью стальной проволоки 2 к кронштейнам 3 и 4. На кронштейне 5 закреплена стальная плита, которая служит основанием фотоэлектрическому датчику 7 и угловой шкале 8. Электромагнит 7 может изменять положение на плите, а его положение относительно фотоэлектрического датчика указывает по угловой шкале стрелка 9, притягиваемая к электромагниту. Фотоэлектрический датчик и электромагнит соединены электронным секундомером 11.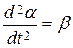 запишется следующим образом:
запишется следующим образом: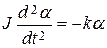 или
или 
 , (2)
, (2) , (3)
, (3) . (4)
. (4) . (5)
. (5)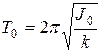 , (6)
, (6) . (7)
. (7) . (8)
. (8) . (9)
. (9)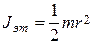 , где m – масса цилиндра. Масса эталонных тел указана с точностью Dm= 0.1 г, а геометрические размеры цилиндра измеряются штангенциркулем.
, где m – масса цилиндра. Масса эталонных тел указана с точностью Dm= 0.1 г, а геометрические размеры цилиндра измеряются штангенциркулем. . (10)
. (10)


