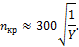Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Расчет валов и осей на крутильную жесткость.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Максимальный угол закручивания определяется также по формулам курса "Сопротивление материалов".
Допускаемый угол закрутки в градусах на метр длины можно принимать равным:
Допускаемые упругие перемещения зависят от конкретных требований к конструкции и определяются в каждом отдельном случае. Так, например, для валов зубчатых цилиндрических передач допустимая стрела прогиба под колесом Малое значение допускаемых перемещений иногда приводит к тому, что размеры вала определяет не прочность, а жесткость. Тогда нецелесообразно изготовлять вал из дорогих высокопрочных сталей. В целях упрощения расчетов можно пользоваться готовыми формулами, рассматривая ось или вал как тела, имеющие постоянное сечение приведенного диаметра. Такие формулы имеются в справочной и учебной литературе (см. курс «Сопротивление материалов»). Расчет на жесткость производят только после расчета вала или оси на прочность, когда форма и размеры известны. Потребная крутильная жесткость валов определяется различными критериями. Статические упругие угловые деформации кинематических цепей могут сказываться на точность работы машины: например, точных зуборезных станков, делительных машин и т.д. В связи с этим углы закручивания длинных ходовых валов тяжелых станков ограничиваются величиной φ = 51 на длине 1 м. Для вала-шестерни недостаточная крутильная жесткость может привести к увеличенной концентрации нагрузки по длине зуба. Для большинства валов жесткость на кручение существенного значения не имеет и расчет на крутильную жесткость не производят. Когда же деформация кручения валов должна быть ограничена, то валы рассчитывают на жесткость при кручении по формулам сопротивления материалов. Расчет валов на колебания Для большинства быстроходных валов причинами, вызывающими колебания являются силы от неуравновешенных масс деталей. При совпадении или кратности частоты возмущающей силы и частоты собственных колебаний вала наступает явление резонанса, при котором амплитуда колебаний вала резко возрастает и может достигнуть опасных значений. Соответствующие резонансу угловую скорость (ω) и частоту вращения (n) называют критическими (ω кр,nкр). Различают следующие виды колебаний валов: поперечные или изгибные угловые или крутильные; и изгибно-крутильные. В курсе ДМ рассматривают только поперечные колебания, а остальные – в специальных курсах. Расчет осей и валов на поперечные колебания заключается в проверке условия отсутствия резонанса при установившемся режиме.
Рис.14.1. Схема для определения критической частоты вращения вала Исследованиями установлено, что для отсутствия явления резонанса скорость вращения оси или вала при установившемся движении должна быть меньше или больше критической скорости.
где Y – прогиб вала от действия веса установленных на нем деталей. Например, для простейшей схемы, когда на валу симметрично относительно опор установлена деталь, весом (Р) со смещенным центром тяжести на величину (е). Для этого случая
Критическое число оборотов равно:
О приближении скорости вращения вала к критической можно судить по появлению увеличивающейся вибрации вала. Большинство валов и осей работают в докритической области. Для уменьшения опасности резонанса повышают жесткость валов и уменьшают их частоту вращения n ≤ 0,7 n кр. При больших скоростях вращения применяют валы (турбины, центрифуги), работающие в закритической области. Сами валы изготавливают повышенной податливости, кроме того, принимают n ≥ 0,7 n кр. Переход через ω кр осуществляют возможно быстрее и предусматривают специальные ограничители колебаний.
1.7 Опоры качения, выбор.
По найденному коэффициенту работоспособности подшипника определяют его размеры по таблицам ГОСТ на данный тип подшипника. Величина условной радиальной нагрузки Q зависит от типа подшипника. В случае радиальных шарико- и роликоподшипников условная радиальная нагрузка определяется по эмпирической формуле Q = (Rkк + mA)kбkТ где R — действительная радиальная нагрузка в кг; Условная радиальная нагрузка для упорных подшипников определится по формуле Q = AkбkТ При действии на радиально-упорный подшипник радиальной нагрузки возникает дополнительная осевая сила, разгружающая подшипник в осевом направлении. Если вал смонтирован на двух радиально-упорных подшипниках, имеющих одинаковые радиальные нагрузки, то их осевые силы взаимно уничтожаются. В этом случае условная радиальная нагрузка на радиально-упорные подшипники будет определяться по формуле для радиальных подшипников Q = (Rkк + mA)kбkТ Если осевые силы не уравновешиваются, то условная радиальная нагрузка должна определяться по формуле Q = QпрkкkбkТ где Qпр — приведенная радиальная нагрузка. Величина Qпр для разных случаев установки и нагружения подшипников в специальных таблицах.
Другой пример выбора Определение радиальных реакций. Вал на подшипниках, установленных по одному в опоре, условно рассматривают как балку на шарнирно-подвижных опорах или как балку с одной шарнирно-подвижной и одной шарнирно-неподвижной опорой. Радиальную реакцию Fr подшипника считают приложенной к оси вала в точке пересечения с ней нормалей, проведенных через середины контактных площадок. Для радиальных подшипников эта точка расположена на середине ширины подшипника. Для радиально-упорных подшипников расстояние а между этой точкой и торцом подшипника может быть определено графически (рис. 25) или аналитически: a=0,5[B+0,5(d+D))tgα]; подшипники роликовые конические однорядные a=0,5(T+(d+D)е/з]. Ширину В кольца, монтажную высоту Т, коэффициент е осевого нагружения, угол
Рис.25.Расположение точки приложения α контакта, а также диаметры d и D принимают по каталогу. В ряде случаев направление вращения может быть переменным или неопределенным, причем изменение направления вращения может привести к изменению не только направления, но и значений реакций опор. При установке на концы валов соединительных муфт направление силы на вал от муфты неизвестно. В таких случаях при расчете реакций рассматривают наиболее опасный вариант. Возможная ошибка при этом приводит к повышению надежности. При определении осевых сил, нагружающих радиально-упорные подшипники регулируемых типов, следует учитывать осевые силы, возникающие под действием радиальной нагрузки Fr вследствие наклона контактных линий. Значения этих сил зависят от типа подшипника, угла контакта, значений радиальных сил, а также от того, как отрегулированы подшипники (см. рис. 22, а-в). Если подшипники собраны с большим зазором, то всю нагрузку воспринимает только один или два шарика или ролика (рис. 22, а). Осевая составляющая нагрузки при передаче ее одним телом качения равна Frtg α. Условия работы подшипников при таких больших зазорах неблагоприятны, и поэтому такие зазоры недопустимы. Обычно подшипники регулируют так, чтобы осевой зазор при установившемся температурном режиме был бы близок к нулю. В этом случае под действием радиальной нагрузки Fr находятся около половины тел качения (рис. 22, 6), а суммарная по всем нагруженным телам качения осевая составляющая из-за наклона контактных линий равна е' Fr и представляет собой минимальную осевую силу, которая должна действовать на радиально-упорный подшипник при заданной радиальной силе: F a min = е' Fr (24) Для шариковых радиально-упорных подшипников с углом контакта а < 18°, F a min = е' Fr, где е' - коэффициент минимальной осевой нагрузки. В подшипниках такого типа действительный угол контакта отличается от начального и зависит от радиальной нагрузки Fr и базовой статической грузоподъемности Сor - Поэтому коэффициент е' определяют по формулам: е'= 0,563(F r/Cor) 0,195; (25) для подшипников с углом контакта а = 15° е'= 0,579(F r/Cor) 0,136; (26) Для шариковых радиально-упорных подшипников с углом контакта а ≥ 18°, е'= e и F a min = е' Fr. Значениякоэффициента е осевого нагруженияпринимают по таблице 64.
Кроме того, должно быть выполнено условие равновесия вала - равенство нулю суммы всех осевых сил, действующих на вал. Например, для схемы FA + FA1 _ FA2= О. Подбор подшипников Основной критерий работоспособности и порядок подбора подшипников зависит от значения частоты вращения кольца. Подшипники выбирают по статической грузоподъемности, если они воспринимают внешнюю нагрузку в неподвижном состоянии или при медленном вращении
|
||||||
|
Последнее изменение этой страницы: 2016-04-07; просмотров: 672; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.116.15.124 (0.008 с.) |

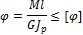

 , где т – модуль зацепления.
, где т – модуль зацепления.