
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Определение числа зубьев шестерни и колеса по суммарному числу зубьев передачи и известному передаточному числу.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Если известно uи z1= где z1 — число зубьев шестерни; z2 — число зубьев колеса;
Рис. 32 Рис. 33
Расчет зубьев цилиндрической прямозубой передачи на изгиб По международному стандарту ISO / DIS 6336: (Ausgabe 1986) по расчету зубчатых передач предусмотрены четыре метода расчета зубчатых передач. Метод А – экспериментально – исследовательский требует точных измерений, обширного и трудоёмкого математического анализа или обоснования на основе надежного эксплуатационного эксперимента на подобных приводах. При этом предел выносливости и эквивалентное окружное усилие или коэффициент внешней динамики – К А определяется из полученного измерением коллектива нагрузок с использованием гипотез накопления повреждений. Поскольку величина К А может принять весьма большие значения от 1 до 2 и более, то применяемый метод расчета и величина К А должны согласовываться между изготовителем и покупателем редуктора. Как видим, метод очень дорог и применяется крайне редко. Метод В - экспериментально- теоретический и производится на основе исследования предела выносливости зубчатого колеса – представителя, считается целесообразным для зубчатых передач массового производства. Метод С - приближенный, при этом аналитический расчет производится на основе комплексных данных стандарта или справочной технической литературы. Метод D – упрощенный, примерно соответствует приводимому расчету данного раздела. Необходимо заметить, что метод расчета зубчатых передач по ГОСТу 21354-87 занимает промежуточное положение между методами С и D. В методе С коэффициент формы зуба при расчете на изгиб рассматривается как произведение двух переменных (YFS=YF∙YS). Ниже излагается упрощенный метод расчета зуба на изгиб, основанный на положениях сопротивления материалов. На рис. 34 показаны схема зацепления двух зубьев в полюсе и силы, действующие на зубья колес со стороны шестерни; трение не учитывается. Нормальная сила Fn раскладывается на две составляющие: окружную силу Ft и радиальную или распорную — Fr.
Рис. 34. Усилия в зацеплении прямозубой цилиндрической передачи
При выводе формул принимают следующие упрощения и допущения: зуб рассматривают как консольную балку прямоугольного сечения, работающую на изгиб и сжатие; вся нагрузка, действующая в зацеплении, передается одной парой зубьев и приложена к их вершинам; нагрузка равномерно распределена по длине зуба На рис.35 показан профиль балки равного сопротивления (s — толщина зуба в опасном сечении; l — плечо изгибающей силы;
Рис.35. Схема расчета зубьев на изгиб
Определим силы в опасном сечении корня зуба. Разложим силу Fn в точке А на две составляющие: Сила
где Исходя из изложенного выше, за расчетное напряжение принимают напряжения на растянутой стороне зуба:
Для опасного сечения ВС условие прочности
где σF — напряжение изгиба в опасном сечении корня зуба; W — осевой момент сопротивления; A= Выразим I и s в долях модуля зубьев: l = km; s = cm, где к и с — коэффициенты, зависящие от формы зуба, т.е. от угла Тогда изгибающий момент в опасном сечении MB=Ft∙ l =Ft∙km; осевой момент сопротивления прямоугольного сечения зуба
Подставим в формулу (2) входящие в него параметры МИ и W, введем коэффициенты расчетной нагрузки В результате получим окончательную формулу проверочного расчета прямозубой передачи на усталость при изгибе
где YF — коэффициент учитывающий форму зуба и концентрацию напряжений (табл. 8).
Выведем формулу проверочного расчета прямозубых передач на усталость при изгибе через вращающий момент Т2.. С учетом того, что Ft=2T1/d1=2T1/mz1=2T2/mz1u;
где
Из формул (5) и (6) получаем формулы проектировочного расчета на изгиб P1=T1
где Km = 1,4 для прямозубых колес. В формулу (8) подставляют меньшее из двух отношений Выбор допускаемых напряжений изгиба. Выше отмечалось, что причиной поломки зубьев, как правило, является усталость материала под действием повторных переменных изгибающих напряжений. Поэтому значения допускаемых напряжений должны быть определены исходя из предела выносливости зубьев. Допускаемое напряжение изгиба определяют по формуле
где В зависимости от твердости активных поверхностей зубьев коэффициент долговечности YN определяется по следующим формулам:
где
где
где LГ — срок службы передачи, год; С — число смен; tc — продолжительность смены, ч; kГ — коэффициент годового использования привода; kс — коэффициент использования привода в смене. Формула (12) приемлема для определения расчетной циклической долговечности только при постоянном режиме нагрузки. При выборе материала для зубчатой пары с целью сокращения номенклатуры, как правило, назначают одинаковые материалы. Разность значений твердостей для шестерни и колеса достигается их термической обработкой. Получение нужных механических характеристик зависит не только от температурного режима обработки, но и от размеров заготовки. При переменном режиме нагрузки расчетная циклическая долговечность определяется по формуле:
где KFE — коэффициент приведения переменного режима нагрузки к постоянному эквивалентному режиму:
где T max, Тi — максимальные и промежуточные значения моментов; коэффициент mF = 6 — при нормализации и улучшении; mF =9 — при закалке; ti — продолжительность (в часах) действия момента Тi; Расчет цилиндрической прямозубой передачи на контактную прочность Расчет прочности контактирующих поверхностей зубьев основан на ограничении наибольших нормальных напряжений. При выводе формул приняты следующие допущения: зубья рассматривают как два находящихся в контакте цилиндра с параллельными образующими (радиусы этих цилиндров принимают равными радиусам кривизны профилей зубьев в полюсе зацепления); нагрузку считают равномерно распределенной по длине зуба; контактирующие профили предполагают неразделенными масляной пленкой. На основании этих допущений к расчету зубчатых колес можно применить результаты исследований на контактную прочность цилиндрических роликов. Наибольшие нормальные контактные напряжения возникают в точках, лежащих на очень малой глубине под линией контакта по формуле Герца—Беляева:
где q — расчетная удельная нормальная нагрузка; Eпр — приведенный модуль упругости материалов зубьев;
где Для учета неравномерности распределения нагрузки по длине контактных линий, а также для учета динамических нагрузок вследствие погрешности изготовления и деформации деталей передачи вводят коэффициент нагрузки Отсюда
Приведенный модуль упругости Епр=2Е1Е2/(Е1+Е2), где E1 и E2 — модули упругости материалов шестерни и колеса. Зубья рассматриваются как цилиндры длиной ba (ширина зубчатого колеса) и радиусов
Приведенный радиус кривизны зубьев в полюсе
Здесь знак «плюс» для внешнего зацепления, знак «минус» — для внутреннего зацепления. Подставляя значения ρпр и q в формулу (17), после преобразований получим
Обозначим в формуле (19) выражение
материалов сопряженных колес (ZM= 275 МПа1/2 — для стальных колес);
Получим расчетную формулу, рекомендуемую для проверочного расчета:
После подстановки значений Ft=2T2/d1u; d1=2
Значение ψba определяют по формуле После некоторых преобразований формулы (21) получим формулу проектировочного расчета для определения межосевого расстояния прямозубых зубчатых передач:
Обозначим Ka (для прямозубых передач при KHV= 1,25, Ka= 49,5 МПа1/3). Тогда формула проектного расчета для определения межосевого расстояния закрытых цилиндрических передач
Допускаемые контактные напряжения (МПа) при расчете рабочих поверхностей на усталостное выкрашивание рассчитываются по формуле
Где SH — коэффициент безопасности (SH= 1,1 при нормализации, улучшении или объемной закалке; при поверхностной закалке и цементации SH=1,2); ZR — коэффициент, учитывающий шероховатость сопряженных поверхностей зубьев (ZR=1 KHL — коэффициент долговечности, который учитывает влияние срока службы, режима нагрузки передачи и возможность повышения допускаемых напряжений для кратковременно работающих передач. При постоянной нагрузке При переменной нагрузке расчетная циклическая долговечность определяется по формуле:
где КНЕ — коэффициент приведения переменного режима нагружения к постоянному эквивалентному
В расчетные формулы (21) и (22) входит меньшее из допускаемых напряжений, установленных для шестерни и колеса. Так как материал колеса имеет обычно меньшую твердость, чем материал шестерни, то в большинстве случаев
1.6 Оси и валы. Расчеты.
Валом называют деталь (как правило, гладкой или ступенчатой цилиндрической формы), предназначенную для поддержания установленных на ней шкивов, зубчатых колес, звездочек, катков и т. д., и для передачи вращающего момента. При работе вал испытывает изгиб и кручение, а в отдельных случаях помимо изгиба и кручения валы могут испытывать деформацию растяжения (сжатия). Некоторые валы не поддерживают вращающиеся детали и работают только на кручение (карданные валы автомобилей, валки прокатных станков и др.). Вал 1 (рис.1) имеет опоры 2, называемые подшипниками. Часть вала, охватываемую опорой, называют цапфой. Концевые цапфы именуют шипами 3, а промежуточные — шейками 4.
Рис.1. Прямой вал: 1 — вал; 2 — опоры вала; 3 — цапфы; 4 — шейка Осью называют деталь, предназначенную только для поддержания установленных на ней деталей. В отличие от вала ось не передает вращающего момента и работает только на изгиб. В машинах оси могут быть неподвижными или же могут вращаться вместе с сидящими на них деталями (подвижные оси). Не следует путать понятия "ось колеса", это деталь и "ось вращения", это геометрическая линия центров вращения. Примером вращающейся оси могут служить оси железнодорожного подвижного состава, примером не вращающихся – оси передних осей автомобиля.
Рис.2. Конструкции осей:
Формы валов и осей весьма многообразны от простейших цилиндров до сложных коленчатых конструкций На первом этапе (предварительный) при отсутствии данных об изгибающих моментах определяют диаметр вала по известному крутящему моменту из условия прочности по заниженным касательным напряжениям
где [τ]=12…20 МПа – допускаемое напряжение на кручение.
|
||||
|
Последнее изменение этой страницы: 2016-04-07; просмотров: 3619; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.116.24.148 (0.009 с.) |

 , то число зубьев шестерни и колеса можно определить по формулам:
, то число зубьев шестерни и колеса можно определить по формулам:

 .
.

 и
и  , условно принимаем, что сила Fn приложена только к одному зубу (перекрытием пренебрегаем), а сила Ft равна окружной силе на начальной окружности.
, условно принимаем, что сила Fn приложена только к одному зубу (перекрытием пренебрегаем), а сила Ft равна окружной силе на начальной окружности.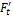 изгибает зуб, а сила
изгибает зуб, а сила  ;
;  ; Fn-Ft/cos
; Fn-Ft/cos  (1)
(1)

 (табл. 6), KFV (табл. 7) и теоретический коэффициент концентрации напряжений КТ.
(табл. 6), KFV (табл. 7) и теоретический коэффициент концентрации напряжений КТ.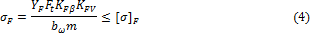
 mz1формула проверочного расчета (4) примет вид
mz1формула проверочного расчета (4) примет вид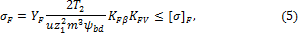
 ,
,  ,МПа; m, мм; T2 — вращающий момент на колесе, Нмм; Z1 — число зубьев шестерни;
,МПа; m, мм; T2 — вращающий момент на колесе, Нмм; Z1 — число зубьев шестерни;  ; (6)
; (6)


 — базовый предел выносливости зубьев при отнулевом цикле изменения напряжений (табл. 10); SF — коэффициент безопасности (SF = 1,7
— базовый предел выносливости зубьев при отнулевом цикле изменения напряжений (табл. 10); SF — коэффициент безопасности (SF = 1,7  2,2; SF > 2,2 — для литых заготовок); YR — коэффициент, учитывающий шероховатость поверхности зуба (YR= 1,05
2,2; SF > 2,2 — для литых заготовок); YR — коэффициент, учитывающий шероховатость поверхности зуба (YR= 1,05  при НВ
при НВ  350, (10)
350, (10) при НВ
при НВ  350, (11)
350, (11)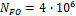 — число циклов соответствующее точке перелома кривой усталости; N F — расчетная циклическая долговечность;
— число циклов соответствующее точке перелома кривой усталости; N F — расчетная циклическая долговечность; , (12)
, (12) — частота вращения (угловая скорость) шестерни или колеса, об/мин (рад/с); с — число колес, находящихся в зацеплении с рассчитываемым колесом;
— частота вращения (угловая скорость) шестерни или колеса, об/мин (рад/с); с — число колес, находящихся в зацеплении с рассчитываемым колесом;  — продолжительность работы зубчатой передачи за расчетный срок службы, ч;
— продолжительность работы зубчатой передачи за расчетный срок службы, ч; , (13)
, (13) ,(14)
,(14)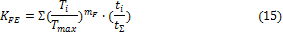
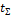 — суммарная продолжительность работы зубчатой передачи.
— суммарная продолжительность работы зубчатой передачи.
 — приведенный радиус кривизны профилей зубьев шестерни и колеса;
— приведенный радиус кривизны профилей зубьев шестерни и колеса;  — коэффициент Пуассона. Для прямозубых колес без учета коэффициентов нагрузки
— коэффициент Пуассона. Для прямозубых колес без учета коэффициентов нагрузки , (17)
, (17) — нормальная сила, действующая на зуб (см. рис. 35); Ft — окружная сила;
— нормальная сила, действующая на зуб (см. рис. 35); Ft — окружная сила;  — суммарная длина контактной линии (для прямозубых передач;
— суммарная длина контактной линии (для прямозубых передач;  — ширина венца, так как
— ширина венца, так как  ; здесь
; здесь  — коэффициент, учитывающий непостоянство суммарной длины контактной линии);
— коэффициент, учитывающий непостоянство суммарной длины контактной линии);  — коэффициент перекрытия.
— коэффициент перекрытия.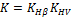 (см. табл. 6-7).
(см. табл. 6-7).
 и
и  , где
, где


 через ZH — коэффициент, учитывающий форму сопряженных поверхностей зубьев;
через ZH — коэффициент, учитывающий форму сопряженных поверхностей зубьев; — коэффициент, учитывающий механические свойства
— коэффициент, учитывающий механические свойства — коэффициент, учитывающий суммарную длину контактных линии для (
— коэффициент, учитывающий суммарную длину контактных линии для ( ) прямозубых передач.
) прямозубых передач.
 и
и 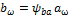 в формулу (20) и некоторых преобразований получим удобную для расчета формулу
в формулу (20) и некоторых преобразований получим удобную для расчета формулу
 (
(
 через вспомогательный коэффициент
через вспомогательный коэффициент
 ,
, — предел выносливости рабочих поверхностей зубьев (табл. 11), соответствующий базовому числу циклов перемены напряжений NHlim, МПа (база испытаний NH0 определяется по табл. 12);
— предел выносливости рабочих поверхностей зубьев (табл. 11), соответствующий базовому числу циклов перемены напряжений NHlim, МПа (база испытаний NH0 определяется по табл. 12); ;
;  (или
(или  ) — циклическая долговечность.
) — циклическая долговечность. ,
,
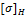 для колеса меньше.
для колеса меньше.





