Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
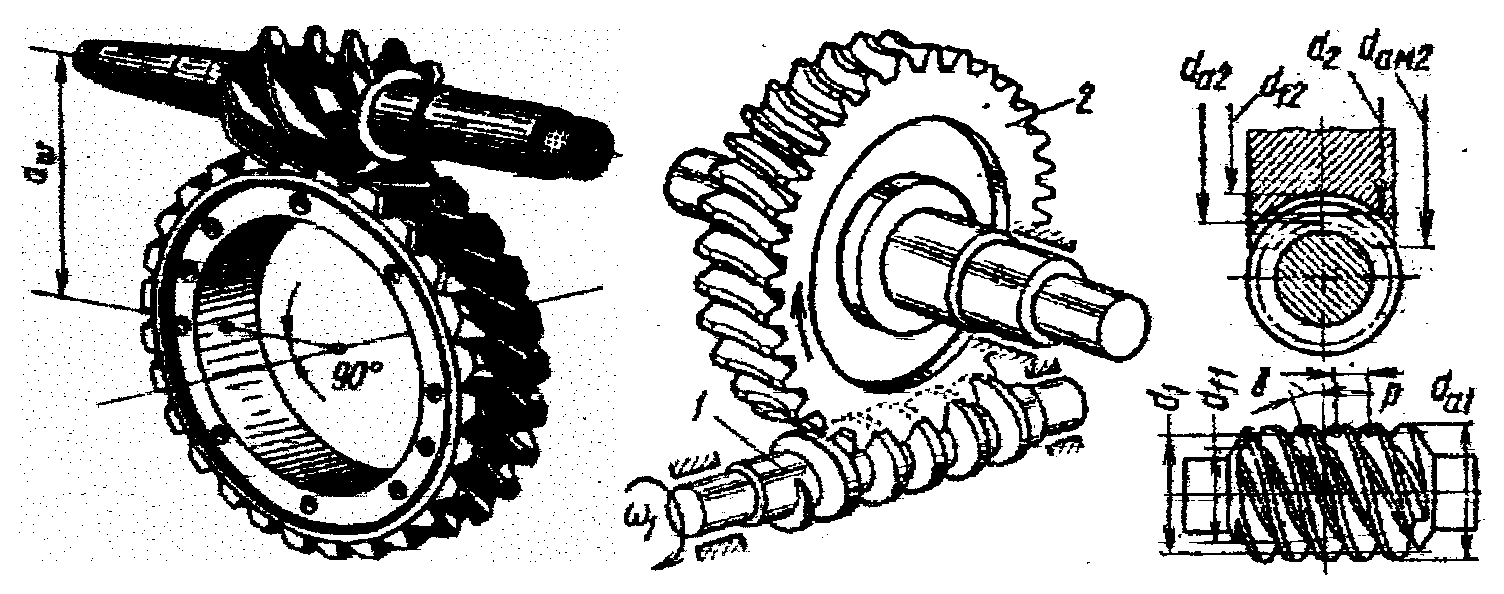
Конические зубчатые передачиСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте Передают вращающий момент между валами с пересекающимися осями (чаще всего под углом 900). Их зубья бывают прямыми, косыми, круговыми и обычно имеют эвольвентный профиль. И хотя, конические колёса сложнее цилиндрических как по своей геометрии, так и в изготовлении, принципы силового взаимодействия, условия работы, а следовательно, и методика расчёта аналогичны цилиндрическим. Здесь мы рассмотрим только отличительные особенности расчёта конических колёс. Сначала конструктор выбирает внешний окружной модуль mte, из которого рассчитывается вся геометрия зацепления, в частности, нормальный модуль в середине зуба mnm= mte (1 – 0,5 b/Re ), где Re – внешнее конусное расстояние. Силы в конической передаче действуют аналогично цилиндрической, однако следует помнить, что из-за перпендикулярности осей радиальная сила на шестерне аналогична осевой силе для колеса и наоборот, а окружная сила при переходе от шестерни к колесу только меняет знак
В эквивалентных цилиндрических колёсах [32] диаметр начальной окружности и модуль соответствуют среднему сечению конического зуба, вместо межосевого расстояния берётся среднее конусное расстояние [45], а профили эквивалентных зубьев получают развёрткой дополнительного конуса на плоскость.
Расчёт закрытой конической зубчатой передачи
Проектный расчёт. Основной габаритный размер передачи - делительный диаметр колеса по внешнему торцу - рассчитывают по формуле [1]:
где Епр - приведённый модуль упругости, для стальных колёс Епр =Естали= =2,1105 МПа; T2 - вращающий момент на валу колеса, Нмм; KH - коэффициент неравномерности распределения нагрузки по длине зуба Здесь Кbe - коэффициент ширины зубчатого венца относительно внешнего конусного расстояния, Наиболее распространено в редукторостроении значение Кbe = 0,285, тогда предыдущее выражение для определения делительного диаметра по внешнему торцу колеса принимает вид
где up – расчетное передаточное число конической передачи. Геометрический расчёт. Определяют диаметр шестерни по внешнему торцу Число зубьев шестерни По значению
Вычисленное значение z1 округляют до целого числа. Определяют число зубьев колеса Вычисленное значение - передаточное число передачи - угол делительного конуса колеса - угол делительного конуса шестерни - внешний окружной модуль Рекомендуется округлить Рассчитывают величину внешнего конусного расстояния передачи (рис.2.4) Рабочая ширина зубчатого венца колеса Полученное значение Определяют расчётный модуль зацепления в среднем сечении зуба
При этом найденное значение Рассчитывают внешнюю высоту головки зуба Внешнюю высоту ножки зуба определяют как Внешний диаметр вершин зубьев колёс рассчитывают по формуле
Угол ножки зуба рассчитывают по формуле
Проверочный расчёт. При расчёте на выносливость зубьев колёс по контактным напряжениям проверяют выполнение условия
где Eпр -приведённый модуль упругости, для стальных колёс Eпр = Eстали = =2,1105 МПа;
здесь
Далее проверяют зубья колёс на выносливость по напряжениям изгиба по формулам [1]:
где
ЧЕРВЯЧНЫЕ ПЕРЕДАЧИ
Движение в червячной передаче преобразуется по принцпу винтовой пары. Изобретателем червячных передач считают Архимеда.
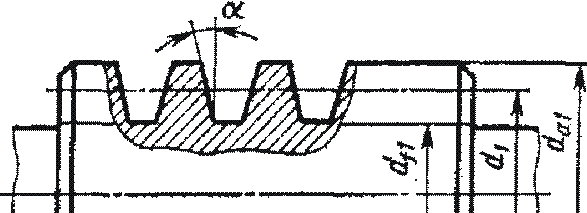
Достоинства червячных передач: + большое передаточное отношение (до 80); + плавность и бесшумность хода. В отличие от эвольвентных зацеплений, где преобладает контактное качение, виток червяка скользит по зубу колеса. Следовательно, червячные передачи имеют "по определению" один фундаментальный недостаток: высокое трение в зацеплении. Это ведёт к низкому КПД (на 20-30% ниже, чем у зубчатых), износу, нагреву и необходимости применять дорогие антифрикционные материалы. Кроме того, помимо достоинств и недостатков, червячные передачи имеют важное свойство: движение передаётся только от червяка к колесу, а не наоборот. Никакой вращающий момент, приложенный к колесу, не заставит вращаться червяк. Именно поэтому червячные передачи находят применение в подъёмных механизмах, например в лифтах. Там электродвигатель соединён с червяком, а трос пассажирской кабины намотан на вал червячного колеса во избежание самопроизвольного опускания или падения. Это свойство не надо путать с реверсивностью механизма. Ведь направление вращения червяка может быть любым, приводя либо к подъёму, либо к спуску той же лифтовой кабины. Передаточное отношение червячной передачи находят аналогично цилиндрической U = n1 / n2 = Z2 / Z1. Здесь Z2 – число зубьев колеса, а роль числа зубьев шестерни Z1 выполняет число заходов червяка, которое обычно бывает равно 1, 2, 3 или 4. Очевидно, что однозаходный червяк даёт наибольшее передаточное отношение, однако наивысший КПД достигается при многозаходных червяках, что связано с уменьшением трения за счёт роста угла трения.
Основные причины выхода из строя червячных передач: r поверхностное выкрашивание и схватывание; r излом зуба. Это напоминает характерные дефекты зубчатых передач, поэтому и расчёты проводятся аналогично [44]. В осевом сечении червячная пара фактически представляет собой прямобочное реечное зацепление, где радиус кривизны боковой поверхности "рейки" (винта червяка) r1 равен бесконечности и, следовательно, приведённый радиус кривизны равен радиусу кривизны зуба колеса rпр = r2.
Особенность расчёта на изгиб состоит в том, что принимается эквивалентное число зубьев Zэкв = Z2 / cos3g, где g - угол подъёма витков червяка. Вследствие нагрева, вызванного трением, червячные передачи нуждаются также и в тепловом расчёте. Практика показывает, что механизм опасно нагревать выше 95оС. Допускаемая температура назначается 65 oC. Уравнение для теплового расчёта составляется из баланса тепловой энергии, а именно: выделяемое червячной парой тепло должно полностью отводиться в окружающую среду Qвыделяемое = Qотводимое. Решая это уравнение, находим температуру редуктора, передающего заданную мощность N t = [ 860 N (1- η )] / [ KT S (1- Ψ )] + to. где KT – коэффициент теплоотдачи, S – поверхность охлаждения (корпус), to – температура окружающей среды, Y – коэффициент теплоотвода в пол. В случае, когда расчётная температура превышает допускаемую, то следует предусмотреть отвод избыточной теплоты. Это достигается оребрением редуктора, искусственной вентиляцией, змеевиками с охлаждающей жидкостью в масляной ванне и т.д.
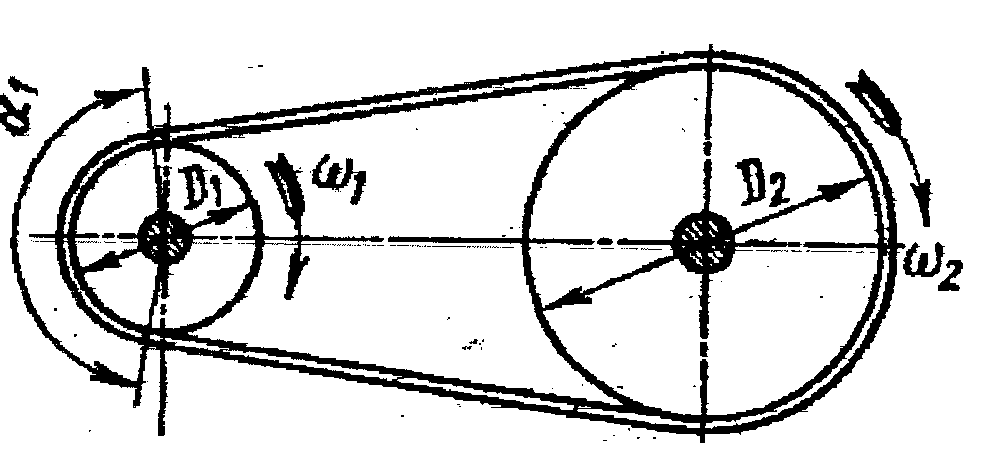
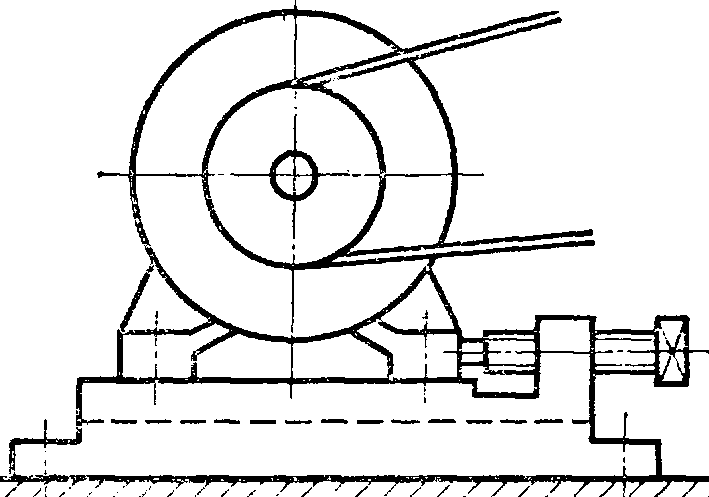
ФРИКЦИОННЫЕ ПЕРЕДАЧИ Передают движение за счёт сил трения (лат. frictio – трение). Простейшие передачи состоят из двух цилиндрических или конических роликов - катков.
Передаточное отношение цилиндрической фрикционной передачи определяют как отношение частот вращения или диаметров тел качения. U = n1/n2=D2 /[ D1 ( 1-e )], где ε – коэффициент скольжения (0,05 - для передач "всухую"; 0,01 – для передач со смазкой и большими передаточными отношениями). Для конической передачи – вместо диаметров берут углы конусов. Фрикционные передачи выполняются либо с постоянным, либо с регулируемым передаточным отношением (вариаторы).
Достоинства фрикционных передач: + простота тел качения; + равномерность вращения, что удобно для приборов; + возможность плавного регулирования скорости; + отсутствие мёртвого хода при реверсе передачи. Недостатки фрикционных передач: -потребность в прижимных устройствах; -большие нагрузки на валы, т.к. необходимо прижатие дисков; -большие потери на трение; -повреждение катков при пробуксовке; -неточность передаточных отношений из-за пробуксовки. Основными видами поломок фрикционных передач являются: r усталостное выкрашивание (в передачах с жидкостным трением смазки, когда износ сводится к минимуму); r износ (в передачах без смазки); r задир поверхности при пробуксовке.
Поскольку всё это следствие высоких контактных напряжений сжатия, то в качестве проектировочного выполняется расчёт по допускаемым контактным напряжениям [29]. Здесь применяется формула Герца-Беляева, которая, собственно говоря, и была выведена для этого случая. Исходя из допускаемых контактных напряжений, свойств материала и передаваемой мощности определяются диаметры фрикционных колёс
-высокая износостойкость и поверхностная прочность; -высокий коэффициент трения (во избежание больших сил сжатия); -высокий модуль упругости (чтобы площадка контакта, а значит и потери на трение были малы). Наиболее пригодными оказываются шарикоподшипниковые стали типа ШХ15 или 18ХГТ, 18Х2Н4МА.
Более надёжны передачи, у которых ведущий каток твёрже, чем ведомый, т.к. тогда при пробуксовке не образуются лыски. Применяются обрезиненные катки, однако их коэффициент трения падает с ростом влажности воздуха. Для крупных передач применяют прессованный асбест, прорезиненную ткань и кожу.
РЕМЕННЫЕ ПЕРЕДАЧИ Являются разновидностью фрикционных передач, где движение передаётся посредством специального кольцевого замкнутого ремня. Ременные передачи применяются для привода агрегатов от электродвигателей малой и средней мощности; для привода от маломощных двигателей внутреннего сгорания. Ремни имеют различные сечения: а) плоские, прямоугольного сечения; б) трапециевидные, клиновые; в) круглого сечения; г) поликлиновые. Наибольшее распространение имеют плоские и клиновые ремни. Плоские ремни применяются как простейшие, с минимальными напряжениями изгиба, а клиновые имеют повышенную тяговую способность. Клиновые ремни применяют по несколько штук, чтобы варьировать нагрузочную способность и несколько повысить надёжность передачи. Кроме того, один толстый ремень, поставленный вместо нескольких тонких будет иметь гораздо большие напряжения изгиба при огибании шкива. В лёгких передачах благодаря закручиванию ремня можно передавать вращение между параллельными, пересекающимися, вращающимися в противоположные стороны валами. Это возможно потому, что жёсткость на кручение ремней вследствие их малой толщины и малого модуля упругости мала. Достоинства ременных передач: − передача движения на средние расстояния; − плавность работы и бесшумность; − возможность работы при высоких оборотах; − дешевизна.
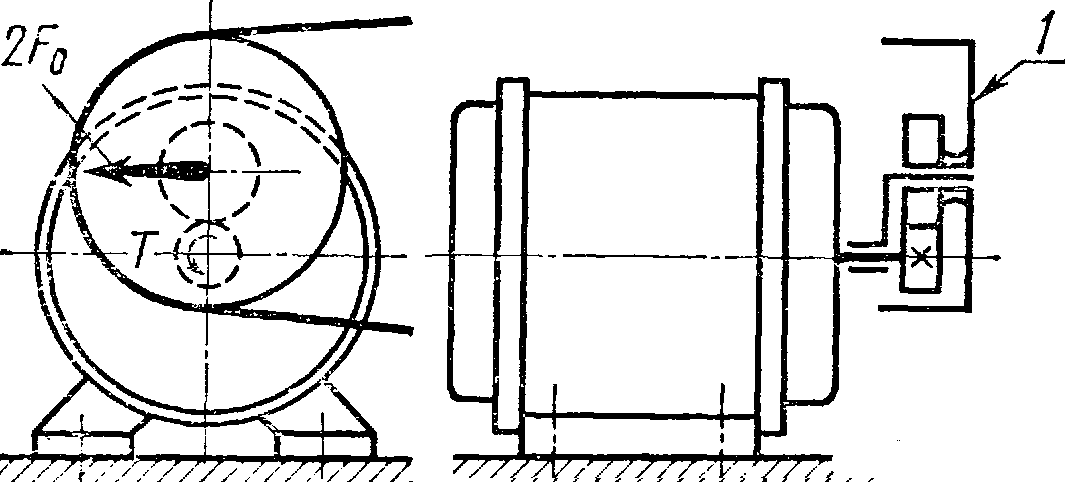
Недостатки ременных передач: - большие габариты передачи; - неизбежное проскальзывание ремня; - высокие нагрузки на валы и опоры из-за натяжения ремня; - потребность в натяжных устройствах; - опасность попадания масла на ремень; - малая долговечность при больших скоростях. Натяжение ремня существенно влияет на долговечность, тяговую способность и к.п.д. передачи. Чем выше предварительное натяжение ремня Fo, тем больше тяговая способность и к.п.д., но меньше долговечность ремня. Натяжение ремня в передачах осуществляется: ® Устройствами периодического действия, где ремень натягивается винтами. Ремень периодически подтягивается по мере вытяжки. Требуется систематическое наблюдение за передачей, иначе возможно буксование и быстрый износ ремня. ® Устройствами постоянного действия, где натяжение создаётся грузом, весом двигателя или пружиной. Часто натяжение происходит за счёт массы двигателя на качающейся плите. К таким устройствам относятся натяжные ролики. Натяжение ремня автоматически поддерживается постоянным.
® Устройствами, автоматически регулирующими натяжение в зависимости от нагрузки с использованием сил и моментов, действующих в передаче. Шкив 1 установлен на качающемся рычаге, который также является осью ведомого колеса зубчатой передачи. Натяжение ремня 2Fo равно окружной силе на шестерне и пропорционально передаваемому моменту.
|
||||||||||
|
Последнее изменение этой страницы: 2016-04-19; просмотров: 865; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.214 (0.009 с.) |

 ;
;  .
.
 Рис.2.4
Рис.2.4
 ,
, . Рекомендуют принять Кbe 0,3. Меньшие значения назначают для неприрабатываемых зубчатых колёс, когда H1 и H2 > 350 HB или V > 15 м/с.
. Рекомендуют принять Кbe 0,3. Меньшие значения назначают для неприрабатываемых зубчатых колёс, когда H1 и H2 > 350 HB или V > 15 м/с. ,
,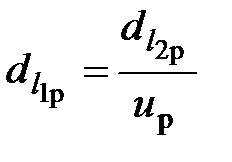 .
. назначают по рекомендациям
назначают по рекомендациям определяют число зубьев шестерни:
определяют число зубьев шестерни: при Н1 и Н2 350 HB,
при Н1 и Н2 350 HB, при Н1 45 HRC и Н2 350 HB,
при Н1 45 HRC и Н2 350 HB, при Н1 и Н2 45 HRC.
при Н1 и Н2 45 HRC. .
. округляют до целого числа. После этого необходимо уточнить:
округляют до целого числа. После этого необходимо уточнить: ,
, ,
, ,
, .
. до стандартного значения
до стандартного значения  по ряду модулей: 1,5; 2; 2,5; 3; 4; 5; 6; 8; 10. После этого уточняют величины диаметров
по ряду модулей: 1,5; 2; 2,5; 3; 4; 5; 6; 8; 10. После этого уточняют величины диаметров  и
и  .
. .
. .
. округляют до ближайшего из ряда нормальных линейных размеров (табл. 2.5).
округляют до ближайшего из ряда нормальных линейных размеров (табл. 2.5). .
. не округляют!
не округляют! .
. .
. .
. .
.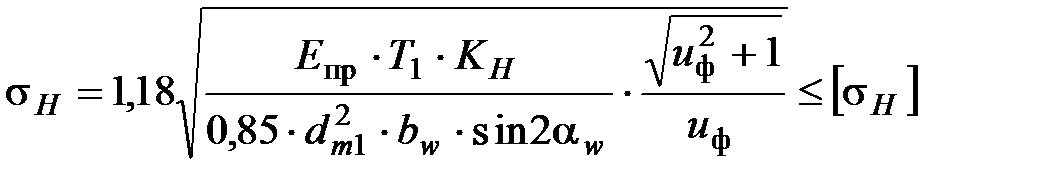 ,
, - вращающий момент на шестерне, Нмм,
- вращающий момент на шестерне, Нмм,  ;
; - кпд передачи.
- кпд передачи. - коэффициент расчётной нагрузки,
- коэффициент расчётной нагрузки, 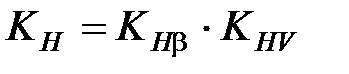 ; коэффициент концентрации нагрузки
; коэффициент концентрации нагрузки 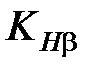 найден ранее по графикам рис.2.5.
найден ранее по графикам рис.2.5. - коэффициент динамической нагрузки, находят по табл. 2.7 с понижением на одну степень точности против фактической, назначенной по окружной скорости
- коэффициент динамической нагрузки, находят по табл. 2.7 с понижением на одну степень точности против фактической, назначенной по окружной скорости 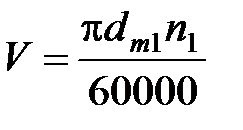 в соответствии с рекомендациями (табл.2.6);
в соответствии с рекомендациями (табл.2.6);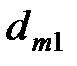 - делительный диаметр шестерни в среднем сечении зуба,
- делительный диаметр шестерни в среднем сечении зуба,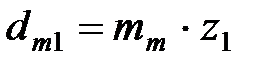 ;
; - угол зацепления,
- угол зацепления, 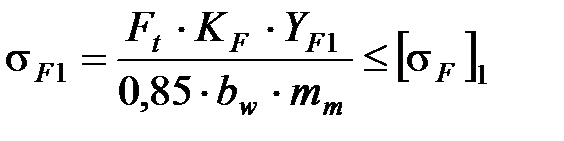 и
и  ,
, - окружное усилие в зацеплении, Н,
- окружное усилие в зацеплении, Н, 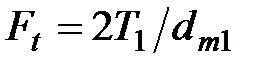 ;
; - коэффициент расчётной нагрузки,
- коэффициент расчётной нагрузки,  . Здесь
. Здесь 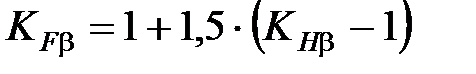 , а
, а 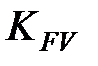 определяют по табл. с понижением точности на одну степень против фактической.
определяют по табл. с понижением точности на одну степень против фактической.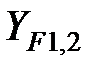 - коэффициент формы зуба соответственно шестерни и колеса, находят по табл. в зависимости от эквивалентного числа зубьев колёс
- коэффициент формы зуба соответственно шестерни и колеса, находят по табл. в зависимости от эквивалентного числа зубьев колёс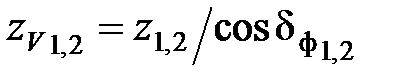 .
.

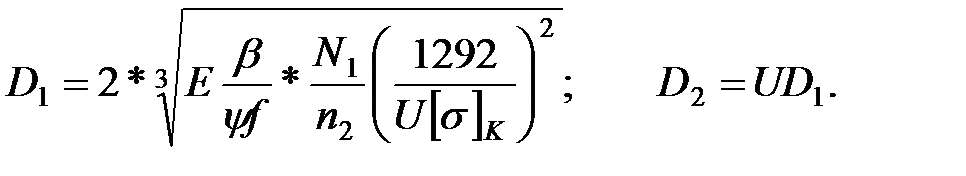
 Основные требования к материалам фрикционных колёс:
Основные требования к материалам фрикционных колёс: Разработаны специальные фрикционные пластмассы с асбестовым и целлюлозным наполнителем, коэффициент трения которых достигает 0,5. Широко применяется текстолит.
Разработаны специальные фрикционные пластмассы с асбестовым и целлюлозным наполнителем, коэффициент трения которых достигает 0,5. Широко применяется текстолит.