
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Прямозубые и косозубые цилиндрические зубчатые передачиСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
1.1. Определить диаметры вершин зубьев зубчатых колес 1.2. Найти модуль m и межосевое расстояние аw прямозубой цилиндрической передачи, если известно: число зубьев шестерни Z1=20, число зубьев колеса Z2=80, диаметр вершин зубьев 1.3. При проверке действительного межосевого расстояния зубчатой передачи по модулю m=3 мм и с числом зубьев Z1=33, Z2=64 оказалось, что 1.4. Найти приведенный радиус кривизны для прямозубой цилиндрической передачи, если известно: число зубьев Z1=35, Z2=70, модуль m=4 мм. 1.5. Определить нормальный модуль зуба в косозубой цилиндрической передаче, если известно: межосевое расстояние аw=200 мм, диаметр вершин 1.6. При расчёте соосного редуктора получилось, что межосевое расстояние тихоходной прямозубой пары аw=150 мм, (Z3+Z4) =100, для быстроходной косозубой цилиндрической пары (Z1+Z2)=99, модуль нормальный mn=3 мм. Найти величину угла наклона зуба b, при котором не будет нарушена соосность редуктора, то есть aw1 = aw2. 1.7. Найти делительные диаметры шестерни и колеса косозубой цилиндрической передачи, если межосевое расстояние aw=100 мм, число зубьев Z1=33, передаточное число u=2, угол наклона зуба b=6°6'. 1.8. Найти межосевое раcстояние эквивалентной передачи для косозубой цилиндрической передачи, если нормальный модуль mn=3 мм, диаметр вершин зубьев da1 =180,8 мм, передаточное число u=2, угол наклона зуба b=15°. 1.9. Определить нормальный и окружной модули цилиндрического косозубого колеса, если известно: диаметр вершин зубьев da1=145 мм, число зубьев Z1=27, угол наклона b=8°. 1.10. Определить потребную мощность электродвигателя привода ленточного конвейера через двухступенчатый цилиндрический редуктор, если передаваемая конвейером окружная сила Ft=5000 Н, скорость его движения V=0,6 м/с и все валы установлены на подшипниках качения. К.П.Д. пары зубчатых колес 1.11. Найти модуль прямозубой цилиндрической передачи из расчета на изгиб зуба, если известна передаваемая мощность Р=25 кВт, угловая скорость ω1=100рад/с, коэффициенты KFb=l,l; КFV=1,2; число зубьев Z1=25, 1.12. Определить передаточное число редуктора приводной станции ленточного конвейера, если скорость движения ленты V=0,6 м/с, диаметр барабана D=300 мм, частота вращения вала электродвигателя n1=940 об/мин. 1.13. Перед нами находится изношенное косозубое колесо; для его изготовления требуется определить нормальный модуль, можно измерить диаметр вершин зубьев da1, угол наклона зуба b, сосчитать число зубьев. 1.14. Определить нормальную, окружную, радиальную силы на зубе прямозубого цилиндрического колеса, если известно: мощность Р=2,5 кВт, угловая скорость ω1=25 рад/с, число зубьев Z1=25, модуль m=4 мм, угол зацепления a=20°. 1.15. Найти составляющие силы на зубе косозубой цилиндрической шестерни, если дано: мощность P1=4 кВт, угловая скорость ω1=40 рад/с, число зубьев Z1=24, нормальный модуль mn=5 мм, угол наклона зуба b=8°, угол зацепления a=20°. 1.16. Определить угол наклона зуба в косозубой цилиндрической передаче при условии: Fa = 0,1 · Ft, где Fа – осевая сила, Ft – окружная сила. Конические передачи 2.1. Найти окружную силу на зубе конической шестерни, если известно: мощность Р1=40 кВт, угловая скорость ω=40 рад/с, внешний модуль me=6 мм, коэффициент Кbе=0,25, передаточное число u=1, число зубьев Z1=25. 2.2. Найти передаточное число эквивалентной передачи, если внешнее конусное расстояние Re=200 мм, внешний модуль me=5 мм, число зубьев шестерни Z1=25. 2.3. Определить внешний окружной модуль mе конической передачи, если коэффициент Кье=0,28, длина зуба b=15 мм, числа зубьев Z1=25, Z2=50. 2.4. Найти межосевое расстояние эквивалентной передачи для конической передачи, если Z1=25, передаточное число u=2, внешний окружной модуль me=5 мм, коэффициент Кbе=0,25. 2.5. Найти осевую силу на зубе конической шестерни, если мощность P1=40 кВт, угловая скорость ω1=40 рад/с, внешний окружной модуль me=6 мм, число зубьев Z1=25, передаточное число u=1, угол зацепления a=20°, коэффициент Кbе=0,25. 2.6. Найти радиальную силу на зубе кoнической шестерни, если 2.7. Найти величину внешнего конусного расстояния конической 2.8. Найти передаточное число эквивалентной передачи uv, если известен угол начального конуса конической передачи δ1=35°. 2.9. Найти межосевое расстояние эквивалентной передачи av для конической передачи, если известно: число зубьев Z1=20, передаточное число u=3, внешний окружной модуль me=4 мм, коэффициент Кbе=0,25. 2.10. Найти средний модуль конической передачи m, если число зубьев Z1=20, Z2=40, коэффициент Кье=0,25, ширина зуба b=75 мм. 2.11. Найти диаметр делительный эквивалентной шестерни для конической шестерни, если число зубьев Z1=20, Z2=40, внешний окружной модуль me=3 мм, коэффициент Кbе=0,25. 2.12. Определить средний модуль конической передачи m, если длина зуба b=75 мм, число зубьев Z1=25, Z2=75, коэффициент Kbe=0,25. 2.13. Найти диаметр делительный эквивалентного колеса для конического колеса, если число зубьев Z1=20, передаточное число u=3, внешний модуль me=4 мм, коэффициент Кbе=0,28. 2.14. Найти межосевое расстояние эквивалентной передачи для конической передачи, если число зубьев Z1=25, передаточное число u=2, внешний модуль me=3 мм, коэффициент Kbe=0,25. 2.15. Найти величину внешнего конусного расстояния конической передачи, если de1=90 мм, u=3. 2.16. Найти окружную силу на зубе конического колеса, если мощность Р2=30 кВт, угловая скорость ω2=60 рад/с, внешний модуль me=5 мм, коэффициент Kbe=0,25, число зубьев Z1=20, передаточное число u=2, угол зацепления a=20°. 2.17. Найти осевую силу на зубе конического колеса, если мощность Р2=15 кВт, угловая скорость ω2=30 рад/с, внешний модуль me=4 мм, коэффициент Kbe=0,25, число зубьев Z1=20, передаточное число u=2, угол зацепления a=20°. 2.18. Найти окружную силу на зубе конического колеса, если мощность Р2=25 кВт, угловая скорость ω2=40 рад/с, внешний модуль me=5 мм, коэффициент Kbe=0,25, передаточное число u=2, число зубьев Z1=25. 2.19. Найти передаточное число эквивалентной передачи для конической передачи, если внешнее конусное расстояние Re=300 мм, внешний модуль me=4 мм, число зубьев Z1=20.
Червячные передачи 3.1. Определить число витков червяка, если известно, что частота вращения его n1=1440 об/мин, а червячное колесо, имеющее 48 зубьев, делает 60 об/мин. 3.2. Определить необходимый крутящий момент на валу червяка и диаметр цепного блока d3B червячной передачи грузоподъемностью Q=5000 кг. Червяк двухвитковый (m=8 мм, d1=64 мм). Червячное колесо имеет 40 зубьев. Диаметр цепной звездочки Dзв=146 мм. К.П.Д. червячной передачи h=0,75. Усилие рабочего на блоке Fp=400 Н.
3.3. Определить частоту вращения выходного вала двухступенчатого червячного редуктора при следующих данных: Z1=l, Z2=24, Z3=2, Z4=50, частота вращения входного вала червяка n1=1450 об/мин. 3.4. Найти радиальную силу червяка и колеса, если мощность Р2=20 кВт, угловая скорость ω=97 рад/с, межосевое расстояние передачи aw=140 мм, передаточное число u=30, число витков Z1=4, коэффициент диаметра q=10, коэффициент смещения Х=+0,1. 3.5. Найти начальный диаметр червяка, если межосевое расстояние червячной передачи aw=125 мм, передаточное число u=20, число витков червяка Z1=2, коэффициент диаметра q=9, коэффициент смещения Х=+0,5. 3.6. Найти требуемую поверхность охлаждения червячного редуктора, если коэффициент теплопередачи К=12 ВТ/м2 град, разность температур масла и окружающей среды 30°С, мощность червячной передачи 15 кВт, К.П.Д. червячной передачи h=0,8. 3.7. Найти окружную силу на червяке, если мощность Р1=20 кВт, угловая скорость ω1=97 рад/с, межосевое расстояние червячной передачи aw=200 мм, число витков Z1=2, передаточное число u=20, коэффициент диаметра q=9, коэффициент смещения X=+0,5, приведенный угол трения j1=2°. 3.8. Найти нормальную силу, действующую на зуб червячного колеса, если мощность Р2=25 кВт, угловая скорость ω2=97 рад/с, число зубьев червячного колеса Z2=40 модуль m=10 мм, коэффициент диаметра q=10, число витков червяка Z1=2, угол зацепления a=20°. 3.9. Найти межосевое расстояние червячной передачи, если число витков Z1=l, передаточное число u=34, коэффициент диаметра q=8, коэффициент смещения Х=+0,8, делительный диаметр колеса d2=444 мм. 3.10. Найти межосевое расстояние червячной передачи из расчета на контактную прочность бронзового колеса, работающего со стальным червяком, если Z1=l, u=60, [sн]=200 МПа, q=12, мощность Р2=35 кВт, угловая скорость ω2=97,4 рад/с, Кнb=1, KHV=1,25. 3.11. Найти скорость скольжения в червячной передаче, если модуль m=5 мм, скорость V=0,8 м/с, Z2=40, u=20, q=10. Выбрать на данной скорости скольжения допустимое контактное напряжение для колеса из бронзы БР А9ЖЗЛ, работающего со стальным червяком. 3.12. Определить К.П.Д. червячной передачи без учета потерь на трение в подшипниках и на взбалтывание масла, если модуль m=5 мм, частота вращения n1=600 об/мин, число зубьев колеса Z2=40, коэффициент диаметра q=10, передаточное число u=20. 3.13. Определить, будет ли червячная передача самотормозящейся, если коэффициент диаметра q=12, число витков Z1=l, модуль m=5 мм, частота вращения червяка n1=30 об/мин. 3.14. Найти угол подъема витка червяка, если дано межосевое расстояние червячной передачи aw=140 мм, модуль m=4,5, передаточное число u=13, число витков червяка Z1=4, коэффициент смещения Х=+0,1. 3.15. Найти передаточное число червячной передачи, если межосевое расстояние аw=125 мм, число витков Z1=2, коэффициент диаметра q=10, модуль m=5 мм. Ременные передачи 4.1. Найти геометрическую длину ремня плоскоременной передачи, если диаметр ведущего шкива D1=320 мм, передаточное число без учета упругого скольжения ремня u=3, межосевое расстояние a=4·D2. 4.2. Определить угол обхвата ремнем меньшего шкива плоскоременной открытой передачи, если диаметр ведущего шкива D1=200 мм, передаточное число без учета упругого скольжения ремня u=2,5; межосевое расстояние a=4·D2. Дать оценку работы ременной передачи. 4.3. Найти межосевое расстояние между осями валов клиноременной передачи, если угол обхвата меньшего шкива a1=120°; диаметр меньшего шкива D1=200 мм, u=6. 4.4. Плоскоременная открытая передача имеет ведущий шкив диаметром D1=225 мм, ведомый шкив диаметром D2=560 мм, длину ремня L=4650 мм, скорость ремня V=25; м/с. При проведенном расчете выяснилось, что число пробегов ремня в секунду больше допустимого. Как нужно изменить размеры межосевого расстояния и длину ремня, чтобы уменьшить число пробегов до величиныn=4 с-1? 4.5. Определить, будет ли надежно работать клиноременная передача, если известны диаметр ведущего шкива D1=100 мм, межосевое расстояние а=350 мм, передаточное число u=3. 4.6. Найти длину плоского ремня, если дано: диаметр большего шкива D2=400 мм, передаточное число u=2, угол обхвата меньшего шкива a1=160°. 4.7. Определить, будет ли надежно работать плоскоременная передача, у которой диаметры D1=100 мм, D2=300 мм, межосевое расстояние а=350 мм. 4.8. Найти фактическую угловую скорость ведомого шкива ω2, если известно: диаметр меньшего шкива D1=200 мм, коэффициент скольжения x=0,01, скорость ремня V=10 м/с, диаметр большего шкива D2=400 мм. 4.9. Найти начальное натяжение ремня, если известно: передаваемая мощность Р=4,5 кВт, скорость ремня V=45 м/с, коэффициент тяги j=0,5. 4.10. Найти натяжение ремня F1 и F2, если дано: еfb=3, мощность Р=60 кВт, скорость ремня V=12 м/с. 4.11. Определить тяговое усилие Ft, передаваемое ремнем плоскоременной передачи, если начальное напряжение s0=1,4 H/мм2, сечение ремня b·h=150 мм2, коэффициент тяги равен j=0,4. 4.12. Определить напряжение в ведущей и ведомых ветвях s1 и s2 в плоскоременной передаче, если известно: окружное усилие Ft=200 H, напряжение от центробежной силы sv=10 Н/мм2, площадь поперечного сечения А=700 мм2, F1=500 H. 4.13. Найти максимальное напряжение в ремне smax, если известно: натяжение в ведущей ветви F1=3000 H, модуль упругости Eu=80 H/мм2, площадь поперечного сечения А=230 мм2, толщина ремня d=6 мм, плотность ремня ρ=1200 кг/м3, диаметр шкива D1=300 мм, угловая скорость ω1=100 рад/с. 4.14. Определите начальное натяжение в ремне, если известно: передаваемая мощность Р=30 кВт, скорость ремня V=15 м/с, коэффициент тяги j=0,5, натяжение в ведущей ветви F1=3000 Н. 4.15. Найти ширину плоского ремня, если дано: скорость ремня V=10 м/с, передаваемая мощность Р=15 кВт, толщина ремня d=4,5 мм, допускаемая удельная сила [Р]=2 H/мм. 4.16. Найти передаваемую ремнем мощность Р и коэффициент тяги j, если дано: усилие в ведущей ветви F1=3000 Н, диаметр шкива D1=300 мм, еfb=3, ω1=100 рад/с. 4.17. Ременная передача работает при начальном напряжении s0=2 МПа с коэффициентом тяги j=0,3, сечение ремня в·h=200·5 мм, скорость ремня V=10 м/с. Найти передаваемую ремнем мощность. 4.18. Найти передаваемую ремнем мощность Р1, кВт, если известно: усилие в ведущей ветви F1=3000 H, начальное натяжение F0=2500 H, угловая скорость ω1=150 рад/с, диаметр шкива D1=200 мм. 4.19. Найти нагрузку на вал от плоскоременной передачи, если дано: угол обхвата меньшего шкива a1=160°, усилия в ведущей и ведомой ветвях F1=300 Н, F2=200 H.
Примеры решений задач по темам. Тема 1 «Прямозубые и косозубые цилиндрические зубчатые передачи». Задача: При расчёте соосного редуктора получилось, что межосевое расстояние тихоходной прямозубой пары аw=150 мм, (Z3+Z4) =100, для быстроходной косозубой цилиндрической пары (Z1+Z2)=99, модуль нормальный mn=3 мм. Найти величину угла наклона зуба b, при котором не будет нарушена соосность редуктора, то есть aw1 = aw2. Решение: Записываем формулы межосевого расстояния быстроходной и тихоходной ступеней соосного редуктора:
Так как в соосных редукторах обязательно условие равенства межосевого расстояния, то приравниваем эти два уравнения:
Отсюда: Вычислим модуль тихоходной прямозубой цилиндрической передачи:
Тема 2 «Конические передачи». Задача: Найти межосевое расстояние эквивалентной передачи для конической передачи, если Z1=25, передаточное число u=2, внешний окружной модуль me=5 мм, коэффициент Кbе=0,25. Решение: Записываем формулу для определения эквивалентного межосевого расстояния
Где Вычисляем средние делительные диаметры шестерни и колеса:
Определим внешний делительный диаметр шестерни и колеса:
Где:
Тема 3 «Червячные передачи». Задача: Найти радиальную силу червяка и колеса, если мощность Р2=20 кВт, угловая скорость ω=97 рад/с, межосевое расстояние передачи aw=140 мм, передаточное число u=30, число витков Z1=4, коэффициент диаметра q=10, коэффициент смещения Х=+0,1. Решение: Запишем формулу для определения радиальных сил на червяке и червячном колесе: Далее необходимо вычислить окружные силы: Определяем крутящие моменты на червяке и на колесе:
Вычислим делительные диаметры червяка и колеса: d1=m·q, d2=m·Z2. Через межосевое расстояние определим осевой и торцевой модули червяка и червячного колеса: Где Отсюда Тогда d1=2,15·10=21,5 мм, d2=2,15·120=258 мм.
Тема 4 «Ременные передачи». Задача: Найти длину плоского ремня, если дано: диаметр большего шкива D2=400 мм, передаточное число u=2, угол обхвата меньшего шкива a1=160°. Решение: Запишем формулу для вычисления длины ремня: Где D1=D2/U=400∙2=200 мм, Через формулу межосевого расстояния определим межосевое расстояние:
6. Вопросы к экзаменационным билетам по дисциплине. 1. Основные задачи и цели курса. 2. Основные понятия дисциплины (механизм, машина, деталь и т.п.). 3. Стандартизация, унификация деталей машин. 4. Критерии работоспособности и расчета деталей машин. 5. Проектировочный и проверочный расчет. 6. Контактная прочность деталей машин. 7. Типы соединений и их основные характеристики. 8. Заклёпочные соединения. 9. Сварные, паяные, клеевые соединения. 10. Расчет заклепочных соединений. 11. Расчет на прочность сварных, клеевых и паяных соединений. 12. Обозначение сварных швов. 13. Виды сварных соединений и типы сварных швов. 14. Резьбовые соединения, классификация резьб. 15. Геометрические и кинематические параметры резьбы. 16. Силы, возникающие в резьбе. 17. Расчет резьбовых соединений. 18. Шпоночные и шлицевые соединения. 19. Зубчатые передачи, классификация передач. 20. Основные силовые и кинематические соотношения в зубчатых передачах. 21. Эвольвентное зацепление. 22. Геометрия прямозубых зубчатых колес (основные параметры). 23. Материалы и обработка зубчатых колес. 24. Силы, действующие в зубчатом зацеплении. 25. Конические зубчатые передачи. 26. Червячные передачи. 27. Типовой расчет червячных передач. 28. Основные геометрические параметры червячного зацепления. 29. Материалы червячной пары. 30. Скорость скольжения в червячной передаче. 31. Ременные передачи. Применение, достоинства и недостатки. 32. Основные параметры ременной передачи. 33. Кинематика ременной передачи. 34. Силы и напряжения в ременной передаче. 35. Цепные передачи. Назначение, достоинства и недостатки цепных передач. 36. Основные параметры цепных передач. 37. Критерии работоспособности и расчета цепных передач. 38. Силы, действующие в цепных передачах. 39. Валы и оси. Участки валов – цапфы (шипы, шейки), гантели. Выбор диаметров посадочных поверхностей. 40. Материалы и методы изготовления валов и осей. 41. Критерии работоспособности валов и осей. 42. Предварительный расчет валов. 43. Проверочный расчет валов (на усталостную прочность). 44. Подшипники качения. 45. Классификация подшипников качения. 46. Теоретические основы расчета подшипников качения. 47. Подшипники скольжения. Виды трения, возникающие в подшипниках скольжения. 48. Муфты, типы и выполняемые функции. 49. Классификация муфт. 50. Методы подбора и расчета муфт.
|
||||
|
Последнее изменение этой страницы: 2016-04-19; просмотров: 2921; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.145.41.108 (0.008 с.) |

 ,
, 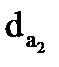 , если известно: межосевое расстояние аw=300 мм, число зубьев шестерни Z1=20, передаточное число u=5.
, если известно: межосевое расстояние аw=300 мм, число зубьев шестерни Z1=20, передаточное число u=5.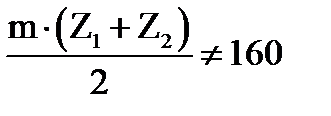 мм. Как устранить данное несоответствие?
мм. Как устранить данное несоответствие? = 0,98. К.П.Д., учитывающий потери в паре подшипников,
= 0,98. К.П.Д., учитывающий потери в паре подшипников,  =0,99.
=0,99.
 ,
, 
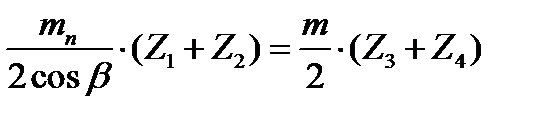
 ,
,
 β=8,10.
β=8,10.


 ,
,  .
.

 зубьев, ctgδ1=U=2, δ1=26,570.
зубьев, ctgδ1=U=2, δ1=26,570. мм,
мм,  мм,
мм, мм,
мм,  мм,
мм,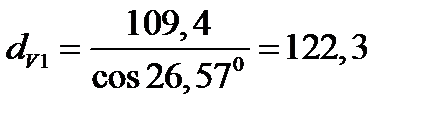 мм,
мм, 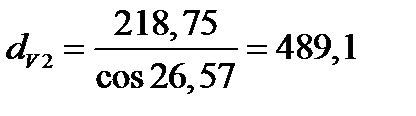 мм.
мм.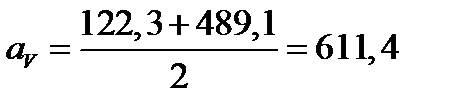 мм.
мм. ,
, 
 ,
, 

 Н·м.
Н·м. Н·м К.П.Д. принимаем в интервале 0,75…0,9.
Н·м К.П.Д. принимаем в интервале 0,75…0,9.
 зубьев.
зубьев.
 Н,
Н,  Н.
Н. Н,
Н,  Н.
Н.
 мм.
мм. тогда
тогда  .
.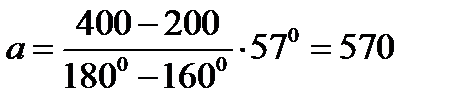 мм.
мм. мм.
мм.


