
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
И шевронных цилиндрических передачСодержание книги
Поиск на нашем сайте
У косозубых колес зубья располагаются не по образующей делительного цилиндра, а составляют с ней некоторый угол В торцовом сечении – окружной шаг – окружной модуль – делительный диаметр Прочность зуба определяют его размеры и форма в нормальном сечении. Форму косого зуба в нормальном сечении принято определять через параметры эквивалентного прямозубого колеса (рис. 4.13). Нормальное к зубу сечение образует эллипс с полуосями
где В зацеплении участвуют зубья, расположенные на малой оси эллипса, т.к. второе колесо находится на расстоянии
В соответствии с этим эквивалентное колесо будет определяться следующими параметрами: – эквивалентный диаметр
– эквивалентное число зубьев
Рис. 4.13
Эквивалентные параметры используются для распространения расчетов на прочность цилиндрических прямозубых передач на цилиндрические косозубые передачи. Увеличение эквивалентных параметров с увеличением угла
КОНИЧЕСКИЕ ЗУБЧАТЫЕ ПЕРЕДАЧИ Общие сведения Конические зубчатые передачи относятся к зубчатым передачам с пересекающимися осями. Наиболее распространены передачи с углом пересечения осей колес (межосевым углом) Пересечение осей валов конических зубчатых колес затрудняет размещение опор. Поэтому одно из конических колес, как правило, шестерню размещают консольно по отношению к опорам. Это приводит к увеличению неравномерности распределения нагрузки по ширине зубчатого венца. В конических передачах действуют значительные осевые силы, что приводит к усложнению конструкции опор.
Перечисленное выше приводит к тому, что нагрузочная способность конической прямозубой передачи составляет 85 % от нагрузочной способности цилиндрической прямозубой передачи. Конические зубчатые колеса подразделяются на колеса с прямыми и непрямыми зубьями. Основными типами колес с непрямыми зубьями являются следующие конические зубчатые колеса:
Рис. 5.1
а) колеса с тангенциальными зубьями; тангенциальный зуб направлен по касательной к некоторой воображаемой окружности радиусом
Рис. 5.2
б) колеса с эвольвентной линией зуба (продольная кривизна зуба выполнена по удлиненной эвольвенте); в) колеса с эвольвентной линией зуба (продольная кривизна зуба выполнена по удлиненной эвольвенте); г) колеса с круговыми зубьями (продольная кривизна зуба выполнена по дуге окружности); б) колеса с шевронными зубьями. Прямозубые передачи обычно применяются при небольших нагрузках и невысоких скоростях: Геометрические параметры Аналогами начальных и делительных цилиндров цилиндрических передач являются начальные и делительные конусы с углами Важнейшим геометрическим параметром конической передачи является внешнее конусное расстояние
Кроме размеров по внешнему торцу конуса, удобных для измерения и указываемых на чертежах, различают также размеры в среднем сечении (по средине зубчатого венца
Ширину зубчатого венца рекомендуется выбирать исходя из следующих условий
где Кроме окружного модуля различают также нормальный модуль
где Круговые зубья нарезают немодульным инструментом, позволяющим нарезать зубья в некотором диапазоне модулей. Поэтому в данном случае допускается применять передачи с нестандартными и дробными модулями. Для конических зубчатых передач главным образом применяется высотная коррекция для выравнивания удельных скольжений в зацеплении. Коэффициенты смещения
где Для конических передач при Как правило, для конических зубчатых передач применяют высотную коррекцию в сочетании с тангенциальной коррекцией. Применение высотной коррекции повышает износостойкость и сопротивление зубьев заеданию, тангенциальная коррекция выравнивает прочность зубьев.
Кинематические параметры Передаточное число конической зубчатой передачи определяется по формулам
Минимальное число зубьев шестерни Для уменьшения шума рекомендуется применять притирку и выбирать некратные числа зубьев колес. Если передача работает при постоянной нагрузке и умеренных линейных скоростях, то необходимо стремиться к тому, чтобы числа зубьев колес При межосевом угле
Зависимость (5.1) обычно используется для определения углов делительных конусов. Коэффициент осевого перекрытия
Для конических колес с круговым зубом предпочтителен к применению угол Угол наклона линии зуба может быть определен также по формуле
Угол
Осевая форма зуба ГОСТ 19326-73 регламентирует три основные формы конусности (изменение размеров сечений по длине зуба). При осевой форме зуба I (рис. 5.3, а) вершины делительного конуса и конуса впадин зубьев совпадают. Благодаря этому обеспечивается постоянство радиального зазора по всей длине зуба. Это позволяет увеличить радиус закругления у основания зуба и повысить его изгибную прочность. Данную форму конусности применяют для конических передач с прямыми и тангенциальными зубьями, а также для колес с круговыми зубьями при
Рис. 5.3
При осевой форме зуба II (рис. 5.3, б) вершины делительного конуса и конуса впадин зубьев не совпадают. Это обеспечивает одинаковую ширину впадины по длине зуба. При этом толщина зуба по делительному конусу растет с увеличением расстояния от вершины. Данную форму конусности применяют для конических передач с круговыми зубьями при При осевой форме зуба III (рис. 5.3, в) образующие делительного конуса, конусов вершин и впадин зубьев параллельны (равновысокие зубья, т.е. зубья не имеют конусности по высоте). Данную форму конусности применяют для конических передач с круговыми зубьями при В зубчатых колесах с зубьями формы конусности I обычно оперируют окружным модулем Силы в зацеплении Также как и в косозубой цилиндрической передаче в конической зубчатой передаче нормальная сила раскладывается на три составляющие: окружное, радиальное и осевое усилие (см. рис. 5.1). Силы в зацеплении прямозубой передаче определяются по формулам – окружное усилие
– радиальное усилие
– осевое усилие
где Силы в зацеплении передачи с круговыми зубьями определяются по формулам – окружное усилие
– радиальное усилие
– осевое усилие
где верхний знак – направление вращения (при наблюдении с вершины конуса) и линии наклона зубьев совпадают. При проектировании конических передач с круговыми зубьями необходимо стремиться к тому, чтобы осевая сила При межосевом угле
|
||||||||||||
|
Последнее изменение этой страницы: 2016-08-26; просмотров: 122; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.148.112.15 (0.011 с.) |

 (рис. 4.13). Профиль косого зуба в нормальном сечении
(рис. 4.13). Профиль косого зуба в нормальном сечении  совпадает с профилем прямого зуба. Модуль в этом сечении должен быть стандартным.
совпадает с профилем прямого зуба. Модуль в этом сечении должен быть стандартным. косозубого колеса изменяются в зависимости от угла
косозубого колеса изменяются в зависимости от угла  ;
; ;
; .
. ;
;  ,
, .
. . Радиус кривизны эллипса на малой оси (см. геометрию эллипса) определяется выражением
. Радиус кривизны эллипса на малой оси (см. геометрию эллипса) определяется выражением .
. ;
;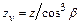 .
.


 (рис. 5.1). Конические передачи сложнее цилиндрических передач в изготовлении и монтаже. Для нарезания зубьев конических зубчатых колес требуются специальные станки и инструмент. При изготовлении зубчатых колес кроме допусков на размеры необходимо выдержать допуски на углы делительных конусов
(рис. 5.1). Конические передачи сложнее цилиндрических передач в изготовлении и монтаже. Для нарезания зубьев конических зубчатых колес требуются специальные станки и инструмент. При изготовлении зубчатых колес кроме допусков на размеры необходимо выдержать допуски на углы делительных конусов  и
и 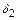 , а также на межосевой угол, а при монтаже конической зубчатой передачи необходимо обеспечить совпадение вершин делительных конусов.
, а также на межосевой угол, а при монтаже конической зубчатой передачи необходимо обеспечить совпадение вершин делительных конусов.


 и составляет с образующей конуса угол
и составляет с образующей конуса угол 

 об/мин,
об/мин,  м/с (допустимо до 8 м/с); более просты в монтаже. При высоких скоростях и значительных нагрузках целесообразнее применять передачи с криволинейными зубьями, поскольку они работают более плавно и бесшумно, имеют большую несущую способность. Из всех колес с непрямыми зубьями на практике получили большее распространение колеса с тангенциальными (косыми) зубьями и колеса с круговыми зубьями.
м/с (допустимо до 8 м/с); более просты в монтаже. При высоких скоростях и значительных нагрузках целесообразнее применять передачи с криволинейными зубьями, поскольку они работают более плавно и бесшумно, имеют большую несущую способность. Из всех колес с непрямыми зубьями на практике получили большее распространение колеса с тангенциальными (косыми) зубьями и колеса с круговыми зубьями. начальные и делительные конусы совпадают.
начальные и делительные конусы совпадают. . По смыслу оно подобно межосевому расстоянию
. По смыслу оно подобно межосевому расстоянию  цилиндрической передачи. Как видно из рис. 5.1 внешние делительные диаметры
цилиндрической передачи. Как видно из рис. 5.1 внешние делительные диаметры  и
и  связаны с внешним конусным расстоянием следующей зависимостью
связаны с внешним конусным расстоянием следующей зависимостью .
. ). Данные размеры обозначаются индексом “
). Данные размеры обозначаются индексом “ 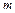 ” и используются и используются при силовых расчетах. Среднее
” и используются и используются при силовых расчетах. Среднее  и внешнее
и внешнее  .
. ,
,  ,
,  ,
, (для колес с прямыми зубьями) и
(для колес с прямыми зубьями) и 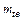 (для колес с круговыми зубьями) – окружные модули на внешнем торце.
(для колес с круговыми зубьями) – окружные модули на внешнем торце.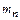 на середине ширины зубчатого венца. Окружной и нормальный модули связаны соотношением
на середине ширины зубчатого венца. Окружной и нормальный модули связаны соотношением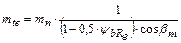 ,
, – коэффициент ширины зубчатого венца (для редукторов со стандартными параметрами рекомендуется принимать
– коэффициент ширины зубчатого венца (для редукторов со стандартными параметрами рекомендуется принимать  );
);  – угол наклона линии зуба.
– угол наклона линии зуба. определяют в зависимости от эквивалентного числа зубьев
определяют в зависимости от эквивалентного числа зубьев 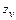 и передаточного числа
и передаточного числа  по таблицам, приведенным в ГОСТ 19624-74 и ГОСТ 19326-73, или по формуле ЭНИМС
по таблицам, приведенным в ГОСТ 19624-74 и ГОСТ 19326-73, или по формуле ЭНИМС ,
, – для прямозубой передачи;
– для прямозубой передачи; 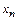 – для передачи с круговыми зубьями.
– для передачи с круговыми зубьями.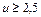 рекомендуется применять тангенциальную коррекцию, заключающуюся в утолщении зуба шестерни и соответствующем утончении зуба колеса.
рекомендуется применять тангенциальную коррекцию, заключающуюся в утолщении зуба шестерни и соответствующем утончении зуба колеса. .
.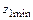 выбирается в зависимости от угла
выбирается в зависимости от угла  и
и  были кратны друг другу или имели, возможно, большее число общих делителей.
были кратны друг другу или имели, возможно, большее число общих делителей. передаточное число определяется по формуле
передаточное число определяется по формуле . (5.1)
. (5.1) определяется по аналогии с цилиндрическими косозубыми передачами по формуле
определяется по аналогии с цилиндрическими косозубыми передачами по формуле .
. . Для конических зубчатых колес с тангенциальным зубом (косым) зубом
. Для конических зубчатых колес с тангенциальным зубом (косым) зубом 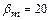 …
…  . Угол
. Угол  .
. .
. .
. и
и  …100,
…100,  .
.


 , а также для колес с тангенциальными зубьями,
, а также для колес с тангенциальными зубьями,  .
. ,
,  и среднем конусном расстоянии
и среднем конусном расстоянии  .
. ;
;  ;
; ;
; ,
, – угол профиля.
– угол профиля. ;
; ,
, была направлена к основанию конуса шестерни. Для этого при ведущей шестерне направление вращения и направление линии зуба должны совпадать. При ведомой шестерне эти направления должны быть противоположными. Направление осевой силы к вершине конуса нежелательно в связи с возможностью заклинивания передачи при значительных осевых зазорах в подшипниках.
была направлена к основанию конуса шестерни. Для этого при ведущей шестерне направление вращения и направление линии зуба должны совпадать. При ведомой шестерне эти направления должны быть противоположными. Направление осевой силы к вершине конуса нежелательно в связи с возможностью заклинивания передачи при значительных осевых зазорах в подшипниках. ,
,  .
.


