
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Кинематические характеристики цилиндрическихСодержание книги
Поиск на нашем сайте
Кинематические характеристики цилиндрических Модификация профилей зубьев Модификация профилей зубьев увеличивает преимущества эвольвентного зацепления, обеспечивая уменьшение минимально допустимых чисел зубьев, повышение изгибной и контактной прочности, повышение износостойкости и стойкости против заедания, повышение плавности работы. Модификация применяется в основном для прямозубых передач. Для косозубых передач она в основном используется для вписывания в стандартное межосевое расстояние и при малых числах зубьев шестерни. При положительном смещении исходного контура обеспечивается: – повышение изгибной прочности зубьев за счет утолщения зуба у основания; – возможность уменьшения числа зубьев и увеличения модуля зацепления при том же начальном диаметре шестерни (повышается изгибная прочность); – повышение контактной прочности зубьев за счет увеличения радиусов кривизны профилей зубьев шестерни Однако улучшение одних параметров с повышением коэффициентов смещения, например, прочности, обычно связано с ухудшением других параметров, например, плавности работы (снижается коэффициент перекрытия Модификация смещением исходного контура может быть высотной и угловой. При высотной модификации суммарный коэффициент смещения равен нулю При угловой модификации суммарный коэффициент отличен от нуля Для передач, несущая способность которых определяется контактной выносливостью, необходимо возможно большее увеличение приведенного радиуса кривизны, что обеспечивается выбором максимально возможного суммарного коэффициента смещения; при этом также повышается изгибная прочность передачи. Для передач, несущая способность которых определяется прочностью зубьев на изгиб, модификация должна обеспечить повышение прочности и равнопрочность по изгибу зубьев шестерни и колеса. Для передач, несущая способность которых ограничивается заеданием или механическим изнашиванием, модификация должна уменьшать и выравнивать скорости относительного скольжения в крайних точках зацепления; для повышения износостойкости целесообразно также уменьшать высоту ножки зуба шестерни. Предельные значения коэффициентов смещения ограничиваются следующими факторами: – подрезанием зубьев у основания; – заострением зубьев у вершины; толщина зуба у вершины – интерференцией профилей зубьев при работе; – коэффициентом перекрытия; для прямозубых передач Наиболее универсальным методом определения коэффициентов смещения является метод блокирующих контуров, устанавливающий область допустимых значений коэффициентов смещения шестерни
Рис. 4.5. Блокирующий контур: 1 – граница подрезания зуба шестерни; 2 – граница подрезания зуба колеса; 3, 4 – граница интерференции профилей зубьев; 5 – зона не рекомендуемых значений
Коэффициенты смещения
Рис. 4.6.
Точность изготовления зубчатых передач задается степенью точности и требованием к боковому зазору – видом сопряжения по нормам бокового зазора. Вид сопряжения определяет гарантированный боковой зазор
Таблица 4.1
Вид сопряжения определяют независимо от степени точности передачи по расчетному значению бокового зазора:
где Боковой зазор, необходимый для компенсации температурных деформаций деталей, определяется по формуле
где Боковой зазор
где 10 – для тихоходных передач; 30 – для быстроходных передач; Вид сопряжения назначают исходя из следующего условия:
Если для расчета недостаточно исходных данных, то обычно для силовых передач рекомендуется к использованию сопряжение В. Данное сопряжение гарантирует минимальное значение бокового зазора Примеры обозначения точности зубчатых передач: а) точность передачи со степенью точности 7 по всем трем нормам (кинематической точности, плавности работы, контакта зубьев) с видом сопряжения колес С и соответствием между видом сопряжения и допуском на боковой зазор обозначается следующим образом 7-С ГОСТ1643-81. б) при комбинировании норм разных степеней точности и изменении соответствия между видом сопряжения и допуском на боковой зазор точность зубчатых колес и передач обозначается последовательным написанием трех цифр и двух букв 8-7-6-Ва ГОСТ1643-81. Показателями, обеспечивающими гарантированный боковой зазор, являются: – для зубчатых колес наименьшее отклонение длины общей нормали – для передач с нерегулируемым расположением осей отклонение межосевого расстояния – для передач с регулируемым расположением осей
Поломка зубьев Поломка зубьев связана с действием напряжений изгиба. Различают следующие виды поломки зубьев: – поломка от перегрузок ударного или статического характера; предупреждают защитой привода от перегрузок или учетом перегрузок при расчете; – усталостная поломка под действием переменных напряжений в течение длительного срока службы. В последнем случае особое значение имеют меры по устранению концентраторов напряжений: – рисок от механической обработки; – раковин и трещин в отливках; – микротрещин от термообработки и т.п. Меры предупреждения поломки зубьев: – увеличение модуля зацепления (возрастает площадь опасного сечения у основания зуба); – положительное смещение при нарезании зубьев (возрастает площадь опасного сечения у основания зуба); – увеличение твердости за счет термообработки; – увеличение механических характеристик материала зубчатых колес за счет наклепа (механического упрочнения материала), повышающего упругие свойства материала в результате предварительного пластического деформирования (рис. 4.9); – уменьшение концентрации нагрузки по краям зубьев: жесткие валы, зубья со срезанными углами (рис. 4.10, а), зубья бочкообразной формы (рис. 4.10, б).
Рис. 4.9. Диаграмма растяжения
Рис. 4.10
Материал и термообработка
Нагрузка, допускаемая по контактной прочности зубьев, определяется в основном твердостью материала. Наибольшую твердость, а, следовательно, наименьшие габариты и массу передачи можно получить при изготовлении зубчатых колес из сталей, подвергнутых термообработке. Некоторые из сталей, рекомендуемых для зубчатых колес, виды их термообработки и механические характеристики приведены в табл. 4.2. В зависимости от твердости материалы зубчатых колес условно делятся на две основные группы: – с твердостью – с твердостью НВ > 350 (термообработка: объемная закалка, поверхностная закалка ТВЧ, цементация, азотирование и т.д.). Таблица 4.2. Механические характеристики сталей
Твердость материала
Технологические преимущества материала при При НВ > 350 твердость материала обычно выражается в единицах Роквелла (HRC). Специальные виды термообработки позволяют получить твердость материала до 50…60 HRC (до 500…650 НВ). При этом допускаемые контактные напряжения увеличиваются до двух раз, а нагрузочная способность передачи до четырех раз по сравнению с нормализованными или улучшенными сталями. Возрастает также износостойкость и стойкость против заедания. Применение высокотвердых материалов является большим резервом повышения нагрузочной способности зубчатых передач, но с высокой твердостью связаны дополнительные трудности: – высокотвердые материалы плохо прирабатываются, поэтому требуется повышенная точность изготовления передачи, повышенная жесткость валов и опор; – нарезание зубьев при высокой твердости затруднено, поэтому термообработка проводится после нарезания зубьев; некоторые виды термообработки (объемная закалка, цементация) сопровождаются значительным короблением зубьев; для исправления формы зубьев требуются дополнительные операции (шлифовка, притирка, обкатка и т.п.); данные трудности проще преодолеть в условиях крупносерийного и массового производства, когда окупаются затраты на специальное оборудование, приспособления и инструменты.
Допускаемые напряжения
Решение. 1. Срок службы привода Определяем срок службы привода в часах по формуле:
2. Выбор материала зубчатых колес В качестве материала зубчатых колес по табл. 4.2 выбираем сталь 40ХН, термообработка У+ТВЧ. Механические характеристики материала заносим в табл. 4.9.
Таблица 4.9. Механические характеристики сталей
3. Расчет допускаемых контактных напряжений По формуле, приведенной в табл. 4.3, определяем предел контактной выносливости материала шестерни и колеса, МПа:
Для колес с поверхностным упрочнением зубьев (поверхностная закалка ТВЧ, цементация, азотирование) Для постоянного режима нагружения эквивалентное число циклов перемен напряжений материалов шестерни и колеса определяем по формуле
По табл. 4.4 в зависимости от средней твердости методом линейной интерполяции определяем базовое число циклов перемен напряжений материалов шестерни и колеса. Из рис. 4.11. имеем
Рис. 4.11. К определению базового числа циклов перемен напряжений
Поскольку Определяем допускаемое контактное напряжение, МПа:
4. Проектный расчет на контактную выносливость. Определение основных геометрических параметров передачи По табл. 4.5 назначаем коэффициент ширины колеса по межосевому расстоянию:
По табл. 4.6 в зависимости от расположения колеса относительно опор (по условию задачи – несимметричное, см. рис. 2.5) выбираем коэффициент, учитывающий неравномерность распределения нагрузки по ширине зубчатого венца
Определяем по формуле 4.14 межосевое расстояние, мм:
Принимаем по табл. 4.7 Определяем модуль зацепления, мм, по следующей рекомендации:
Из полученного интервала модулей выбирается стандартное значение (табл. 4.8):
Определяем ширину зубчатого венца колеса, мм:
Принимаем из ряда нормальных линейных размеров (ГОСТ 6636-69) ширину зубчатого венца колеса Определяем минимальный угол наклона зубьев, град.:
Определяем суммарное число зубьев:
Принимаем Уточняем угол наклона зубьев по формуле (4.8), град.:
Определяем по формулам (4.10) число зубьев шестерни и колеса:
Уточняем передаточное число:
Определяем по формулам (4.6) делительные диаметры, мм:
По формуле (4.1) проверяем межосевое расстояние:
Определяем диаметры вершин и впадин зубьев, мм:
Силы в зацеплении В общем случае (косозубая цилиндрическая передача) нормальная сила в зацеплении – окружное усилие
– радиальное усилие
– осевое усилие (для прямозубых передач равно нулю)
Рис. 4.12. Силы в зацеплении цилиндрической передачи
Рис. 4.13
Эквивалентные параметры используются для распространения расчетов на прочность цилиндрических прямозубых передач на цилиндрические косозубые передачи. Увеличение эквивалентных параметров с увеличением угла
Общие сведения Конические зубчатые передачи относятся к зубчатым передачам с пересекающимися осями. Наиболее распространены передачи с углом пересечения осей колес (межосевым углом) Пересечение осей валов конических зубчатых колес затрудняет размещение опор. Поэтому одно из конических колес, как правило, шестерню размещают консольно по отношению к опорам. Это приводит к увеличению неравномерности распределения нагрузки по ширине зубчатого венца. В конических передачах действуют значительные осевые силы, что приводит к усложнению конструкции опор. Перечисленное выше приводит к тому, что нагрузочная способность конической прямозубой передачи составляет 85 % от нагрузочной способности цилиндрической прямозубой передачи. Конические зубчатые колеса подразделяются на колеса с прямыми и непрямыми зубьями. Основными типами колес с непрямыми зубьями являются следующие конические зубчатые колеса:
Рис. 5.1
а) колеса с тангенциальными зубьями; тангенциальный зуб направлен по касательной к некоторой воображаемой окружности радиусом
Рис. 5.2
б) колеса с эвольвентной линией зуба (продольная кривизна зуба выполнена по удлиненной эвольвенте); в) колеса с эвольвентной линией зуба (продольная кривизна зуба выполнена по удлиненной эвольвенте); г) колеса с круговыми зубьями (продольная кривизна зуба выполнена по дуге окружности); б) колеса с шевронными зубьями. Прямозубые передачи обычно применяются при небольших нагрузках и невысоких скоростях: Геометрические параметры Аналогами начальных и делительных цилиндров цилиндрических передач являются начальные и делительные конусы с углами Важнейшим геометрическим параметром конической передачи является внешнее конусное расстояние
Кроме размеров по внешнему торцу конуса, удобных для измерения и указываемых на чертежах, различают также размеры в среднем сечении (по средине зубчатого венца
Ширину зубчатого венца рекомендуется выбирать исходя из следующих условий
где Кроме окружного модуля различают также нормальный модуль
где Круговые зубья нарезают немодульным инструментом, позволяющим нарезать зубья в некотором диапазоне модулей. Поэтому в данном случае допускается применять передачи с нестандартными и дробными модулями. Для конических зубчатых передач главным образом применяется высотная коррекция для выравнивания удельных скольжений в зацеплении. Коэффициенты смещения
где Для конических передач при Как правило, для конических зубчатых передач применяют высотную коррекцию в сочетании с тангенциальной коррекцией. Применение высотной коррекции повышает износостойкость и сопротивление зубьев заеданию, тангенциальная коррекция выравнивает прочность зубьев.
Кинематические параметры Передаточное число конической зубчатой передачи определяется по формулам
Минимальное число зубьев шестерни Для уменьшения шума рекомендуется применять притирку и выбирать некратные числа зубьев колес. Если передача работает при постоянной нагрузке и умеренных линейных скоростях, то необходимо стремиться к тому, чтобы числа зубьев колес При межосевом угле
Зависимость (5.1) обычно используется для определения углов делительных конусов. Коэффициент осевого перекрытия
Для конических колес с круговым зубом предпочтителен к применению угол Угол наклона линии зуба может быть определен также по формуле
Угол
Осевая форма зуба ГОСТ 19326-73 регламентирует три основные формы конусности (изменение размеров сечений по длине зуба). При осевой форме зуба I (рис. 5.3, а) вершины делительного конуса и конуса впадин зубьев совпадают. Благодаря этому обеспечивается постоянство радиального зазора по всей длине зуба. Это позволяет увеличить радиус закругления у основания зуба и повысить его изгибную прочность. Данную форму конусности применяют для конических передач с прямыми и тангенциальными зубьями, а также для колес с круговыми зубьями при
Рис. 5.3
При осевой форме зуба II (рис. 5.3, б) вершины делительного конуса и конуса впадин зубьев не совпадают. Это обеспечивает одинаковую ширину впадины по длине зуба. При этом толщина зуба по делительному конусу растет с увеличением расстояния от вершины. Данную форму конусности применяют для конических передач с круговыми зубьями при При осевой форме зуба III (рис. 5.3, в) образующие делительного конуса, конусов вершин и впадин зубьев параллельны (равновысокие зубья, т.е. зубья не имеют конусности по высоте). Данную форму конусности применяют для конических передач с круговыми зубьями при В зубчатых колесах с зубьями формы конусности I обычно оперируют окружным модулем Силы в зацеплении Также как и в косозубой цилиндрической передаче в конической зубчатой передаче нормальная сила раскладывается на три составляющие: окружное, радиальное и осевое усилие (см. рис. 5.1). Силы в зацеплении прямозубой передаче определяются по формулам – окружное усилие
– радиальное усилие
– осевое усилие
где Силы в зацеплении передачи с круговыми зубьями определяются по формулам – окружное усилие
– радиальное усилие
– осевое усилие
где верхний знак – направление вращения (при наблюдении с вершины конуса) и линии наклона зубьев совпадают. При проектировании конических передач с круговыми зубьями необходимо стремиться к тому, чтобы осевая сила При межосевом угле
На контактную выносливос |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-08-26; просмотров: 93; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.21.46.68 (0.014 с.) |

 и колеса
и колеса  и соответствующего уменьшения удельного давления (
и соответствующего уменьшения удельного давления (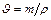 – коэффициент удельного давления;
– коэффициент удельного давления;  – приведенный радиус кривизны).
– приведенный радиус кривизны). ).
).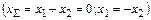 . В данном случае шестерня упрочняется по изгибу за счет колеса. Эта модификация применяется при малых числах зубьев шестерни
. В данном случае шестерня упрочняется по изгибу за счет колеса. Эта модификация применяется при малых числах зубьев шестерни  и больших передаточных числах
и больших передаточных числах  . При использовании данной модификации не изменяется межосевое расстояние, начальные и делительные окружности совпадают
. При использовании данной модификации не изменяется межосевое расстояние, начальные и делительные окружности совпадают  . Зацепление в данном случае называется равносмещенным.
. Зацепление в данном случае называется равносмещенным.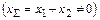 . При
. При 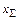 > 0 зацепление называется положительным, а при
> 0 зацепление называется положительным, а при  , для прямозубых передач минимальное число зубьев
, для прямозубых передач минимальное число зубьев  , для косозубых передач
, для косозубых передач  ;
; ;
; .
. и колеса
и колеса  . Блокирующий контур (рис. 4.5) строится в координатах
. Блокирующий контур (рис. 4.5) строится в координатах  и
и  .
.
 – коэффициент скольжения
– коэффициент скольжения между неработающими профилями зубьев, измеренный по общей нормали к эвольвентным профилям зубьев. Боковой зазор назначают с учетом обеспечения смазывания зубьев, необходимости компенсации погрешностей изготовления и температурных деформаций.
между неработающими профилями зубьев, измеренный по общей нормали к эвольвентным профилям зубьев. Боковой зазор назначают с учетом обеспечения смазывания зубьев, необходимости компенсации погрешностей изготовления и температурных деформаций.
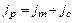 ,
, – расчетный боковой зазор, мкм;
– расчетный боковой зазор, мкм;  – боковой зазор, необходимый для компенсации температурных деформаций деталей, мкм;
– боковой зазор, необходимый для компенсации температурных деформаций деталей, мкм;  – боковой зазор, необходимый для размещения слоя смазочного материала, мкм.
– боковой зазор, необходимый для размещения слоя смазочного материала, мкм. ,
, – коэффициент температурного расширения материала зубчатых колес;
– коэффициент температурного расширения материала зубчатых колес; 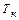 – температура нагрева зубчатых колес;
– температура нагрева зубчатых колес;  – коэффициент температурного расширения материала корпусных деталей;
– коэффициент температурного расширения материала корпусных деталей; 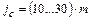 ,
,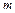 – модуль зацепления, мм.
– модуль зацепления, мм. .
. , при котором исключается возможность заклинивание стальной или чугунной передачи от нагрева при разности температур колеса и корпуса
, при котором исключается возможность заклинивание стальной или чугунной передачи от нагрева при разности температур колеса и корпуса  °С. Сопряжение Н применяют в реверсивных тихоходных передачах с жесткими требованиями в отношении мертвого хода. При этом если передача предназначена для работы в условиях значительного колебания температур, зубчатые колеса и корпус должны быть изготовлены из материалов с одинаковыми коэффициентами линейного расширения
°С. Сопряжение Н применяют в реверсивных тихоходных передачах с жесткими требованиями в отношении мертвого хода. При этом если передача предназначена для работы в условиях значительного колебания температур, зубчатые колеса и корпус должны быть изготовлены из материалов с одинаковыми коэффициентами линейного расширения  . При m < 1 рекомендуется к использованию сопряжение F.
. При m < 1 рекомендуется к использованию сопряжение F.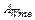 или наименьшее отклонение толщины зуба по постоянной хорде
или наименьшее отклонение толщины зуба по постоянной хорде  (контролируются при изготовлении зубчатых колес);
(контролируются при изготовлении зубчатых колес); (контролируется при сборке передачи);
(контролируется при сборке передачи);

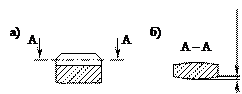
 (термообработка: нормализация или улучшение);
(термообработка: нормализация или улучшение); ,
мм
,
мм
 ,
мм
,
мм
 .
. ;
; .
.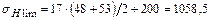 .
. . Принимаем
. Принимаем  .
. ;
; ;
;  .
.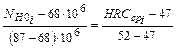 ;
;  ;
; .
.
 <
<  и
и  <
<  коэффициенты долговечности принимаем равными
коэффициенты долговечности принимаем равными  .
. ;
;  ;.
;.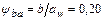 .
. .
. .
. мм.
мм. ;
;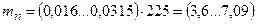 .
. .
. ;
;  .
. мм.
мм.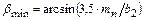 ;
;  .
. ;
;  .
.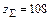 .
. ;
;  .
. ;
;  .
. ;
;  %;
%; ;
;  %.
%. ;
; 
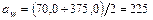 .
. ;
;  ;
;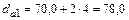 ;
;  ;
; ;
;  .
. раскладывается на три составляющие (рис. 4.12):
раскладывается на три составляющие (рис. 4.12): ;
; ;
;  ;
; .
.
 является одной из причин повышения прочности косозубых передач. Вследствие наклона зубьев получается колесо как бы больших размеров или при той же нагрузке уменьшаются габариты передачи.
является одной из причин повышения прочности косозубых передач. Вследствие наклона зубьев получается колесо как бы больших размеров или при той же нагрузке уменьшаются габариты передачи. (рис. 5.1). Конические передачи сложнее цилиндрических передач в изготовлении и монтаже. Для нарезания зубьев конических зубчатых колес требуются специальные станки и инструмент. При изготовлении зубчатых колес кроме допусков на размеры необходимо выдержать допуски на углы делительных конусов
(рис. 5.1). Конические передачи сложнее цилиндрических передач в изготовлении и монтаже. Для нарезания зубьев конических зубчатых колес требуются специальные станки и инструмент. При изготовлении зубчатых колес кроме допусков на размеры необходимо выдержать допуски на углы делительных конусов  и
и 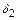 , а также на межосевой угол, а при монтаже конической зубчатой передачи необходимо обеспечить совпадение вершин делительных конусов.
, а также на межосевой угол, а при монтаже конической зубчатой передачи необходимо обеспечить совпадение вершин делительных конусов.


 и составляет с образующей конуса угол
и составляет с образующей конуса угол 

 об/мин,
об/мин,  м/с (допустимо до 8 м/с); более просты в монтаже. При высоких скоростях и значительных нагрузках целесообразнее применять передачи с криволинейными зубьями, поскольку они работают более плавно и бесшумно, имеют большую несущую способность. Из всех колес с непрямыми зубьями на практике получили большее распространение колеса с тангенциальными (косыми) зубьями и колеса с круговыми зубьями.
м/с (допустимо до 8 м/с); более просты в монтаже. При высоких скоростях и значительных нагрузках целесообразнее применять передачи с криволинейными зубьями, поскольку они работают более плавно и бесшумно, имеют большую несущую способность. Из всех колес с непрямыми зубьями на практике получили большее распространение колеса с тангенциальными (косыми) зубьями и колеса с круговыми зубьями. начальные и делительные конусы совпадают.
начальные и делительные конусы совпадают. . По смыслу оно подобно межосевому расстоянию
. По смыслу оно подобно межосевому расстоянию  цилиндрической передачи. Как видно из рис. 5.1 внешние делительные диаметры
цилиндрической передачи. Как видно из рис. 5.1 внешние делительные диаметры  и
и  связаны с внешним конусным расстоянием следующей зависимостью
связаны с внешним конусным расстоянием следующей зависимостью .
. ). Данные размеры обозначаются индексом “
). Данные размеры обозначаются индексом “  и внешнее
и внешнее  .
. ,
,  ,
,  ,
, (для колес с прямыми зубьями) и
(для колес с прямыми зубьями) и 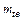 (для колес с круговыми зубьями) – окружные модули на внешнем торце.
(для колес с круговыми зубьями) – окружные модули на внешнем торце.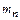 на середине ширины зубчатого венца. Окружной и нормальный модули связаны соотношением
на середине ширины зубчатого венца. Окружной и нормальный модули связаны соотношением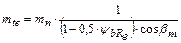 ,
, – коэффициент ширины зубчатого венца (для редукторов со стандартными параметрами рекомендуется принимать
– коэффициент ширины зубчатого венца (для редукторов со стандартными параметрами рекомендуется принимать  );
);  – угол наклона линии зуба.
– угол наклона линии зуба. определяют в зависимости от эквивалентного числа зубьев
определяют в зависимости от эквивалентного числа зубьев 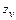 и передаточного числа
и передаточного числа  по таблицам, приведенным в ГОСТ 19624-74 и ГОСТ 19326-73, или по формуле ЭНИМС
по таблицам, приведенным в ГОСТ 19624-74 и ГОСТ 19326-73, или по формуле ЭНИМС ,
, – для прямозубой передачи;
– для прямозубой передачи; 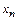 – для передачи с круговыми зубьями.
– для передачи с круговыми зубьями.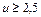 рекомендуется применять тангенциальную коррекцию, заключающуюся в утолщении зуба шестерни и соответствующем утончении зуба колеса.
рекомендуется применять тангенциальную коррекцию, заключающуюся в утолщении зуба шестерни и соответствующем утончении зуба колеса. .
.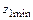 выбирается в зависимости от угла
выбирается в зависимости от угла  передаточное число определяется по формуле
передаточное число определяется по формуле . (5.1)
. (5.1) определяется по аналогии с цилиндрическими косозубыми передачами по формуле
определяется по аналогии с цилиндрическими косозубыми передачами по формуле .
. . Для конических зубчатых колес с тангенциальным зубом (косым) зубом
. Для конических зубчатых колес с тангенциальным зубом (косым) зубом 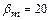 …
…  . Угол
. Угол  .
. .
. .
. и
и  …100,
…100,  .
.


 , а также для колес с тангенциальными зубьями,
, а также для колес с тангенциальными зубьями,  .
. ,
,  и среднем конусном расстоянии
и среднем конусном расстоянии  .
. ;
;  ;
; ,
, – угол профиля.
– угол профиля. ;
; ,
, была направлена к основанию конуса шестерни. Для этого при ведущей шестерне направление вращения и направление линии зуба должны совпадать. При ведомой шестерне эти направления должны быть противоположными. Направление осевой силы к вершине конуса нежелательно в связи с возможностью заклинивания передачи при значительных осевых зазорах в подшипниках.
была направлена к основанию конуса шестерни. Для этого при ведущей шестерне направление вращения и направление линии зуба должны совпадать. При ведомой шестерне эти направления должны быть противоположными. Направление осевой силы к вершине конуса нежелательно в связи с возможностью заклинивания передачи при значительных осевых зазорах в подшипниках. ,
,  .
.


