
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Расчет допускаемых напряжений для проектирования цилиндрических и конических зубчатых передачСодержание книги
Поиск на нашем сайте
Выбор материала и термообработки Таблица 2.1 Механические характеристики сталей, используемых для изготовления зубчатых колес
Таблица 2.2 Предел контактной выносливости при базовом числе циклов
Практикой эксплуатации и специальными исследованиями установлено, что нагрузка, допускаемая по контактной прочности зубьев, определяется в основном твердостью материала. Высокую твердость в сочетании с другими характеристиками, а, следовательно, малые габариты и массу передачи можно получить при изготовлении зубчатых колес из сталей, подвергнутых термообработке. Сталь в настоящее время — основной материал для изготовления зубчатых колес. В зависимости от твердости (или термообработки) стальные зубчатые колеса разделяют на две основные группы: твердостью H ≤ 350 НВ — зубчатые колеса, нормализованные или улучшенные; твердостью Н> 350 НВ — с объемной закалкой, закалкой ТВЧ, цементацией, азотированием и др. Эти группы различны по технологии, нагрузочной способности и способности к приработке. Твердость материала менее 350 НВ позволяет производить чистовое нарезание зубьев после термообработки. При этом можно получать высокую точность без применения дорогих отделочных операций (шлифовки, притирки и т. п.). Колеса этой группы хорошо прирабатываются и не подвержены хрупкому разрушению при динамических нагрузках. Для лучшей приработки зубьев твердость прямозубой шестерни рекомендуют назначать больше твердости колеса не менее чем на (10...15) единиц Н1=Н2 + (10...15)НВ косозубой шестерни – на (50…70) единиц Н1=Н2 + (50...70)НВ Технологические преимущества материала при Н<350 НВ обеспечили ему широкое распространение в условиях индивидуального и мелкосерийного производства, в мало- и средненагруженных передачах, а также в передачах с большими колесами, термическая обработка которых затруднена. При Н>350 НВ (вторая группа материалов) твердость выражается обычно в единицах Роквелла — НRС Специальные виды термообработки позволяют получить твердость Н = (50...60) НRС. При этом допускаемые контактные напряжения увеличиваются до двух раз, а нагрузочная способность передачи — до четырех раз по сравнению с нормализованными или улучшенными сталями. Возрастают также износостойкость и стойкость против заедания. Применение высокотвердых материалов является большим резервом повышения нагрузочной способности зубчатых передач. Однако с высокой твердостью связаны некоторые дополнительные трудности: 1.Высокотвердые материалы плохо прирабатываются, 2.Нарезание зубьев при высокой твердости затруднено, поэтому термообработку выполняют после нарезания. 3.Эти трудности проще преодолеть в условиях крупносерийного и массового производства, когда окупаются затраты на специальное оборудование. Расчёт допускаемых напряжений для входной косозубой ступени Допускаемые контактные напряжения при расчёте на усталость Выбираем для входной ступени материал – сталь 45 с твёрдостью для шестерни HB 260 (улучшение) и для колеса HB 210 (нормализация). Выписываем из таблицы 1 механические характеристики стали для шестерни и колеса
Определяем допускаемые контактные напряжения
где
где
Для твёрдости колёс HB<350
Коэффициент запаса прочности принимаем
Определяем срок службы передачи в часах
Так как режим нагрузки переменный, то определяем эквивалентное число циклов нагружения
где
Для нашего случая, когда частота постоянна
или
Число циклов нагружения колеса будет в
Определяем базовое число циклов
При условии, что
Для расчёта определяем
Проверяем отношение
Окончательно, для расчёта первой ступени принимаем
Расчёт допускаемых напряжений для выходной прямозубой ступени Допускаемые контактные напряжения при расчёте на усталость Выбираем для выходной ступени материал – сталь 45 с твёрдостью для шестерни HB 260 (улучшение) и для колеса HB 245 (нормализация). Выписываем из таблицы 1 механические характеристики стали для шестерни и колеса
Базовое число циклов Эквивалентное число циклов нагружения для шестерни будет равным числу циклов для колеса первой ступени, так как они установлены на одном валу
Для колеса
Тогда
Таким образом, для расчёта второй ступени допускаемое напряжение получаем
Проверяем отношение
Условие выполняется
Допускаемые напряжения изгиба при расчете на усталость
где
При термообработке –улучшение Входная косозубая ступень
где
где Для нормализованных и улучшенных сталей
Так как
Выходная прямозубая ступень
где
где Для нормализованных и улучшенных сталей
Так как
Допускаемые напряжения для проверки прочности зубьев при перегрузках Напряжения одинаковы для обеих ступеней
Допускаемые напряжения для проверки прочности зубьев при перегрузках Напряжения одинаковы для обеих ступеней
3 Проектирование косозубых цилиндрических передач 1 Разрушения активных поверхностей зубьев в результате развития усталостного выкрашивания и поломки их являются основными причинами выхода из строя зубчатых колес. Расчет на усталостную выносливость проводится с целью предотвращения преждевременного выхода их из строя. На первом этапе расчета (проектный расчет) преследуют цель предварительного определения размеров колес и передач на основе контактной прочности рабочих поверхностей зубьев. Далее размеры колес и передачи уточняют, проверяя на выносливость зубья по контактным и изгибным напряжениям. При необходимости проверяют прочность зубьев при перегрузках. При расчете косозубой цилиндрической передачи закрытого типа для редуктора общего назначения ряд параметров (межосевое расстояние, модуль) должен соответствовать действующим стандартам, величины других должны находиться в рекомендуемых пределах. Эти требования могут быть легко реализованы при расчете на ЭВМ. 2 Исходные данные для расчета 2.1 T1 - крутящий момент на валу шестерни, Н*м; 2.2 [ σH] - допускаемые контактные напряжения, МПа; 2.3 [σF]1 - допускаемые напряжения изгиба для шестерни, МПа; 2.4 [σF]2 - допускаемые напряжения изгиба для колеса, МПа; 2.5 [σH]max - допускаемые контактные напряжения при перегрузке, МПа; 2.6 [σF]max - допускаемые напряжения изгиба при перегрузке, МПа; 2.7 U - передаточное число; 2.8 КHβ - коэффициент неравномерности распределения нагрузки по ширине зуба при расчете по контактным напряжениям; 2.9 КFβ - коэффициент неравномерности распределения нагрузки по ширине зуба при расчете по напряжениям изгиба; 2.10 ψbd - коэффициент ширины шестерни относительно делительного диаметра; 2.11 ψbа - коэффициент ширины шестерни относительно межосевого расстояния;
2.12 β - угол наклона зуба. Выбирается в пределах от 8° до 15°. Для шевронных передач - до 25°. 2.13 αω - угол зацепления. Для передач без смещения αω=20°. 2.14 n1 - частота вращения вала шестерни, об/мин. 3. Алгоритм расчета косозубой цилиндрической передачи 3.1 Межосевое расстояние
Расчетное значение аW для нестандартных редукторов округлить по ряду Rа 40:...80,85,90,95,100,105,110,120,125,130 далее через 10 до 200 и через 20 до 420. 3.2 Модуль
Величину mn согласовать со стандартом СЭВ З10-76 1 ряд: 1.5; 2.0; 2.5; 3; 4; 5 2 ряд: 1.75; 2.25; 2.75; 3.5; 4.5; 5.5. Первый ряд следует предпочитать второму. 3.3 Суммарное число зубьев передачи
Величину 3.4 Число зубьев шестерни.
Полученное значение z1 округлить до целого числа. 3,5 Число зубьев колеса
3.6 Уточним величину угла наклона зуба
3.7 Делительные диаметры шестерни и колеса
3.8 Уточним межосевое расстояние
.9 Уточним передаточное число
3.10 Рабочая ширина зубчатого венца
3.11 Эквивалентные числа зубьев шестерни и колеса
3.12 Окружная скорость в передаче
3.13 Коэффициент торцового перекрытия
3.14 Выбрать по рекомендациям коэффициенты динамической нагрузки
3.15 Коэффициент осевого перекрытия
3.16 Определим величину коэффициента Zε, учитывающего суммарную длину контактных линий
Если Если 3.17 Определим величину коэффициента ZH, учитывающего форму сопряженных поверхностей зубьев
3.18 Удельная расчетная окружная сила при расчете по контактным напряжениям
3.19 Вычислим величину рабочих контактных напряжений
3.20 Проверим выполнение условий
Если не выполняется первое условие, то необходимо увеличить значение bW в выражении для ωHt (п. 3.18.), если не выполняется второе условие, необходимо bW - уменьшить. 3.21 Проверим передачу по максимальным контактным напряжениям при перегрузке
3.22 Удельная расчетная окружная сила при расчете по напряжениям изгиба
3.23 Вспомогательный коэффициент Kε
3.24 Коэффициент Yε, учитывающий перекрытие зубьев
3.25 Коэффициент Yβ, учитывающий наклон зуба
3.26 Вычислим
где yF1, уF2 - коэффициент формы зуба для шестерни и колеса. Если условие выполняется, то
Если условие не выполняется, то
3.27 Проверим передачу по максимальным напряжениям изгиба при перегрузке
3.28 Геометрия передачи: 3.28.1 Диаметры окружностей выступов зубьев шестерни и колеса
3.28.2 Диаметры окружностей впадин зубьев и колеса
3.29 Усилия в зацеплении 3.29.1 Окружная сила
3.29.2 Осевая сила
3.29.3 Радиальная сила
4 Проектирование прямозубых цилиндрических передач
1 Размеры закрытой прямозубой зубчатой передачи редукторного типа в большинстве случаев определяют из расчета рабочих поверхностей зубьев на выносливость по контактным напряжениям (расчет на отсутствие усталостного выкрашивания). Величина модуля согласуется со стандартом СТ СЭВ 310-76. Проверочный расчет передачи на выносливость по контактным напряжениям проводится для уточнения ее размеров и величины реально действующих в передаче контактных напряжений на основе полученных ее размеров. Также проводят проверочный расчет зубьев на выносливость по напряжениям изгиба. В большинстве случаев напряжения изгиба в зубьях колес, рассчитанных на контактную прочность, весьма невелики. Для передач, работающих со значительными перегрузками, проверяют контактные напряжения и напряжения изгиба при максимальной нагрузке. Проектирование передачи ведётся по программе с использованием табличного редактора MICROSOFT EXCEL. Программа обеспечивает расчёт передачи в диалоговом режиме, простоту и наглядность, многовариантность и оптимизацию размеров.
2. Исходные данные для расчета
2.1 T1 - крутящий момент на валу шестерни, Н*м; 2.2 [σH] - допускаемые контактные напряжения, МПа; 2.3 [σF]1 - допускаемые напряжения изгиба для шестерни, МПа; 2.4 [σF]2 - допускаемые напряжения изгиба для колеса, МПа; 2.5 [σH]max- допускаемые контактные напряжения при перегрузке, МПа; 2.6 [σF]max - допускаемые напряжения изгиба при перегрузке, МПа; 2.7 u - передаточное число; 2.8 КHβ - коэффициент неравномерности распределения нагрузки по ширине зуба при расчете по контактным напряжениям; 2.9 КFβ - коэффициент неравномерности распределения нагрузки по ширине зуба при расчете по напряжениям изгиба; 2.10 ψbd- коэффициент ширины шестерни относительно делительного диаметра; 2.11 αω - угол зацепления. Для передач без смещения αω=20°. 2.12 n1 - частота вращения вала шестерни, об/мин. 2.13
2.14 2.15
3 Алгоритм расчета прямозубой цилиндрической передачи
3.1 Определяем делительный диаметр шестерни
3.2 Рабочая ширина колес
3.3 Величина модуля
Полученное значение согласовать со стандартом СЭВ 310-76
1 ряд: 1.5; 2.0; 2.5; 3; 4; 5;6;8;10. 2 ряд: 1.75; 2.25; 2.75; 3.5; 4.5; 5.5;7;9.
Первый ряд следует предпочитать второму 3.4 Число зубьев шестерни
Полученное значение 3.5 Уточним величину делительного диаметра шестерни и ее ширину
Желательно уточненное значение
3.6 Число зубьев колеса
Полученное значение округлить до целого числа
3.7 Окружная скорость V, (м/с)
3.8 Коэффициент торцового перекрытия
3.9 Коэффициент динамической нагрузки выбрать с учётом степени точности, окружной скорости и твердости зубьев
3.10 Определить величину коэффициента
3.11 Выполняем проверку передачи по рабочим контактным напряжениям
3.11.1 Проверка
Изменяя
3.12 Найти усилия в зацеплении колес
3.12.1 Окружная сила,
3.12.2 Радиальная сила,
3.13 Вычислить отношение
Проверочный расчет на изгибную выносливость выполняют по тому из колес пары, для которого меньше это отношение
3.14 Выполняем проверку передачи по напряжениям изгиба
3.15 Выполняем проверку передачи при перегрузках
3.15.1 По контактным напряжениям
3.15.2 По напряжениям изгиба
3.16 Геометрия передачи
3.16.1 Диаметры вершин зубьев шестерни и колеса
3.16.2 Диаметры окружностей впадин зубьев шестерни и колеса
3.16.3 Диаметры основных окружностей шестерни и колеса
3.17 Межосевое расстояние
5 Проектирование прямозубых конических передач 1 Конические передачи сложнее цилиндрических передач в изготовлении и монтаже. Для изготовления колёс требуются специальные станки и инструмент. Кроме допусков на размеры зубьев необходимо выдержать допуски на углы делительных конусов шестерни и колеса, а также на угол пересечения осей валов и при монтаже обеспечить совпадение вершин конусов. В коническом зацеплении действуют осевые силы, усложняющие конструкции опор. Всё это приводит к тому, что нагрузочная способность конической передачи составляет лишь 85% от нагрузочной способности цилиндрической. Расчёт конической прямозубой передачи выполняют через параметры эквивалентных прямозубых цилиндрических колёс. Расчёт передачи проводится по программе в табличном редакторе MICROSOFT EXCEL, что обеспечивает возможность построения диалогового режима, простоту и наглядность, а также многовариантность и оптимизацию размеров. 2 Исходные данные для расчёта
α – угол профиля исходного контура, 20°;
3 Расчёт передачи 3.1 Внешний делительный диаметр колеса de2 = 2.9 где:
3.2 Углы делительных конусов
3.3 Внешнее конусное расстояние
3.4 Ширина зуба
3.5 Модуль в внешнем торцовом сечении Полученное значение округлить до стандартного по СТ 310-76 3.6 Число зубьев колеса и шестерни
Полученные значения Z2 и Z1 округлить до целого числа. 3.7 Уточним параметры передачи 3.7.1 передаточное число 3.7.2 углы делительных конусов колеса и шестерни
3.7.3 делительные диаметры внешние шестерни и колеса
3.7.4 конусное расстояние внешнее
3.7.5 ширина зуба
3.7.6 делительные диаметры средние шестерни и колеса
3.7.7 модуль в среднем сечении
3.8 Усилия в зацеплении шестерни 3.8.1 окружная сила 3.8.2 радиальная сила 3.8.3 осевая сила 3.9 Усилия в зацеплении колеса
3.10 Окружная скорость
В соответствие с величиной скорости выбираем степень точности 3.11 Вычислить отношение (KbeU/(2-Kbe)) и уточнить величины коэффициентов KHβ, KFβ, KHV, KFV 3.12 Выполним проверку по контактным напряжениям
Если проверка не выполняется, уточняем ширину зуба
3.13 Выполним проверку по напряжениям изгиба 3.13.1 Эквивалентные числа зубьев шестерни и колеса
3.13.2 Выбрать коэффициенты формы зуба шестерни YF1 и колеса YF2 3.13.3 Если условие
выполняется, то если не выполняется 3.14 Проверка по максимальным напряжениям при перегрузке 3.14.1 по контактным напряжениям
3.14.2 по напряжениям изгиба
3.15 Геометрия передачи 3.15.1 Угол головки зуба 3.15.2 Угол ножки зуба 3.15.3 Угол конуса выступов шестерни и колеса
3.15.4 Угол конуса впадин шестерни и колеса
3.16 Внешний диаметр вершин зубьев шестерни и колеса
4 Указания к программе В таблице 2 приведён пример расчёта прямозубой конической передачи по программе с использованием табличного процессора Microsoft Excel. Для обеспечения функционирования программы в ячейки таблицы 2 следует ввести формулы в соответствии с указаниями таблицы 1 и эти ячейки с формулами защитить от изменений. Расчёт передачи ведут в следующем порядке: а) в ячейки строк 11 и 14 вводят исходные данные для расчёта; б) в ячейке F18 появляется расчётное значение внешнего модуля, которое округляется до стандартного значения и вводится ячейку A22; в) в ячейке B22 появляется расчётное число зубьев колеса, которое округляется до целого числа и вводится в ячейку C22; г) в ячейке D22 появляется расчётное число зубьев шестерни, которое округляется до целого числа и вводится в ячейку E22; д) в ячейке D34 появляется значение окружной скорости в передаче, в ячейку E34 вводят степень точности передачи, выбирают коэффициенты динамической нагрузки е) выбирают коэффициент формы зуба ж) программа выполняет проверочные расчёты по контактным напряжениям
|



 и
и  .
. ,
, - базовый предел контактной выносливости, соответствующий базовому числу циклов,
- базовый предел контактной выносливости, соответствующий базовому числу циклов,  ;
; - коэффициент долговечности;
- коэффициент долговечности; - коэффициент безопасности.
- коэффициент безопасности. ,
, - базовое число циклов нагружения;
- базовое число циклов нагружения; - эквивалентное число циклов нагружения.
- эквивалентное число циклов нагружения.
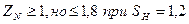
 (табл. 2)
(табл. 2)

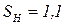

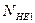 для шестерни
для шестерни ,
, - число зацеплений зуба за один оборот колеса;
- число зацеплений зуба за один оборот колеса; - один из числа действующих моментов;
- один из числа действующих моментов; - максимальный из действующих моментов.
- максимальный из действующих моментов. и
и  , можем записать в соответствии с графиком нагрузки
, можем записать в соответствии с графиком нагрузки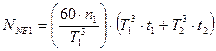

 раз меньше, т.е.
раз меньше, т.е.
 в зависимости от твердости HB
в зависимости от твердости HB

 , коэффициент долговечности
, коэффициент долговечности 



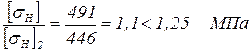
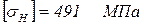



 ,
,

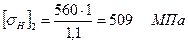

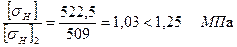
 ,
, - базовый предел выносливости по изгибу;
- базовый предел выносливости по изгибу; - коэффициент, учитывающий реверсивность нагрузки;
- коэффициент, учитывающий реверсивность нагрузки; - коэффициент долговечности;
- коэффициент долговечности;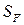 - коэффициент безопасности.
- коэффициент безопасности. (табл. 4, [3])
(табл. 4, [3])
 - для кованых колёс
- для кованых колёс - для односторонней нагрузки зуба (передача не реверсивная)
- для односторонней нагрузки зуба (передача не реверсивная) при HB<350,
при HB<350, - базовое число циклов нагружения, для всех сталей
- базовое число циклов нагружения, для всех сталей  ;
; - эквивалентное число циклов нагружения.
- эквивалентное число циклов нагружения. ,
, - показатель кривой выносливости.
- показатель кривой выносливости. .
.
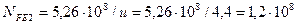
 , то принимаем
, то принимаем  .
.




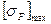 = 0.8 σt = 0.8*540=432 МПа
= 0.8 σt = 0.8*540=432 МПа  =2.8 σt=2,8* 540=1512 МПа
=2.8 σt=2,8* 540=1512 МПа
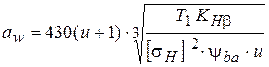
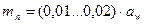

 округлить до целого числа.
округлить до целого числа.
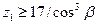


 ;
;  ;
;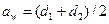

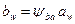
 ;
; 


 и
и 
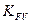


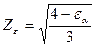




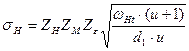
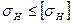 ;
; 


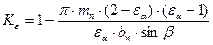







 ;
; 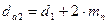
 ;
; 



 - коэффициент модуля,
- коэффициент модуля,
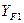 ,
, 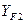 - коэффициенты формы зуба для шестерни и колеса.
- коэффициенты формы зуба для шестерни и колеса.

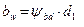




 получить примерно на (4-5)% меньше расчетного по пункту 1, что упрощает проверку по контактным напряжениям (см.п. 3.11).
получить примерно на (4-5)% меньше расчетного по пункту 1, что упрощает проверку по контактным напряжениям (см.п. 3.11).

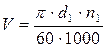


 , учитывающего суммарную длину контактных линий
, учитывающего суммарную длину контактных линий

 .
.




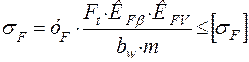





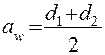
 -крутящий момент на шестерне, Н·мм:
-крутящий момент на шестерне, Н·мм: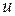 -передаточное число;
-передаточное число; допускаемые напряжения изгиба для шестерни, МПа;
допускаемые напряжения изгиба для шестерни, МПа;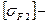 допускаемые напряжения изгиба для колеса, МПа;
допускаемые напряжения изгиба для колеса, МПа; допускаемые контактные напряжения при перегрузке, МПа;
допускаемые контактные напряжения при перегрузке, МПа; допускаемые напряжения изгиба при перегрузке, МПа;
допускаемые напряжения изгиба при перегрузке, МПа; – коэффициенты концентрации нагрузки;
– коэффициенты концентрации нагрузки; - опытные коэффициенты,
- опытные коэффициенты,  = 0,85;
= 0,85;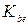 – коэффициент ширины зубчатого венца относительно внешнего конусного расстояния;
– коэффициент ширины зубчатого венца относительно внешнего конусного расстояния; - кратность моментов при перегрузке;
- кратность моментов при перегрузке;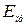 – приведённый модуль упругости, для стальных колёс 2,1·105 МПа.
– приведённый модуль упругости, для стальных колёс 2,1·105 МПа.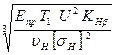 ,
,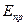 - приведённый модуль упругости материалов шестерни и колеса;
- приведённый модуль упругости материалов шестерни и колеса;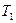 - крутящий момент на шестерне;
- крутящий момент на шестерне; - передаточное число;
- передаточное число; - коэффициент концентрации нагрузки;
- коэффициент концентрации нагрузки; - опытный коэффициент;
- опытный коэффициент; - допускаемые контактные напряжения.
- допускаемые контактные напряжения.





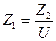












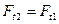 ;
;  ;
;  .
.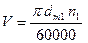
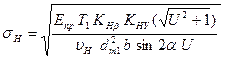 ;
; 
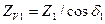
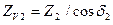

 ,
,
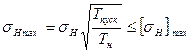

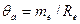

 ;
; 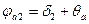

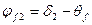
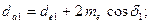

 и
и  и их значения вводят в ячейки C38 и D38, в ячейки A38 и B38 вводят значения коэффициентов концентрации нагрузки
и их значения вводят в ячейки C38 и D38, в ячейки A38 и B38 вводят значения коэффициентов концентрации нагрузки  ;
; и
и  и вводят в E42 и F42;
и вводят в E42 и F42; , напряжениям изгиба
, напряжениям изгиба  , максимальным напряжениям при пере грузке
, максимальным напряжениям при пере грузке 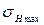 и
и  , уточняет геометрию передачи, и результаты расчёта выводит на печать.
, уточняет геометрию передачи, и результаты расчёта выводит на печать. 33
33



