
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Формирование расчетной моделиСодержание книги
Поиск на нашем сайте Работоспособность по критерию контактной выносливости рабочих поверхностей зубьев будет обеспечена при выполнении условия σн ≤ [σн]. 1.1.2.1. В основе расчетной модели определения допускаемых напряжений лежит универсальная зависимость(1.6) [σ] = а) Предельные напряжения σlim как известно зависят от параметров ФМС материалов, характера нагрузки, суммарного числа циклов напряжений в случае циклической нагрузки и конструктивных факторов. Поскольку материалы зубчатых колес, их термическая и другие обработки, параметры физико-механических свойств в проверочном расчете известны, а также очевидным является циклическая нагрузка знакопостоянного пульсирующего цикла на активные поверхности зубьев (по аналогии с поверхностью фрикционных катков, рассмотренных в лекции №3), то в качестве σlim следует принять предел выносливости при указанном цикле и соответствующем суммарном числе циклов напряжений. Суммарное число циклов контактных напряжений, физически равное количеству контактов сопряженных поверхностей за весь период эксплуатации, определяется по очевидной зависимости:
где nj – частота вращения j элемента передачи – шестерни n1, колеса n2, промежуточного (паразитного) колеса nпр (рис 2.8), Zконj – число контактов зуба j элемента одной его стороной. Методика оценки последнего параметра очевидна из рассмотрения рис.2.8. В однопоточной передаче (рис.2.1, а) число контактов для шестерни и колеса Zкон1= Zкон2=1, а для двухпоточной (с приводом от одной шестерни двух колёс (рис 2.8 б)) – Zкон1=2, Zкон2 =1. Характерно, что для зубьев передачи с паразитным (промежуточным) колесом (рис 2.8 в) Zкон1= Zкон2 = Zкон3=1. Zкон3=1 в силу того, что зубья паразитного колеса контактируют с шестерней одной стороной зуба, а с колесом − противоположной.
а) б) в)
Рис 2.8. Определение числа контактов Zконj одной стороны зуба за один оборот для зубчатых механизмов: а) однопоточного, б) двухпоточного, в) с промежуточным (паразитным) колесом
Поскольку предельные напряжения зависят от суммарного числа циклов напряжений, их следует определять для всех элементов передачи (шестерни, колеса, промежуточного колеса при наличии последнего). Значения σlim во второй и третьей зонах кривой усталости с учетом ограничений коэффициента долговечности можно определять по универсальной зависимости (1.13) σlimj = σ0j КLj = σoHlimb KHLj. (2.11) σoHlimb – международное обозначение длительного предела контактной выносливости при знакопостоянном пульсирующем цикле, величина которого зависит, главным образом, от твердости рабочих поверхностей зубьев. Например, для нормализованных и улучшенных зубчатых колес − σoHlimb = 1.8HB+65. Более подробно о предельных контактных напряжениях см. практ. занятие №3. Коэффициент долговечности по контактным напряжениям в соответствии с (1.14): KHLj = Значения базового числа циклов напряжений контактной кривой усталости NOHj лежит в диапазоне 107 б ) Допустимый коэффициент запаса по контактным напряжениям [SH ], общие соображения по назначению которого изложены в л. №3, нормирован ГОСТ 21354-87. Его значения изменяются в зависимости от материалов зубчатых колес, их термической обработки, степени опасности отказа, точности назначения нагрузки и назначаются в соответствии с рекомендациями указанного стандарта. в) Коэффициент, учитывающий конструктивно-технологические особенности проектируемой детали от образца, на котором получают опытные значения σ0Hlimb, в зубчатых передачах определяется следующим образом КК-Т.Нj = ZRjZvZxjZсм , (2.13)
где ZRj - коэффициент, учитывающий шероховатость рабочей поверхности, который назначают по шероховатости j элемента передачи; Zv – коэффициент, учитывающий окружную скорость; Zxj – коэффициент масштабного фактора j элемента передачи; Zсм – коэффициент, учитывающий влияние смазки. Числовые значения указанных коэффициентов назначаются по рекомендациям стандарта (см. практическое занятии № 3). Таким образом,
[σн]j =
1.1.2.2. В расчетной модели оценки рабочих напряжений σн прежде всего отметим то обстоятельство, что эти напряжения возникают в определённый период зацепления по любой линии контакта зубьев, лежащей в пределах активной (рабочей) их поверхности. Однако практический интерес имеют напряжения σн в той зоне, где происходит контактное выкрашивание. Напомним, что выкрашивание наблюдается на ножке зуба вблизи полюсной линии. С целью упрощения расчетов σн определяют при зацеплении в полюсе. Контактные напряжения в зубьях передачи, взаимодействующих силой Fn, моделируют сжатием двух цилиндров радиусами кривизны эвольвент в полюсе зацепления R1=ρ1 и R2=ρ2 (рис 2.9). С геометрических позиций контакт реальных зубьев и цилиндров объединяет начальный контакт по линии. Тем обстоятельством, что эвольвентные цилиндрические поверхности имеют переменные радиусы кривизны в отличие от круговых, можно пренебречь в силу малости размера hкон (рис 6.2) и плавности изменения радиуса кривизны ρ эвольвент. Далее рассмотрим возможность использования классической формулы Герца (1.23) для описания рабочих контактных напряжений с физических позиций. В этих целях сравним условия, для которых получена зависимость классической механики, с условиями работы зубчатых передач. 1.В задаче Герца цилиндры нагружены статическими сжимающими силами Fn. Поверхности зубьев, имеющих относительное перемещение, как отмечалось выше, нагружены циклически действующими силами Fn, касательной силой трения Ffr и дополнительной внутренней динамической нагрузкой, связанной с неравномерностью вращения ведомого колеса.
2. Разделительная среда между сжимаемыми цилиндрами в классической задаче не предполагалась. Зубчатые колеса в большинстве случаев работают со смазкой и между зубьями возникает разделительная масляная плёнка, существенно влияющая на процесс усталостного выкрашивания. 3.Образующие сжимаемых круговых цилиндрических поверхностей принимались параллельными, а на рабочих поверхностей зубьев реальной зубчатой передачи они имеют перекос относительно друг друга из-за неточностей изготовления, перекоса и деформации валов, износа и т. п. В общем случае для ответа на вопрос о возможности использования зависимостей классической механики или вообще зависимостей, полученных в родственных задачах, необходимо установить сколь значительно влияют на результат обнаруженные различия и при заметном влиянии найти механизмы компенсации подобных явлений. Как выше отмечено, замена сжатия двух эвольвентных цилиндрических поверхностей круговыми не вызывает серьезных изменений геометрии контакта и подобную замену принимают. Возможность перекоса образующих поверхностей контакта, а также дополнительная динамическая нагрузка могут значительно изменить величину фактических напряжений. Для компенсации этого влияния в формулу Герца вводятся коэффициенты, учитывающие неравномерность распределения нагрузки по линии контакта КНβ и дополнительную внутреннюю динамическую нагрузку Кнv. Что касается силы трения, циклического нагружения зубьев, разделительной масляной пленки, оказывающих заметное воздействия на процесс контактного выкрашивания, то их влияние учитывают при назначении допускаемых напряжений [σн]. Подобная возможность связана с тем, что предельные напряжения σ0Hlimв определяются в опыте, который проводят непосредственно на зубчатых передачах или на фрикционных катках, испытываемых с воздействием всех вышеперечисленных факторов. Таким образом, для оценки рабочих контактных напряжений можно использовать формулу Герца для начального контакта по линии (1.23): σн =
1.1.3. Получение расчетной зависимости для определения рабочих напряжений
С целью получения зависимости для технических расчетов зубчатых передач на контактную выносливость выразим все составляющие формулы Герца через исходные данные. Расчетная схема на рис. 2.10 иллюстрирует эти преобразования а) Fn – сила взаимодействия зубьев (2.5-2.6)
Fn = Ft/cosαwcosβ – колеса косозубые. Для определения окружной составляющей все исходные данные имеются. В соответствии с (2.1) Ft= 2T1/d1 =2T2/d2.
Рис. 2.10. Расчетная схема для оценки рабочих контактных напряжений: а –геометрическая и силовая модель; б, в, г – распределение нагрузки по ширине зуба (б - при строгой параллельности осей вращения и образующих активных поверхностей зубьев; в,г – в передаче, изготовленной с реальной точностью)
б) l = l∑ - суммарная длина линии контакта в зубчатых передачах, которая больше расчетной ширины зубчатых колес bw = b2 с учетом перекрытия в зацеплении (перекрытие в зацеплении указывает на одновременную передачу нагрузки двумя парами сопряженных зубьев). При этом распределение нагрузки между парами будет определяться реальной точностью изготовления передачи. Для учета отмеченного явления в расчет вводят коэффициент l∑ = bw * l∑ = где При определении суммарной длины линии контакта ширина зубчатого венца bw и угол наклона зубьев β заданы, а величина коэффициента торцевого перекрытия εα при наличии геометрических параметров определяется в соответствии с теорией эвольвентного зацепления. Отношение Fn /l∑ с физических позиций представляет собой среднюю удельную нормальную нагрузку Wn, которую можно выразить через окружную составляющую и, в конечном итоге, через заданный крутящий момент, например для прямозубой передачи:
Отношение Ft/bw = Wtср называют средней удельной окружной нагрузкой. Как отмечалось в анализе условий получения формулы Герца, эта зависимость отвечает равномерному распределению контактных напряжений по ширине катков. Подобное распределение возможно лишь в случае строгой параллельности образующих контактирующих поверхностей, к примеру так, как это показано на рис. 2.10 б. В реальной передаче имеется перекос зубчатых колес и рабочих поверхностей их зубьев относительно друг друга в начальный момент контакта на суммарный угол δ∑, включающий начальную непараллельность образующих поверхностей контакта, деформации валов и их опор и т. п. (рис. 2.10 в,). Если бы зубья были абсолютно жесткими, их контакт и передача нагрузки Ft проходили бы лишь в одной точке (рис.2.10 в). Реально упругие зубья под действием момента силы Ft начнут деформироваться и постепенно контакт должен распространиться на всю ширину зуба (применение зубчатых колес с bw, превышающей длину линии контакта – рис.2.10 г – не имеет смысла). Очевидно, что участки линии контакта, расположенные снизу на рис. 2.10 будут более деформированными и, в соответствии с законом Гука, более нагруженными. Реальное распределение удельной окружной нагрузки иллюстрируется эпюрой на этом рисунке. Из приведенных соображений следует, что увеличение длины линии контакта (ширины зубчатых колес) приводит к росту неравномерности распределения W и необходимости ограничения ширины колес. При значительных bw контакт не будет распространяться на всю ширину зуба, как это показано на рис.2.10 г. В практических расчетах ограничивают относительную ширину шестерни При определении расчетной удельной окружной нагрузки также учитывают дополнительную динамическую силу, возникающую в передаче из-за неравномерности вращения ведомого колеса. Как отмечалось выше, эту силу не рассматривают в силовом анализе, а учитывают непосредственно в прочностных расчетах с помощью коэффициента динамичности KHV. Таким образом, для прямозубой передачи:
Выше отмечена физическая природа вводимых в уравнение Герца коэффициентов
г) Приведенный радиус кривизны ρпр определяется по зависимости (
 Рис.2.11. К определению радиуса Рис.2.11. К определению радиуса
Для исключения влияния знака передаточного отношения в формулу подставляют его модуль. При этом в случае расчета мультипликаторов (повышающих передач) подставляют величину обратную передаточному отношению, т.е. 1/i. Подстановка значений
В записанной формуле кроме обозначенных выше параметров ZЕ = Zε – коэффициент, учитывающий перекрытие в зацеплении. В прямозубой передаче принимают Zε =
1.1.4. Определение коэффициента
Выше отмечалось, что степень неравномерности распределения нагрузки по длине линий контакта определяется величиной суммарного угла перекоса образующих контактирующих поверхностей относительно друг друга Таким образом, для неприрабатывающихся передач выбранной степени точности можно констатировать, что значение В прирабатывающихся зубчатых колесах может происходить полная приработка (выравнивание) удельной нагрузкой W, при которой
1.1.5. Определение коэффициента
Внутренняя динамическая нагрузка возникает в самой передаче и является результатом неравномерности вращения ведомого элемента, связанной с неизбежными погрешностями в шаге зацепления, профилях зубьев и впадин при изготовлении, а также деформациями зубьев. В основе аналитической оценки этой нагрузки лежит очевидная зависимость
Вычисление приведенного момента инерции
Здесь
где
 – окружная скорость в зацеплении, м/с – окружная скорость в зацеплении, м/с
αw – межосевое расстояние, мм. Если при расчете оказывается, что
1.2. Проектный расчет зубчатых передач на контактную выносливость активных поверхностей зубьев Исходные данные и методы их получения в проектной форме расчетов аналогичны данным проверочного расчета по пунктам 1-4 (нагрузка, кинематика, ресурс, условия эксплуатации). Задача обсуждаемого расчета заключается в определении таких геометрических параметров проектируемой передачи, которые оптимальным образом отвечают обсуждаемому критерию работоспособности. В данном случае это контактная выносливость активных поверхностей, условие которой в оптимальном случае имеет вид
В этом уравнении в соответствии с исходными данными известно лишь требуемое передаточное отношение i. Для определения коэффициента
Если в последнем случае при расчете получают Значения
где значение относительной ширины шестерни При возведении обеих частей уравнения (2.22) в квадрат и решении его относительно диаметра получим выражение
Для сокращения количества неизвестных обозначим
С учетом усредненных значений неизвестных Неизвестные При проектировании передач, нарезаемых без смещения исходного профиля, в которых
Учитывая зависимости между диаметрами делительных окружностей d1 и d2, межосевым расстоянием αw и шириной bw
уравнение (2.22) может решаться относительно любого из параметров d2, αw, и bw. В каждом отдельном случае могут использоваться проектные формулы для определения одного из указанных параметров, который для конкретной ситуации желательно получить в первую очередь. При выполнении курсового проекта можно ориентироваться на формулу (2.23). После вычисления по ней предварительного значения dw1 (d1) определяют параметр d2; aw; b1; b2; угол наклона зубьев β в косозубых и шевронных передачах, модуль зацепления m, числа зубьев шестерни и колеса z1; z2. При назначении величин m и aw следует иметь в виду, что они стандартизируются. При этом применение нормативного модуля обеспечивает использование стандартного режущего инструмента для нарезания зубьев, а округление αw до нормативного требуется лишь в случае целесообразности использования стандартизированных серийных корпусных деталей. При выполнении курсового проекта по ДМ с целью освоения методики проектирования редукторов в полном объёме серийные корпуса не используются и потому округление aw до стандартного не требуется. Вместе с тем целесообразнее назначать aw в соответствии с рядом предпочтительных чисел (как правило, по ряду R40). По мере вычисления отмеченных выше параметров уточняют предварительно принятые значения.
Лекция №10.
|
||||||||
|
Последнее изменение этой страницы: 2016-08-12; просмотров: 383; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.101 (0.011 с.) |

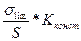 .
. , (2.10)
, (2.10)
 (2.12)
(2.12) 1.2*108 при изменении твердости рабочих поверхностей HB в диапазоне 350НВ…630НВ. В промежутке между указанными значениями твердости база испытаний NOHj = 30*HBj2.4. При вычислении КНLj значение суммарного числа циклов N∑j подставляется в случае постоянной нагрузки передачи, а эквивалентное – NEHj при переменной (см. лекцию №3).
1.2*108 при изменении твердости рабочих поверхностей HB в диапазоне 350НВ…630НВ. В промежутке между указанными значениями твердости база испытаний NOHj = 30*HBj2.4. При вычислении КНLj значение суммарного числа циклов N∑j подставляется в случае постоянной нагрузки передачи, а эквивалентное – NEHj при переменной (см. лекцию №3).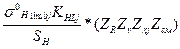 . (2.14)
. (2.14) Рис. 2.9. Моделирование контактных напряжений в зубьях с помощью сжатия круговых цилиндров
Рис. 2.9. Моделирование контактных напряжений в зубьях с помощью сжатия круговых цилиндров



 - коэффициент, учитывающий распределение нагрузки между зубьями. Для прямозубых передач перекрытие в зацеплении не велико и им обычно пренебрегают, принимая
- коэффициент, учитывающий распределение нагрузки между зубьями. Для прямозубых передач перекрытие в зацеплении не велико и им обычно пренебрегают, принимая 
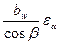
 – коэффициент торцевого перекрытия в зацеплении.
– коэффициент торцевого перекрытия в зацеплении.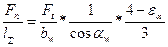
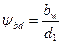 или
или  . Естественно ожидать, что первоначально контактное выкрашивание начнется в зоне действия Wtmax и именно это значение следует принять для дальнейших расчетов. Максимальное значение удельной нагрузки на эпюре можно представить как W tmax= W tср*Kβ. Kβ называют коэффициентом, учитывающим неравномерность распределения нагрузки по ширине зуба. В расчетах на контактную прочность его обозначают KHβ.
. Естественно ожидать, что первоначально контактное выкрашивание начнется в зоне действия Wtmax и именно это значение следует принять для дальнейших расчетов. Максимальное значение удельной нагрузки на эпюре можно представить как W tmax= W tср*Kβ. Kβ называют коэффициентом, учитывающим неравномерность распределения нагрузки по ширине зуба. В расчетах на контактную прочность его обозначают KHβ. . (2.17)
. (2.17) и
и 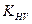 . Методы их определения раскрыты ниже.
. Методы их определения раскрыты ниже. ), в которой в соответствии с расчетной моделью ρ1 и ρ2 радиусы кривизны эвольвентных поверхностей шестерни и колеса в полюсе зацепления. Как известно, эвольвента есть кривая, очерчиваемая концом отрезка прямой при качении его без скольжения по окружности (рис. 2.11). Радиусы кривизны в точках т.1, т.2 и т. д. определяются длиной отрезка от его конца до точки касания окружности. Эвольвентные поверхности зубьев получают при обкатывании отрезков линии зацепления по основным окружностям db1 и db2. В соответствии с рис. 2.10, для прямозубых колес можно записать
), в которой в соответствии с расчетной моделью ρ1 и ρ2 радиусы кривизны эвольвентных поверхностей шестерни и колеса в полюсе зацепления. Как известно, эвольвента есть кривая, очерчиваемая концом отрезка прямой при качении его без скольжения по окружности (рис. 2.11). Радиусы кривизны в точках т.1, т.2 и т. д. определяются длиной отрезка от его конца до точки касания окружности. Эвольвентные поверхности зубьев получают при обкатывании отрезков линии зацепления по основным окружностям db1 и db2. В соответствии с рис. 2.10, для прямозубых колес можно записать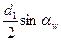 ; ρ2 =
; ρ2 =  , тогда
, тогда

 (2.17); ρпр (2.18) в исходную формулу Герца после несложных преобразований позволяет получить проверочную формулу для оценки рабочих контактных напряжений
(2.17); ρпр (2.18) в исходную формулу Герца после несложных преобразований позволяет получить проверочную формулу для оценки рабочих контактных напряжений . (2.19)
. (2.19) − коэффициент, учитывающий упругие свойства материалов сопряженных колес, который вычисляется в соответствии с (1.23):
− коэффициент, учитывающий упругие свойства материалов сопряженных колес, который вычисляется в соответствии с (1.23):  – коэффициент, учитывающий форму сопряженных поверхностей зубьев, формула для определения которого записана в универсальном виде, пригодном как для прямозубых, так и косозубых колес;
– коэффициент, учитывающий форму сопряженных поверхностей зубьев, формула для определения которого записана в универсальном виде, пригодном как для прямозубых, так и косозубых колес; ; а в косозубой – Zε =
; а в косозубой – Zε = 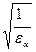 .
. (рис. 2.10 в). В свою очередь
(рис. 2.10 в). В свою очередь 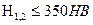 , а также окружной скорости
, а также окружной скорости  и неприрабатывающиеся – с
и неприрабатывающиеся – с 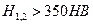 или при
или при  .
. , жесткости валов, опор и расположения зубчатых колес относительно опор, суммарной жесткости зубьев и твердости их поверхностей, характера нагрузки. Значительное количество факторов, влияющих на величину
, жесткости валов, опор и расположения зубчатых колес относительно опор, суммарной жесткости зубьев и твердости их поверхностей, характера нагрузки. Значительное количество факторов, влияющих на величину  . В проверочном расчете при определении
. В проверочном расчете при определении  .
. , учитывающего инерцию элементов, связанных с ведущим и ведомым зубчатыми колесами, а также установление точной закономерности движения механизма и значений угловых ускорений при нестационарных режимах работы, представляет достаточно сложную задачу. По этой причине более широкое распространение получил метод расчета на основе опытных данных по коэффициенту
, учитывающего инерцию элементов, связанных с ведущим и ведомым зубчатыми колесами, а также установление точной закономерности движения механизма и значений угловых ускорений при нестационарных режимах работы, представляет достаточно сложную задачу. По этой причине более широкое распространение получил метод расчета на основе опытных данных по коэффициенту  . (2.20)
. (2.20)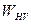 – удельная окружная динамическая сила, которая может быть вычислена так:
– удельная окружная динамическая сила, которая может быть вычислена так: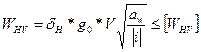 , (2.21)
, (2.21)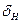 – коэффициент, учитывающий влияние вида зубчатой передачи и высотной модификации профиля головок зубьев, который определяется по таблицам (см. [ ]);
– коэффициент, учитывающий влияние вида зубчатой передачи и высотной модификации профиля головок зубьев, который определяется по таблицам (см. [ ]); – коэффициент, учитывающий разность шагов зацепления зубьев шестерни и колеса (см.[ ]);
– коэффициент, учитывающий разность шагов зацепления зубьев шестерни и колеса (см.[ ]); - межосевое расстояние, мм;
- межосевое расстояние, мм;
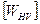 – допускаемая удельная окружная нагрузка (см [ ]);
– допускаемая удельная окружная нагрузка (см [ ]); , то ее следует принять равной допускаемому значению.
, то ее следует принять равной допускаемому значению. . С учетом зависимости (2.19) запишем
. С учетом зависимости (2.19) запишем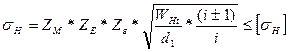 . (2.22)
. (2.22)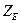 , учитывающего упругие свойства материалов зубчатых колес, а также расчетного значения допускаемых напряжений
, учитывающего упругие свойства материалов зубчатых колес, а также расчетного значения допускаемых напряжений  необходимо назначить материалы колес (см. практическое занятие №3). Значение
необходимо назначить материалы колес (см. практическое занятие №3). Значение  определяется по формуле (1.25). В качестве расчетного допускаемого напряжения
определяется по формуле (1.25). В качестве расчетного допускаемого напряжения  в прямозубой передаче принимается меньшее из значений
в прямозубой передаче принимается меньшее из значений  1,25
1,25 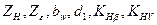 зависят от искомых размеров передачи и потому в проектном расчете являются неизвестными. При решении уравнений со значительным количеством неизвестных обычно используют метод последовательных приближений (итераций). В этом методе сначала ориентированно задаются значениями неизвестных, вычисляют требующийся параметр и по нему, в случае необходимости, корректируют значения предварительно принятых неизвестных, повторно определяя данный параметр. В соответствии с поставленной задачей уравнение (2.22) следует решать относительно геометрического параметра. В явном виде в это уравнение входят диаметр делительной окружности d1 и расчетная ширина зубчатых колес
зависят от искомых размеров передачи и потому в проектном расчете являются неизвестными. При решении уравнений со значительным количеством неизвестных обычно используют метод последовательных приближений (итераций). В этом методе сначала ориентированно задаются значениями неизвестных, вычисляют требующийся параметр и по нему, в случае необходимости, корректируют значения предварительно принятых неизвестных, повторно определяя данный параметр. В соответствии с поставленной задачей уравнение (2.22) следует решать относительно геометрического параметра. В явном виде в это уравнение входят диаметр делительной окружности d1 и расчетная ширина зубчатых колес  . С целью снижения количества неизвестных выразим
. С целью снижения количества неизвестных выразим  ,
,
 =Kd.
=Kd. и
и  при ориентировочной оценке можно принять Kd=770 – для прямозубых передач, Kd = 675 для передач косозубых и шевронных.
при ориентировочной оценке можно принять Kd=770 – для прямозубых передач, Kd = 675 для передач косозубых и шевронных. и
и  ,
,  и т.д.
и т.д. , в стандарте в окончательном виде проектная зависимость записывается так
, в стандарте в окончательном виде проектная зависимость записывается так (2.23)
(2.23)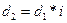 ;
;  ;
; 


