
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Особенности кинематического расчета передач трениемСодержание книги
Поиск на нашем сайте
Исходными для кинематического анализа передач трением являются частоты вращения ведущего и ведомого элементов, диапазон их изменений для передач с регулируемым передаточным отношением (устанавливаются на этапе синтеза и анализа передаточного механизма в целом (Лр. №2), а также основные геометрические размеры передач (d1; α; a1,2 и т.д.). Задача расчета заключается в определении таких кинематических параметров как окружная скорость υ, скорость скольжения υск, а также зависимости передаточного отношения и диапазона регулирования от геометрических параметров. Значения окружных скоростей υ1(2) устанавливается по известной зависимости: υ1(2) Характерной особенностью кинематики передач трением является неравенство окружных скоростей υ1 и υ2, которое обусловливается скольжением между катками или шкивами и ремнем. Скольжение разделяют на упругое и геометрическое. Упругое скольжение происходит вследствие упругих деформаций в зоне контакта веду-
щего и ведомого элементов. Рассмотрим это явление на примере контакта ремня с ведущим шкивом (рис. 10.5). При нагружении передачи моментом T1 происходит перераспределение предва- рительного натяжения ремня. В соответствии с направлением Т1 натяжение набегающей ветви F1 становится больше натяжения сбегающей ветви F2. В этом случае на набегающей ветви участок ремня длиной l при переходе его на сбегающую ветвь сократится на величину упругой деформации ∆, что повлечёт отставание ремня от шкива. Подобное отставание (скольжение) ремня будет иметь место как на ведущем, так и на ведомом шкивах. Скольжение, вызванное упругими деформациями, принято называть упругим. В качестве его оценки исполь- зуют коэффициент относительного упру- гого скольжения ε. Величина ε может быть определена как разность относительных упругих деформаций набегающей ε1 и сбегающей ε2 ветвей, вычисляемых в соответствии с законом Гука (ε = σ / Е),
где Ар - площадь поперечного сечения ремня. Так как разность (F1 - F2) зависит от величины крутящего момента Т, то очевидно, что ε = f(T). Значение ε также может быть определено из кинематических соображений. Как отмечалось выше, наличие упругого скольжения вызывает пропорциональное снижение линейных скоростей набегающей υ1 и сбегающей υ2 ветвей ремня. Разность υ1 – υ2 = υск принято называть скоростью скольжения. В относительном виде это может быть записано так
В силу пропорциональности разности линейных скоростей и относительных упругих деформаций можно записать υск / υ1 = ε и тогда условие (10.6) позволяет записать соотношение между скоростями υ1 и υ2
Полученное выражение позволяет установить зависимость передаточного отношения от геометрических параметров
Непостоянство передаточного отношения связано с отмеченной выше зависимостью ε = f(T). График этой функции показан на рис. 10.6.
Рис. 10.6. Зависимость скольжения от нагрузки в передачах трением.
На этом графике можно выделить три характерные зоны. В первой зоне нарастание скольжения с увеличением крутящего момента происходит по закону близкому к линейному, что обусловлено лишь упругими деформациями ремня с возрастанием момента до критического значения Ткр. Отклонение от линейности связано с характерными свойствами материала ремня. Что касается величины относительного упругого скольжения, то оно в ременных передачах не превышает (1,0 - 2,0) % скорости; тоже значение имеет место во фрикционных передачах с катками, футерованными упругими обкладками (резинной, например). Для стальных, чугунных катков, обладаю- щих повышенной контактной жесткостью, скольжение не превышает (0,1 - 0,2)%. При указанных значениях скольжения коэффициент относительного упругого скольжения составляет: ε ≈ 0,01 – 0,015-для плоских ремней, ε ≈ 0,015 – 0,02 - для клиновых ремней, ε ≈ 0,001 – 0,02 – для стальных и чугунных катков фрикционных передач. В связи с малостью величины ε при ориентировочных расчетах можно принимать
Cпревышением нагрузкой критического значения Ткр, соответствующего состоянию Ft= Ffr, интенсивность прироста скольжения достаточно резко увеличивается в связи с появлением геометрического скольжения (зона 2 на рисунке). Геометрическое скольжение представляет собой проскальзывание ведущего элемента относительно ведомого в силу превышения передаваемой нагрузки значения силы трения (Ft > Ffr). Увеличение интенсивности скольжения обусловливает рост относительного движения сопряженных поверхностей и их быстрое изнашивание. Дальнейшее увеличение Т может привести к чистому геометрическому скольжению (буксованию), соответствующему остановке ремня и ведомого шкива при враще- нии шкива ведущего (зона 3 на рисунке). Геометрическое скольжение также может быть связано с характерной особенностью геометрии контакта. Так, например, на рис. 10.7 показаны совмещенные эпюры окружных (линейных) скоростей контактирующей поверхностей шкива υш, являющейся переменной величиной (υш = ω × r), и боковой контактирующей поверхности ремня υp. Как из рисунка, лишь в одной точке поверхности контакта скорости совпадают. Выше этой точки поверхность шкива опережает поверхность ремня, а ниже - отстает от нее. Максимальную разность скоростей υш – υр используют в качестве количественной оценки геометрического скольжения. Очевидно, что для снижения геометрического скольжения требуется уменьшение толщины ремня, что ограничивается величиной передаваемой нагрузки. Аналогичные явления могут иметь место и во фрикционных передачах (см. наложения эпюр υ1 и υ2 на рис. 10.2). В кинематике передач трением с плавно регулируемой скоростью ведомого элемента (вариаторов) выделяют максимальное и минимальное передаточное отношение. Очевидно, что для ориентировочной их оценки без учета скольжения применительно к механизму, показанному на рис.10.2, можно записать
Кроме того для вариаторов выделяют понятие диапазона регулирования Д, характеризующего соотношение граничных значений регулируемого параметра (в рассматриваемом случае – частоты вращения ведомого вала) Дш = nmax / nmin. С учетом значений n2max и n2min в соответствии с (10.9) и (10.10) можно записать
Применительно к вариатору, показанному на рис. 10.2., в котором ведущий каток может быть перемещен к оси вращения ведомого, d2min = 0, а Д = ∞. На практике диапазон регулирования простейших механизмов с варьированием радиусов одного из элементов
Рис. 10.5.
(ведущего или ведомого) не превышает 2 - 3. Ограничение Д применительно к обсуж- даемому вариатору связано с возрастанием геометрического скольжения в зоне малых значений d2. Это обстоятельство иллюстрирует рис. 10.8., на котором показаны векторы ок- ружных скоростей для ведущего и ведомого элементов на совместной площадке их кон- такта в положениях 1 и 2. Как видно из со- поставления положений векторов υ1 и υ2 относительно друг друга, при приближении к оси вращения ведомого катка значительно увеличится угол δ. Физически это означает, что поверхности ведущего и ведомого эле- ментов в исследуемой точке контакта дви- жутся в разных направлениях, скользя отно- сительно друг друга. Интенсивный износ поверхностей трения обоих элементов в этом случае заставляет предусматривать раз- личные ограничители, исключающие работу в заштрихованной на рисунке зоне.
|
||
|
Последнее изменение этой страницы: 2016-08-12; просмотров: 258; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.102 (0.007 с.) |

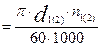 , м/с. (10.4)
, м/с. (10.4) Рис. 10.5. К характеристике упругого скольжения в ремённой передаче.
Рис. 10.5. К характеристике упругого скольжения в ремённой передаче. . (10.5)
. (10.5) 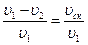 . (10.6)
. (10.6)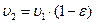 . (10.7)
. (10.7) (10.8)
(10.8)
 .
. Рис. 10.5. Геометрическое скольжение, связанное с особенностями геометрии контакта.
Рис. 10.5. Геометрическое скольжение, связанное с особенностями геометрии контакта. , (10.9)
, (10.9) . (10.10)
. (10.10) (10.11)
(10.11)



