
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Определение момента инерции тела методом крутильных колебанийСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Цель работы: определение момента инерции диска. Приборы и принадлежности: кронштейн с закрепленной проволокой, испытуемое тело, два цилиндра, секундомер, штангенциркуль.
Краткая теория
Основными характеристиками динамики вращательного движения являются: момент инерции и момент силы. Момент инерции – есть мера инертности тела, имеющего ось вращения. Во вращательном движении момент инерции имеет такую же роль, как масса при поступательном движении. Как и масса момент инерции (относительно оси вращения) скалярная величина. Однако величина момента инерции тела зависит от положения оси вращения. Момент инерции материальной точки относительно оси вращения, находящейся на расстоянии r, равен произведению массы на квадрат расстояния до оси вращения Момент инерции твердого тела равен сумме моментов инерции его составных точек Момент инерции относительно произвольной оси, не проходящей через центр масс, можно вычислить по теореме Штейнера.
I=Io+ma2. (1)
Момент силы – величина векторная, численно равная произведению силы на плечо
Плечом называется кратчайшее расстояние от оси вращения до линии действия силы ( рис.2). Момент силы и момент инерции связаны соотношением:
где ε – угловое ускорение. Это есть основное уравнение динамики для вращательного движения.
Применим к этим колебаниям основное уравнение вращательного движения. При крутильных колебаниях на тело действует возвращающий момент со стороны нити подвеса, обусловленный упругими силами.
тогда
Полученное уравнение является дифференциальным уравнением крутильных колебаний, в этом уравнении отношение D/I = w2 – циклическая частота – ω.
Вывод рабочей формулы. Воспользуемся методом крутильных колебаний для определения момента инерции диска, подвешенного на упругой нити (рис.4). Для этого используем формулу периода крутильных колебаний. Однако в этой формуле две неизвестные величины: I – момент инерции диска относительно оси О, проходящей через центр масс диска, и D – модуль упругости нити. Учитывая аддитивные свойства момента инерции, поставим на диск два груза и запишем второе уравнение
где I a – момент инерции двух грузов относительно оси О. Возведем (5,6) в квадрат и разделим одно уравнение на другое:
Выразим момент инерции диска
Момент инерции двух грузов относительно оси О по теореме Штейнера равен:
где I 0 – момент инерции цилиндра относительно его оси, проходящей через центр масс. Подставим полученное выражение в предыдущую формулу и получим:
где r – радиус цилиндра, a – расстояние между осями диска и цилиндра. Выражение (7) является рабочей формулой для расчета момента инерции диска. Выполнение работы 1. Запустите крутильные колебания и дайте им установиться, измерьте время t заданного числа колебаний. Найдите период колебаний диска без грузов 2. Поставьте на диск одновременно цилиндры, измерьте время t1 и период T1 с грузами. 3. По рабочей формуле рассчитайте момент инерции диска.
Расчет погрешности
Абсолютная ошибка измерения момента инерции вычисляется по формуле:
ΔT=ΔT1 =0,01 c Δа= Δr =1мм
Задачи 1. Определите момент инерции сплошного однородного диска радиусом R =40 см и массой m =1 кг относительно оси, проходящей через середину одного из радиусов перпендикулярно плоскости диска. Ответы: 1) 0,22 кг.м2; 2) 0,12 кг.м2; 3) 0,32 кг.м2; 4) 0,08 кг.м2; 5) 0,28 кг.м2. 2. Определите момент инерции тонкого однородного стержня длиной ℓ=50 см и массой m =360 г относительно оси, перпендикулярной стержню и проходящей через конец стержня. Ответы: 1) 3.10–2 кг.м2; 2) 1,8.10–2 кг.м2; 3) 2,6.10–2 кг.м2; 4) 1,3.10–2 кг; 5) 2,8.10–2 кг.м2.
3. Твердое тело совершает крутильные колебания на упругой нити. Чему равен модуль упругости нити, если момент инерции тела I =1,12.10–2 кг.м2, а период колебаний 4,35 с? Ответы: 1) 2,15.10–1Дж; 2) 3, 85.10–2Дж; 3) 2,33.10–2Дж; 4) 1,23.10–1Дж; 5) 2,95.10–2Дж. 4. К ободу колеса, имеющего форму диска, радиусом 0,5 м и массой m=50 кг приложена касательная сила 98,1 Н. Найти угловое ускорение колеса. Ответы: 1) 5,82 рад/с2;2) 7,8 рад/с2; 3) 4,53 рад/с2; 4) 8,5 рад/с2; 5) 3,52 рад/с2. 5. Определите момент инерции тонкого однородного стержня длиной ℓ=50 см и массой m=360 г относительно оси, перпендикулярной стержню и проходящей через точку, отстоящую от конца стержня на 1/6 его длины: Ответы: 1) 2,27.10–2 кг.м2; 2) 2,8.10–2 кг.м2; 3) 2,15.10–2 кг.м2; 4) 1,75.10–2 кг.м2; 5) 3,30.10–2 кг.м2. 6. Однородный диск радиусом R=0,2 м и массой m=5 кг вращается вокруг оси, проходящей через его центр. Зависимость угловой скорости вращения диска от времени дается уравнением ω=А+Вt, где В=8рад/с2. Найти величину касательной силы, приложенной к ободу диска. Ответы: 1) 2,3 Н; 2) 5,3 Н; 3) 4 Н; 4) 4,8 Н; 5) 1,23 Н.
1. Цель работы. 2. Вывод рабочей формулы. 3. Физический смысл момента инерции твердого тела и материальной точки. 4. Теорема Штейнера. 5. Где при выводе рабочей формулы использовалась теорема Штейнера? Когда применяется эта теорема? 6. Основное уравнение динамики вращательного движения. 7. Вывод дифференциального уравнения крутильных колебаний. 8. Момент силы. Направление момента силы.
Литература
1. Савельев И. В. Курс общей физики, т. 1. М.: Наука, 1989. с.104–108. 2. Трофимова Т. И. Курс физики. М.: Высшая школа, 2002, с.36–38. 3. Бондарев Б. В., Спирин Г. Г., Калашников Н. П. Курс физики. М.: Курс общей физики, 2003, т.1, с.191–194. Лабораторная работа 1.6
Измерение ускорения силы тяжести с помощью оборотного маятника
Приборы и принадлежности: оборотный маятник, секундомер, линейка, опорная призма.
Краткая теория
Физический маятник – твердое тело, которое совершает колебания вокруг горизонтальной оси, не проходящей через центр масс (рисунок). В положении равновесия вращающий момент силы тяжести равен нулю, так как плечо этой силы равно нулю. При отклонении от положения равновесия на угол j (рисунок) возникает вращающий момент, равный
При малых углах (j»50) sinj»j и тогда
Минус означает, что вращающий момент стремится вернуть маятник в положение равновесия. Из основного уравнения динамики вращательного движения вращающий момент
Выражение (3) называют дифференциальным уравнением колебаний физического маятника. В этом уравнении собственная циклическая частота колебаний физического маятника равна
Если в формуле (4) вместо выражения
где Точка, лежащая на прямой, проведенной через точку подвеса В1 и центр тяжести С, на расстоянии приведенной длины
Точка подвеса В1 и центр качания В2 являются взаимозаменяемыми. Если маятник подвесить за центр качания или за точку подвеса, то периоды колебаний не изменятся. На этом свойстве основано измерение ускорения силы тяжести с помощью оборотного маятника (рис.1). Следует отметить, что при небольших смещениях подвижного груза М маятника, можно принять почти линейной зависимость периода колебаний маятника от положения груза.
Порядок выполнения работы Оборотный маятник представляет собой две параллельные друг другу, закрепленные вблизи его концов, опорные призмы В 1и В 2, за которые он может поочередно подвешиваться. Вдоль стержня маятника может перемещаться груз М. Для выполнения работы следует: 1. Получить два значения для положения груза М (2–13 см). 2. Пользуясь секундомером, определить периоды колебаний маятника на призмах В 1 и В 2, когда груз М находится в первом и втором положениях. По формуле 3. Полученные значения периодов поставить на графике, по оси ординат отложить период, а по оси абсцисс положение груза М (х). Соединить точки для периодов при первом положении и при втором положении груза М (х). 4. Установить положение груза в точку пересечения прямых. 5. Определить период колебаний, когда маятник висит на призме В 1– 6. Измерить расстояние между призмами, которое равно приведенной длине маятника 7. Используя периоды колебаний 8. Заполнить таблицу.
Расчет погрешности
Относительная погрешность:
абсолютная погрешность:
Задачи
1. Тонкий обруч, повешенный гвоздь, вбитый горизонтально в стену, колеблется в плоскости параллельной стене. Радиус обруча R=30 см. Вычислить период колебаний.
Ответы: 1) 1,35 с; 2) 1,55 с; 3) 2,32 с; 4) 1,95 с; 5) 1,21с. 2. Диск радиусом R =24 см колеблется около горизонтальной оси, проходящей через середину одного из радиусов перпендикулярно плоскости диска. Определить приведенную длину такого маятника. Ответы: 1) 53,2 см; 2) 63,5 см; 3) 24,4 см; 4) 36 см; 5) 43,2 см. 3. Однородный стержень длиной 1 м и массой 0,5 кг вращается в вертикальной плоскости вокруг горизонтальной оси, проходящей через середину стержня. С каким угловым ускорением вращается стержень, если вращающий момент равен 9,81.10–2 Н.м? Ответы: 1) 23,5.10–2 рад/с2; 2) 18,3.10–2 рад/с2; 3) 1,2.10–1 рад/с2; 4) 32,5.10–2 рад/с2; 5) 3,12.10–1 рад/с2. 4. Обруч диаметром 56,5 висит на гвозде, вбитом в стену и совершает колебания в плоскости, параллельной стене. Найти период этих колебаний. Ответы: 1) 2,32 с; 2) 1,50 с; 3) 1,85 с; 4) 2,02 с; 5) 1,38 с. 5. Чему равен период колебаний математического маятника на Земле длиной 1м? Ответы: 1) 5,38 с; 2) 3,04 с; 3) 2,88 с; 4) 3,56 с; 5) 4,01 с. 6. Маховик, момент инерции которого I = 63,6 кг/м2, вращается с постоянной угловой скоростью ω =31,4 рад/с. Найти тормозящий момент М, под действием которого маховик останавливается через 20 с. Ответы: 1) 100 Нм; 2) 200 Нм; 3) 150 Нм; 4) 230 Нм; 5) 99,8 Нм.
Контрольные вопросы
1. Что называется физическим маятником? 2. Что называется осью вращения и осью качения? 3. Что называется математическим маятником? 4. Какой маятник называется оборотным? 5. Что называется приведенной длиной физического маятника? 6. Запишите дифференциальное уравнение физического маятника? 7. Как определить положение подвижного груза, чтобы расстояние между призмами стало равно приведенной длине физического маятника? 8. Ход работы.
Литература
1. Бондарев Б. В., Спирин Г. Г., Калашников Н. П. Курс физики. М.: Курс общей физики, 2003, т.1, с.205. 2. Детлаф А. А., Яворский Б. М. Курс физики, М.: Высшая школа, 1989, с.300–302.
Лабораторная работа 1.7
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-08; просмотров: 3858; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.191.212.181 (0.01 с.) |

 .
. . В случае непрерывного тела момент инерции тела относительно заданной оси представится выражением
. В случае непрерывного тела момент инерции тела относительно заданной оси представится выражением  .
.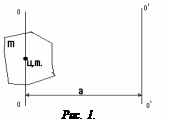 Момент инерции относительно произвольной оси равен сумме момента инерции тела относительно оси, проходящей через центр масс, параллельно заданной оси и произведению массы на квадрат расстояния между осями ( рис.1).
Момент инерции относительно произвольной оси равен сумме момента инерции тела относительно оси, проходящей через центр масс, параллельно заданной оси и произведению массы на квадрат расстояния между осями ( рис.1).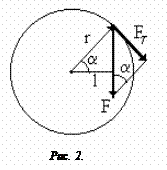
 . (2)
. (2) ,(3)
,(3) Крутильные колебания – это такие колебания, которые совершает подвешенное твердое тело вокруг вертикальной невесомой упругой нити, верхний конец которой закреплен (рис.3).
Крутильные колебания – это такие колебания, которые совершает подвешенное твердое тело вокруг вертикальной невесомой упругой нити, верхний конец которой закреплен (рис.3). и
и  ,
,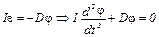 ,
, . (4)
. (4) . (5)
. (5) , (6)
, (6) ,
,  ,
,  .
. .
. ,
, , (7)
, (7) , где N – число колебаний.
, где N – число колебаний.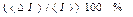



 Контрольные вопросы
Контрольные вопросы . (1)
. (1)

 . (2)
. (2) , подставив в (2), получим
, подставив в (2), получим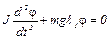 . (3)
. (3) . Период колебаний физического маятника
. Период колебаний физического маятника . (4)
. (4)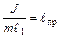 подставим
подставим  , то получим формулу для периода математического маятника
, то получим формулу для периода математического маятника , (5)
, (5) определить периоды колебаний
определить периоды колебаний  ,
,  ,
,  ,
,  где n – число колебаний маятника (задается преподавателем),
где n – число колебаний маятника (задается преподавателем),  – период колебаний, когда груз М маятника находится в первом положении, а маятник висит на призме В 1,
– период колебаний, когда груз М маятника находится в первом положении, а маятник висит на призме В 1,  – период колебаний, когда груз М маятника находится во втором положении, а маятник висит на призме В 2.
– период колебаний, когда груз М маятника находится во втором положении, а маятник висит на призме В 2. , и определите период колебаний, когда маятник висит на призме В 2–
, и определите период колебаний, когда маятник висит на призме В 2– 


 ,
с
,
с
 ,
с
,
с
 ,
с
,
с





