Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Неинерциальные системы отсчетаСодержание книги
Поиск на нашем сайте
Сейчас предпологжим, что в K0, движущейся прямолинейно и равномерно, тело также движется прямолин. и равномерн., а сист. отсчета K’ движется относит. K0 ускоренно. Тогда по отнош. к сист. K’ тело движется с некоторым ускорением и в этом случае не соблюдается принцип инвариантности Галилея. Сист. отсчета K’ явл. неинерциальной по отнош. к отнош. K0. На рис. Показаны векторы Тогда Поскольку движение системы отсчета K’ по отношению к K0 ускоренное, то выр. 1 мы можем диф-ть по времени, и продиф-вав его дважды мы получим равенство Тогда ур-ние 2 запишется в виде
Колебание. Типы колебаний Колебаниями наз. движения или процессы, обладающие то или иной повторяемостью во времени. Колебания м.б. разной природы. В класс. физике рассм. механические, электромагн. и электромех. колебания. В зависимости от характера воздействия на колеблющуюся сист. различают: свободные, или собственные колеб.; автоколеб. и параметрические колебания. Свободными наз. колеб., кот. происходят в отсутствие внешних переменных воздействий на колебат. сист. и возникают вследствие какого-либо начального отклонения этой сист. от состояния ее устойчивого равновесия. Вынужденными наз. колеб., возникающие в какой-либо системе под влиянием переменного внешнего воздействия. Автоколебаниями наз. колеб., кот. задается внешней силой, а сама система, на кот. действует эта сила, управляет этой внешней силой. Параметрические - колеб, кот. происходят за счет внешних сил, периодически изменяющих какой-либо параметр системы (напр. изменение длины нити маятника). Колеб. наз. периодич., если значения всех физ. величин, хар-щих колеб. Систему и изменяющихся при ее колебаниях, повторяются через равные промежутки времени. Наименьший промежуток времени Т, удовлетворяющий этому условию, наз. периодом колебаний. За период колеб. Т система совершает одно полное колебание. Частотой периодич. колебаний наз. величина Циклической, или круговой частотой, периодич. колеб. наз. величина
Гармонические колебания При периодич. колеб. зависимость колеблющейся величины S от времени t удовлетворяет условию S(t+T)=S(t). Периодич. колеб. величины S(t) наз. гармоническими колебаниями, если величина S(t) совершает колебания по закону синуса или косинуса. Значение S(t) в произвольный момент времени t опред. значением фазы колебаний Ф(t)= Запишем гармонич. колебание в виде уравнения S(t)=Asin( Начальная фаза скорости = Начальная фаза ускорения равна
Если гармонически колеблющаяся величина Общее реш. этого ДУ приводится к стандартному виду гармонич. колеб.
Метод вект. диаграмм Гармонич. колеб. можно изобразить графически в виде вектора на плоскости. Для этого из нач. коорд. т.О на плоскости проводят вектор Графическое изображение гармонич. колебаний посредствам вращающегося вектора амплитуды наз. методом векторных диаграмм. Этим методом широко пользуются при сложении одинаково направленных гармонич. колеб.
|
||
|
Последнее изменение этой страницы: 2016-12-12; просмотров: 409; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.156 (0.006 с.) |

 В преобразованиях Галилея предполагается, что система отсчета K’ движется относительно системы K0 прямолинейно и равномерно. В этом случае как система K0, так и K’ явл. инерциальными.
В преобразованиях Галилея предполагается, что система отсчета K’ движется относительно системы K0 прямолинейно и равномерно. В этом случае как система K0, так и K’ явл. инерциальными.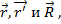 связывающих тело в этих 2-х сист. отчета.
связывающих тело в этих 2-х сист. отчета.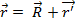 (1), где
(1), где  - радиус-вектор частицы в сист. отсчета K’;
- радиус-вектор частицы в сист. отсчета K’;  - //- K0 ;
- //- K0 ; 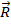 - радиус-вектор, определяющий начало координат системы K’ по отношению к сист. отсчета K0.
- радиус-вектор, определяющий начало координат системы K’ по отношению к сист. отсчета K0.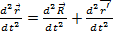 (2).
(2). 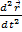 , равная
, равная 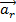 , есть ускорение частицы в системе K0.
, есть ускорение частицы в системе K0. 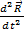 , равная
, равная 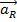 , есть ускорение начала координат O’ системы K’ по отношению к K0. В случае поступат. движ. частицы,
, есть ускорение начала координат O’ системы K’ по отношению к K0. В случае поступат. движ. частицы,  даст ускорение частицы в системе K’ и равна
даст ускорение частицы в системе K’ и равна 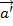 .
.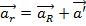 . Умножим это выр. на массу частицы m, перегруппировав, получим
. Умножим это выр. на массу частицы m, перегруппировав, получим 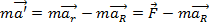 , т.е. по сравнению с инерц. сист. отсчета, в кот. действует 2-й зак. Ньютона, в неинерц. сист. возникает дополнительная сила
, т.е. по сравнению с инерц. сист. отсчета, в кот. действует 2-й зак. Ньютона, в неинерц. сист. возникает дополнительная сила 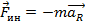 , кот. наз. силой инерции.
, кот. наз. силой инерции.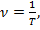 равная числу полных колебаний, совершающихся за единицу времени.
равная числу полных колебаний, совершающихся за единицу времени.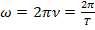 и равная числу полных колебаний, совершаемых за
и равная числу полных колебаний, совершаемых за  единиц времени.
единиц времени.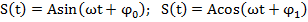 , где величина A = Smax=const >0 есть мах значение колеблющ. величины S и наз. амплитудой коелбаний,
, где величина A = Smax=const >0 есть мах значение колеблющ. величины S и наз. амплитудой коелбаний,  и
и 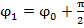 постоянные величины.
постоянные величины.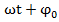 ; Ф1(t)=
; Ф1(t)= 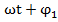 величин
величин 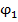 представляют собой начальные фазы колебаний, т.е. значение Ф(t) и Ф1(t) в момент времени t=0 начала отсчета времени
представляют собой начальные фазы колебаний, т.е. значение Ф(t) и Ф1(t) в момент времени t=0 начала отсчета времени 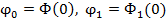 .
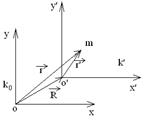
.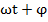 ), где S(t) – величина смешения м.т. из положения равновесия, тогда 1-я и 2-я произв., т.е v и a колеблющегося тела запишется в виде формулы
), где S(t) – величина смешения м.т. из положения равновесия, тогда 1-я и 2-я произв., т.е v и a колеблющегося тела запишется в виде формулы 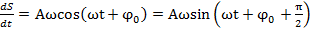 ;
; 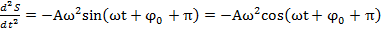 , причем амплитуды скорости и ускорения соответственной равны
, причем амплитуды скорости и ускорения соответственной равны 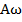 и
и 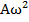 .
.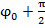 , т.е разность фаз колебаний скорости и смешение S(t) постоянны и =
, т.е разность фаз колебаний скорости и смешение S(t) постоянны и =  . Это значит, что величина
. Это значит, что величина 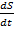 опережает S(t) по фазе на
опережает S(t) по фазе на 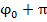 , т.е. разность фаз. Колебаний ускорения и S(t) постоянна и =
, т.е. разность фаз. Колебаний ускорения и S(t) постоянна и = 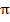 .
.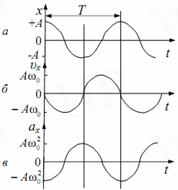 Графики зависимости величин S (а),
Графики зависимости величин S (а), 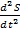 (в) для гармонических колебаний в случае
(в) для гармонических колебаний в случае 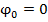 показаны на рис. (S(t)=Acos….).
показаны на рис. (S(t)=Acos….). ,
,  , то гармонически колеблющаяся величина S(t) удовлетворяет ДУ типа
, то гармонически колеблющаяся величина S(t) удовлетворяет ДУ типа 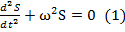 .
.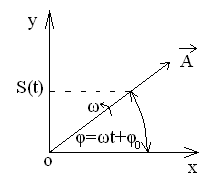
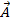 , модуль кот. = амплитуде A рассматриваемых колебаний и составляет с осью координат Ох угол
, модуль кот. = амплитуде A рассматриваемых колебаний и составляет с осью координат Ох угол 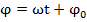 , т.е. = фазе колебаний в данный момент времени. С теч. времени t угол
, т.е. = фазе колебаний в данный момент времени. С теч. времени t угол 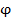 увелич. так, что вектор
увелич. так, что вектор 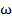 . Тогда проекция
. Тогда проекция