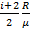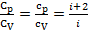Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Число степеней свободы.Внутренняя энергия газаСодержание книги
Поиск на нашем сайте Совершая беспорядочное тепловое движение, молекулы приобретают ср. кинетич. эн. поступат. движ. Где Т.к. Для идеального газа кинетич. энергия беспорядочного движения всех его молекул определяет его внутреннюю энергию. Кинетич. эн. поступат. движ. вносит основной вклад в энергию беспорядочного движения молекул, хотя свой вклад вносит также кинетич. эн. вращения и колебания молекул. Для того, чтобы подсчитать энергию, идущую на все виды движения молекул, вводится понятие о числе степеней свободы. Под числом степеней свободы тела подразумевается число независимых координат, которые необходимо ввести для определения положения тела в пр-ве. Напр. м.т. обладает 3-мя степенями свободы, т.к. ее положение в пр-ве ПДСК задается 3-мя координатами x,y,z. Положение тв. тела мы определим, если зададим: 1)положение его центра тяжести в пр-ве; 2)направление некоторой опред. оси ОО'; 3)угол поворота этого тела вокруг оси ОО' по отношению в некоторому нач. положению тела. Для определения положения центра тяжести нужно ввести 3 координаты x,y,z. Для определения направления оси ОО' в пр-ве надо задать еще 2 координаты, напр. 2 угла Угол поворота тела вокруг оси ОО' определяется еще одной координатой, напр. угол Основной предпосылкой МКТ явл. предположение о полной беспорядочности движения молекул. Ни один из типов движения не имеет преимущества перед другими, из чего следует, что на каждую степень свободы молекулы в среднем приходится одно и то же кол-во энергии Это предположение представляет собой положение о равнораспределении энергии по степеням свободы. На поступат. движ. молекулы, которому соответствует 3 степени свободы, приходится энергия Если отнести внутр. эн. к 1 молю газа, то полный запас внутр. энергии газа, содержащего n молекул, равен
Теплоемкость газов Пользуясь представлением о внутр. эн., найдем выражение для теплоемкости газов. Под удельной теплоемкостью «с» какого-либо вещества понимаю физ. величину, численно равную кол-ву тепла, которое необходимо сообщить единице массы этого вещества, чтобы поднять ее температуру на Под молярной теплоемкостью «С» какого-либо вещества подразумевается физ. величина, численно равная кол-ву тепла, которое надо сообщить 1 молю этого вещества, чтобы поднять его температуру на
Молекулярная теплоемкость газа при пост. объеме V СV численно равна изменению внутр. энергии одного моля газа
Тогда удельная теплоемкость «с» -с V= При нагревании газа при пост. давлении P газ расширяется, сообщенное ему извне тепло идет на увеличение запаса внутренней энергии U и на совершение работы A против внешних сил. Таким образом, СP больше теплоемкости СV на ту работу A, которую совершает 1 моль газа при расширении, происходящем в рез-те повышения температуры на СP = СV + A Оказывается, что искомая работа A равна газовой постоянной R. СP = СV + R, или через степень свободы СP = Тогда удельная теплоемкость СP равна с p= с V + И отношение
|
||
|
Последнее изменение этой страницы: 2016-12-12; просмотров: 320; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.156 (0.007 с.) |

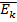 при температуре T, равную
при температуре T, равную 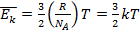 ,
, - газовая постоянная;
- газовая постоянная;  – число Авогадро;
– число Авогадро;  - пост. Больцмана
- пост. Больцмана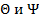 , которые она составляет с 2-мя из 3-х координатных осей.
, которые она составляет с 2-мя из 3-х координатных осей. , т.е. тв. тело обладает 6-ю степенями свободы (x,y,z
, т.е. тв. тело обладает 6-ю степенями свободы (x,y,z 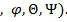
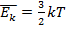 или для газа, состоящего из одинаковых молекул
или для газа, состоящего из одинаковых молекул 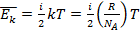 , где
, где 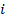 - число степеней свободы.
- число степеней свободы.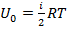 .
.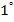 .
. , где
, где 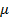 – молекулярный вес данного вещества.
– молекулярный вес данного вещества.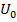 при повышении его температуры на
при повышении его температуры на  , СV=
, СV= 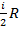 .
. .
.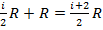
 или с p =
или с p =